|
«Решение простейших тригонометрических уравнений»
    
Муниципальное бюджетное общеобразовательное учреждение
Средняя общеобразовательная школа № 62 хутора Павловского Крымского района Краснодарского края.
Методическая разработка урока
по алгебре и началам анализа в 10 классе
по теме:
Решение простейших тригонометрических уравнений
Зозуля Татьяна Николаевна
учитель математики
2014 год
Тема: «Решение простейших тригонометрических уравнений»
Участники: учащиеся 10 класса
Тип урока: урок разноуровнего повторения, с показом презентации.
Форма урока: Фронтальный опрос, дифференцированный опрос, фронтальное обсуждение, работа с разноуровневыми группами.
Цель:
Задачи урока:
образовательные:
формирование умения решать простейшие тригонометрические уравнения.
закрепление навыков решения уравнений на уравнениях В и С уровня сложности.
развивающие:
развитие умения анализировать и делать выводы о способе решения уравнений содержащих дробный , отрицательный, сложный аргумент
развитие самостоятельности, ответственности, творческого отношения к деятельности
активизация внимания учащихся с помощью интерактивных средств обучения
воспитательные:
Оборудование: мультимедийное оборудование, компьютер у учителя, интерактивная доска, набор кликкеров 7шт.,индивидуальные карточки с тестами, рабочие листы- памятки для учащихся .
Ход урока
Этапы урока
|
Содержание
|
1.Орг. момент.
Рефлексия.
2. Сообщение темы, задач урока
3.Повторение
4.. Изучение нового материал
5. Промежуточный контроль
6.Изучение нового материала.
7.Промежуточный контроль
8.Создание проблемной ситуации (для группы С)
9.Закрепление изученного материала.
10. Подведение итогов урока.
11.Домашнее задание.
|
(Слайд№1) Посмотрите на экран. Включите воображение и эмоции. Какое первоначальное чувство вызывает это изображение? Главное это беспредельная высота и чистота. Приятная зелень родной земли и свободный полет яркой бабочки. Я хочу и надеюсь, что такие же чувства свободного полета, стремления ввысь, чистоты и радости, умиротворения и восторга будут вызывать у вас самостоятельно найденное верное решение, интересная мысль, удовлетворение от достижения целей. Счастливого полета!
(Слайд№1) Сегодня на уроке мы проведем обобщающее повторение решения простейших тригонометрических уравнений. Вспомним 1)основные формулы для решения тригонометрических уравнений: sint=a; cost=a; tgt=a; ctgt=a.
2)Рассмотрим уравнения содержащие более сложный аргумент.
3)Увидим ,что тригонометрическое уравнение должно быть приведено к виду, содержащему лишь одну тригонометрическую функцию одного аргумента.
(Слайд№2) Определите знак выражения, объявляя какой четверти, принадлежит угол.
sin200;cos ;tg140;ctg290;sin ;tg140;ctg290;sin . .
(Cлайд№3) Упростите выражение:
sin(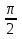 – t);cos(2 – t);cos(2 + t); tg( + t); tg( -t); ctg(180- t); sin(270-t) -t); ctg(180- t); sin(270-t)
(Слайд№4) При помощи интерактивной доски учащиеся должны найти и исправить ошибку.
arccos(- ) = - ) = - 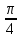 ; arcsin ; arcsin = =  ; arcsin(- ; arcsin(- 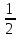 ) = ) =  ; arctg ; arctg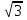 = не существует; arctg(- 1) = = не существует; arctg(- 1) = 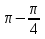
(за шторкой как подкрепление к решению расположены формулы нахождения обратной тригонометрической функции с отрицательным аргументом)
Демонстрация слайдов №6; №7; №8( решение уравнения cost=a)
Уровень А
|
Уровень В
|
Уровень С
|
Решение заданий с комментарием и последующей проверкой с использованием интерактивной доски.
(приложение 2)
1)cosx= , ,
x= +2 +2 . .
|
Решение за крылом доски
(приложение 2)
1)cos(2x - )- )- 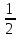 = 0 = 0
cos(2x - ) = ) = 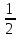
2x- = = 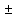  +2 +2
2x=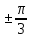 + +  +2 +2
x= + +  + +
|
Решение за крылом доски
(приложение 2)
1)cos 2x- sin²2x= 2x- sin²2x=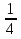
cos4x=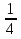
4x =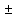 arccos arccos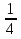 +2 +2
x= arccos arccos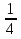 + +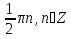
|
2)cos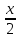 =0, =0,
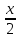 = =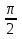 + +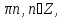
x= +2 +2 n n Z. Z.
|
2)cos(2x +  )– 1=0 )– 1=0
2x + = 2 = 2
2x = -  +2 +2
x = -  + +
|
2)4(1-cosx)+cos²x = 0
4-4cosx+cos²x=0
(2-cosx)²=0
2-cosx=0
cosx=2
нет корней
|
3)2cosx=1,
cosx =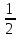 , ,
x=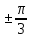 +2 +2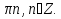
|
3)4cos 6x= -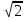
cos 6x = - 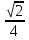
6x=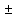 ( ( -arccos -arccos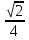 ) +2 ) +2
x=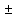  ( ( -arccos -arccos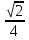 ) + ) +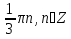
|
3)|cosx|=
cosx=
x=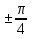 + +
|
Демонстрация слайдов№9,№10,№11;12;13(решение уравнения sint=a; tgx=a). Сказать об уравнении ctgx = a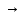 tgx = tgx = 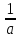 ,a ,a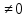
Уровень А
|
Уровень В
|
Уровень С
|
4)sinx= - , ,
x= + +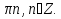
5)tg(-3x)=1,
x= - + +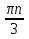 ,n ,n . .
|
4)4sin6x=-2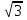
sin6x= -
6x= + +
x= + +
|
4)4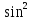 x-5|sinx|+1=0 x-5|sinx|+1=0
|sinx|=t, 0
4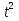 -5t+1=0 -5t+1=0
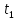 =1, =1, = =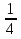
sinx=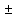 1,sinx= 1,sinx=
x=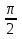 + +
x=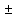 arcsin arcsin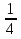 + +
|
Решите уравнение (cos2x-2)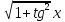 = -1.(Учащиеся группы С решают самостоятельно). Коментируя каждый этап решения этого уравнения. Одновременно постепенно открывается шторка интерактивной доски. = -1.(Учащиеся группы С решают самостоятельно). Коментируя каждый этап решения этого уравнения. Одновременно постепенно открывается шторка интерактивной доски.
Решение:1. Упростим уравнение 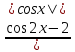 =-1;|cosx| =-1;|cosx|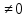
2 x-3=-|cosx| x-3=-|cosx|
2)|cosx|=t, 0 t t 1 1
2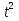 +t-3=0; t=1; t=-3(не удовлетворяет условию 0 +t-3=0; t=1; t=-3(не удовлетворяет условию 0 t t 1) 1)
|cosx|=1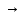 x= x=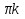 ,k ,k
Ответ. x=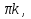 k k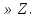
Учащиеся группы А решают самостоятельно тест с последующей проверкой с помощью кликкеров:
1)cosx= 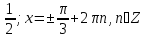 (3) (3)
2)cosx=1; x = 2 (3) (3)
3)cosx= -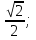 x = x =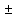 ( (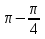 )+2 )+2 ; ;
x= + 2 + 2 (1) (1)
4)sinx =  ,x= ,x=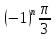 + + (3) (3)
5)tgx = -1,x= -arctg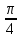 + +  n,n n,n Z (2) Z (2)
Ключ для проверки тестов:33132
Учащиеся группы В работают с с рабочими листами, последовательно отвечая на вопросы в этих листах и самостоятельно добиваясь решения
более сложного тригонометрического уравнения.
I вариант
|
II вариант
|
5 x+ 6sinx -6=0 x+ 6sinx -6=0
5(1-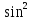 x) +6sinx-6=0 x) +6sinx-6=0
5-5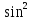 x +6sinx-6=0 x +6sinx-6=0
-5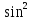 x +6 x +6 - 1=0 - 1=0
5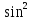 x – 6sinx +1=0 x – 6sinx +1=0
sinx = t, |t| 1 1
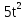 -6t + 1=0 -6t + 1=0
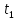 = 1; = 1;  = =
sinx = 1, x=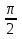 +2 +2
sinx =  , x= , x= arcsin arcsin + +
|
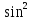 x +2sinxcosx - 3 x +2sinxcosx - 3 x = 0 x = 0
 x + 2tgx – 3=0 x + 2tgx – 3=0
tgx =t,t-любе действительное число
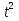 +2t-3=0 +2t-3=0
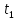 =1, =1, =-3 =-3
tgx=1,x=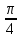 + +
tgx= - 3,x= + +
|
Ответ.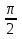 +2 +2 arcsin arcsin + +
|
Ответ. x=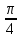 + + + +
|
У каждого ученика из группы А лежат карточки с тригонометрическими уравнениями, выберите те, которые имеют решение и прикрепите при помощи магнитов с одной стороны доски, а те которые не имеют решение с другой. Группы В и С корректируют и объясняют.
(Слайд №14) Итак сегодня мы рассмотрели решение уравнений cost =a, sint=a, tgt =a, а уравнение ctgt = a сводится к уравнению tgt=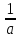 ,a ,a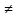 0 0
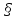 20 п.1,2,3, №349-352(а) для группы А 20 п.1,2,3, №349-352(а) для группы А
+№357(б),№363(б) для группы В
+уравнение из рабочего листа для группыС
| |
|
|
 Скачать 74.15 Kb.
Скачать 74.15 Kb.




 ;tg140;ctg290;sin
;tg140;ctg290;sin .
.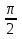 – t);cos(2
– t);cos(2 + t); tg(
+ t); tg( -t); ctg(180- t); sin(270-t)
-t); ctg(180- t); sin(270-t) ) = -
) = - 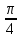 ; arcsin
; arcsin =
=  ; arcsin(-
; arcsin(- 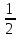 ) =
) =  ; arctg
; arctg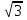 = не существует; arctg(- 1) =
= не существует; arctg(- 1) = 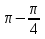
 .
.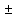
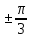 +
+  2x- sin²2x=
2x- sin²2x=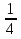
 arccos
arccos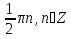
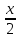 =0,
=0,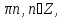
 n
n Z.
Z.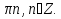
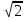
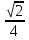
 (
(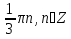

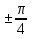 +
+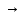 tgx =
tgx = 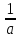 ,a
,a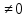
 +
+ +
+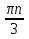 ,n
,n .
. +
+
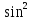 x-5|sinx|+1=0
x-5|sinx|+1=0
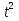 -5t+1=0
-5t+1=0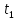 =1,
=1, =
=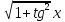 = -1.(Учащиеся группы С решают самостоятельно). Коментируя каждый этап решения этого уравнения. Одновременно постепенно открывается шторка интерактивной доски.
= -1.(Учащиеся группы С решают самостоятельно). Коментируя каждый этап решения этого уравнения. Одновременно постепенно открывается шторка интерактивной доски.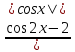 =-1;|cosx|
=-1;|cosx| x-3=-|cosx|
x-3=-|cosx| t
t 1
1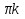 ,k
,k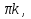 k
k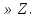
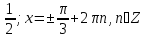 (3)
(3)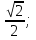 x =
x = + 2
+ 2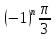 +
+ Z (2)
Z (2) - 1=0
- 1=0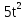 -6t + 1=0
-6t + 1=0
 arcsin
arcsin x + 2tgx – 3=0
x + 2tgx – 3=0 +
+ arcsin
arcsin +
+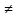 0
0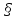 20 п.1,2,3, №349-352(а) для группы А
20 п.1,2,3, №349-352(а) для группы А