Решение показательных и логарифмических уравнений в классах с углубленным изучением математики. Учитель математики Куликова Н. В
 Скачать 45.29 Kb. Скачать 45.29 Kb.
|
| МОУ «Средняя общеобразовательная школа №22 с УИОП» Решение показательных и логарифмических уравнений в классах с углубленным изучением математики. Учитель математики Куликова Н.В. Решению показательных и логарифмических уравнений в школьном курсе алгебры и начал математического анализа уделяется большое внимание, так как изучение этого вопроса открывает широкие возможности для четкого восприятия свойств функции, а также для повторения некоторых ранее изученных разделов алгебры (решение квадратных уравнений и т.д.) Показательные уравнения принадлежат к классу уравнений, носящих название трансцендентных уравнений. Для этих уравнений нельзя указать общего способа решения. До окончательного решения трансцендентного уравнения неясно, сколько оно имеет корней. При решении показательных уравнений возможно получение посторонних корней, поэтому в тех случаях, где это необходимо, корни следует проверять подстановкой. Показательные уравнения можно разбить на три типа, каждый из которых решается определённым способом. К перовому типу можно отнести уравнения, в которых равные основания даны в неявном виде. Например: 1) Исходное уравнение свелось к уравнению вида С учетом изложенного уравнение (*) равносильно уравнению 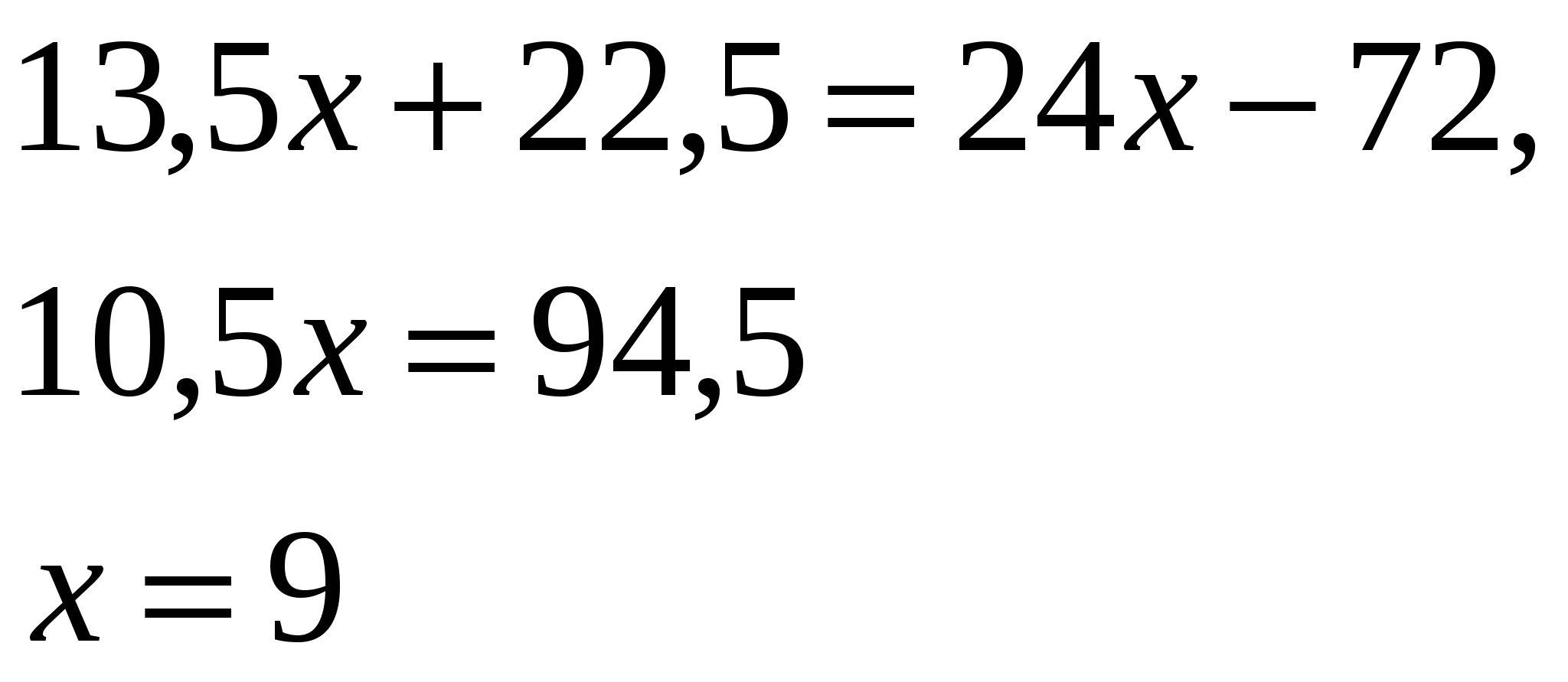 Необходимо сделать проверку, т.к. областью допустимых значений Х является не всё множество действительных чисел. Проверка : 2) Можно разделить левую и правую части уравнения на произведение Исходное уравнение свелось к уравнению Проверка: Ко второму типу можно отнести уравнения, левая часть которых требует предварительного разложения на множители. Например: 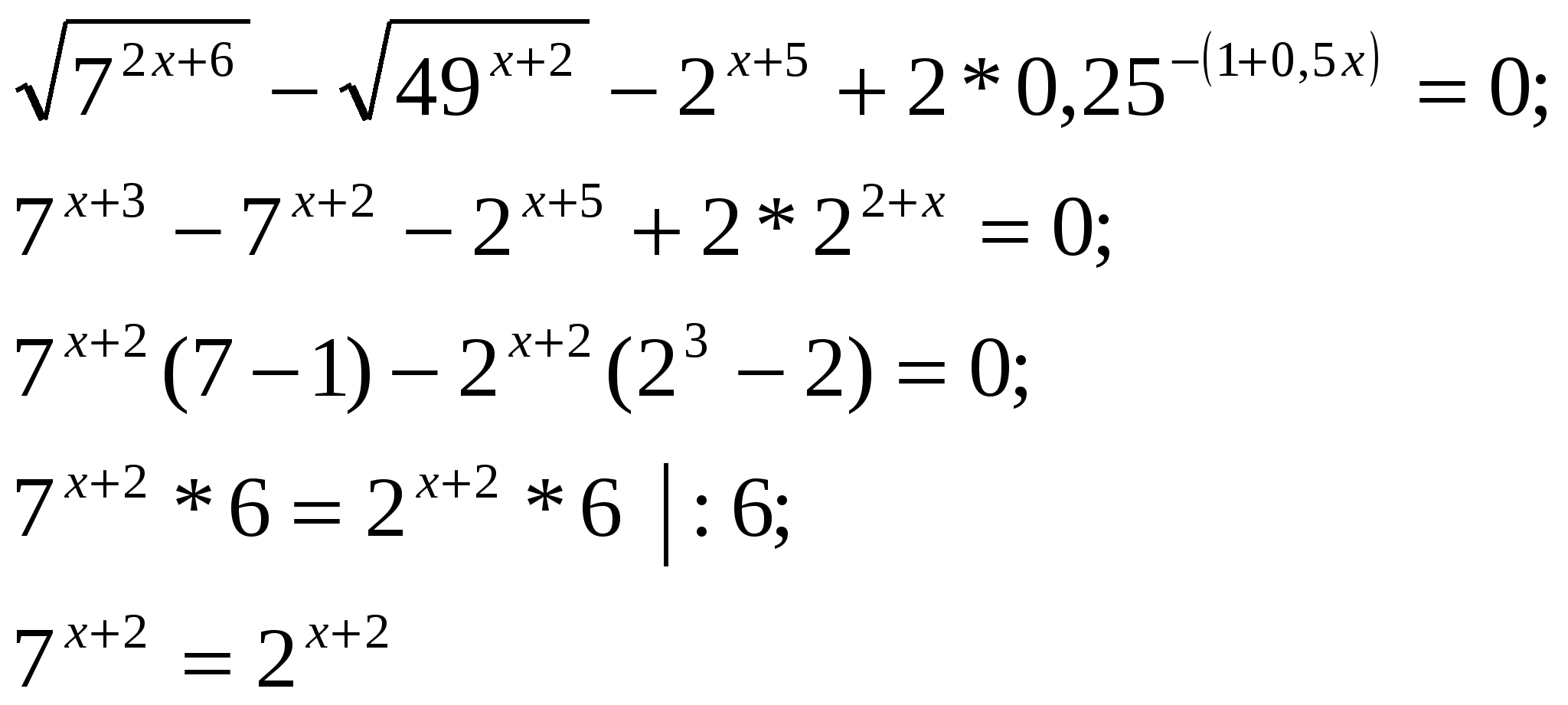 Степени равны, показатели степеней тоже равны при неравных основаниях, значит показатели степеней равны 0, т.е. Проверка: К третьему типу можно отнести уравнения, решение которых сводится к решению квадратного уравнения. При этом используется метод введения новой переменной с отбором корней на промежуточном этапе. Например: Если обозначить 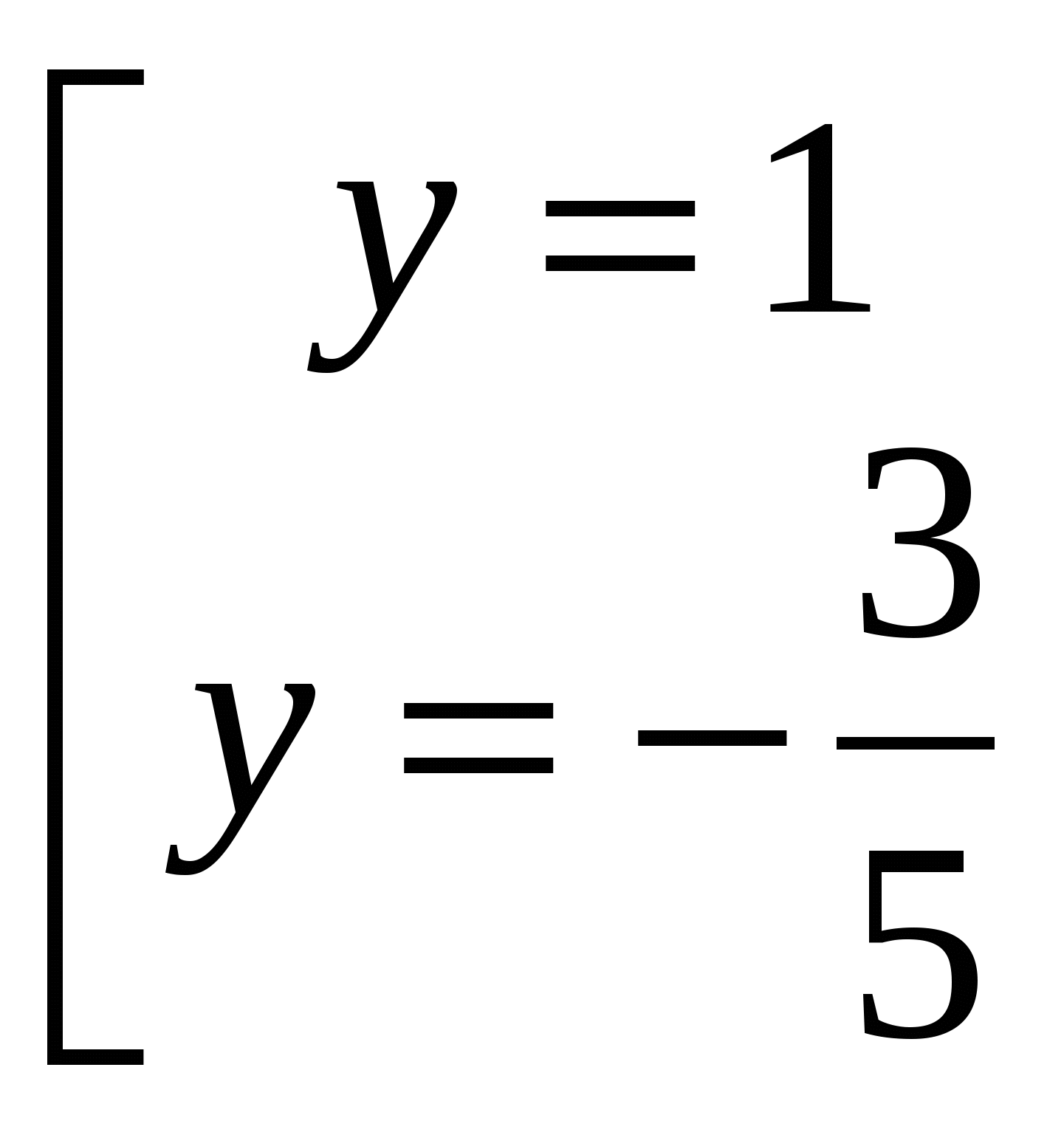 Далее: 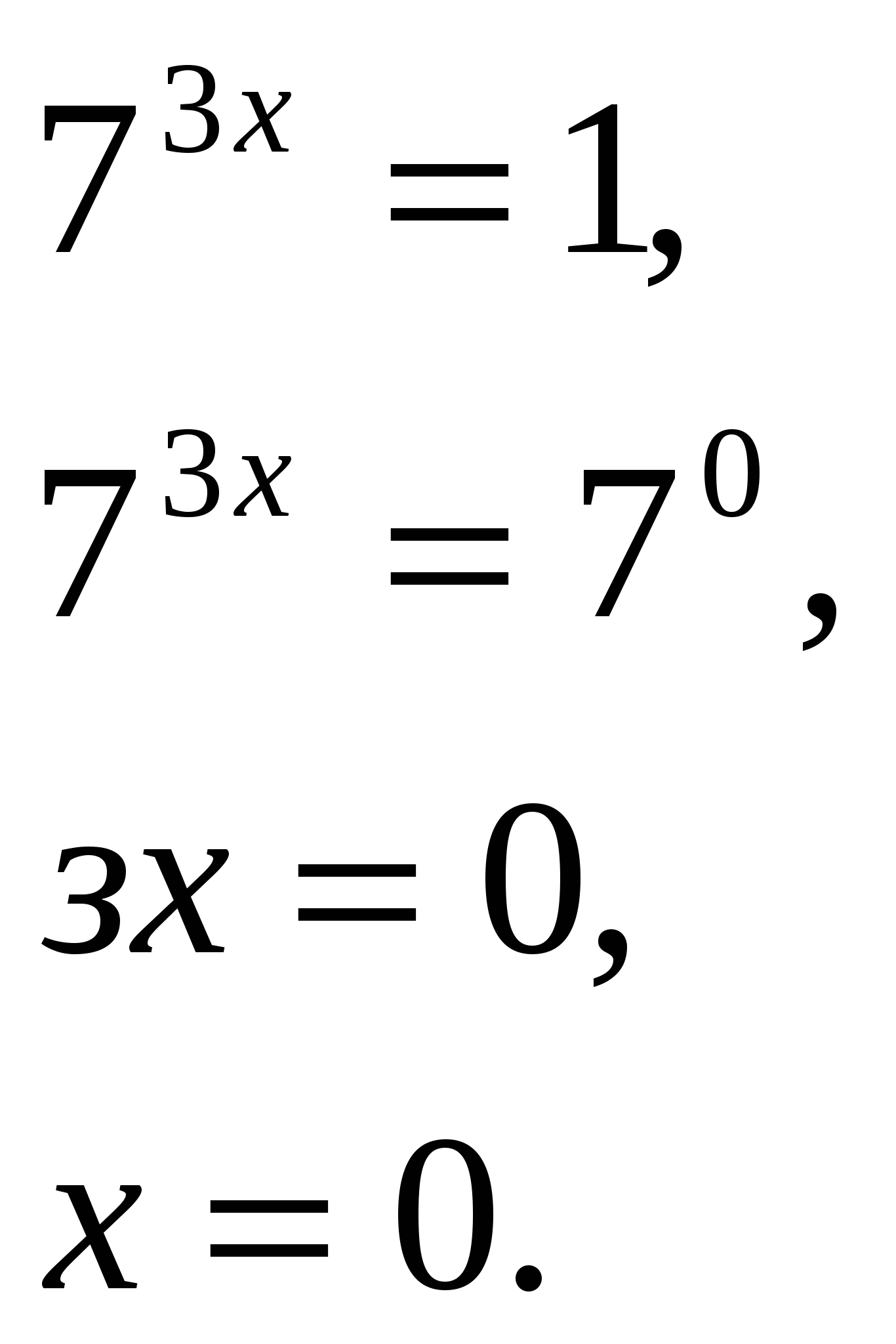 В данном случае необходимости в проверке не существует. Решение простейших логарифмических уравнений связано с определением логарифма и основным логарифмическим тождеством вида На основании определения логарифма решаются задачи, в которых по данным основаниям и числу определяется логарифм, по данному логарифму и основанию определятся число и по данному числу и логарифму определятся основание. Решения уравнений вышеприведенного характера обычно затруднений не вызывают. В школьной программе чаще всего встречаются уравнения, которые решаются либо непосредственным потенцированием, либо потенцированием с предварительным упрощением данного выражения, либо логарифмированием обеих частей уравнения. Например: 1) Желательно, не приступая к решению уравнения, найти область допустимых значений функции, стоящей в левой части уравнения. При наличии предварительного исследования проверку делать не обязательно. Если же исследование не проводится, то проверка решения необходима. В данном случае Далее С учётом проведенного исследования проверка решения не нужна. 2) 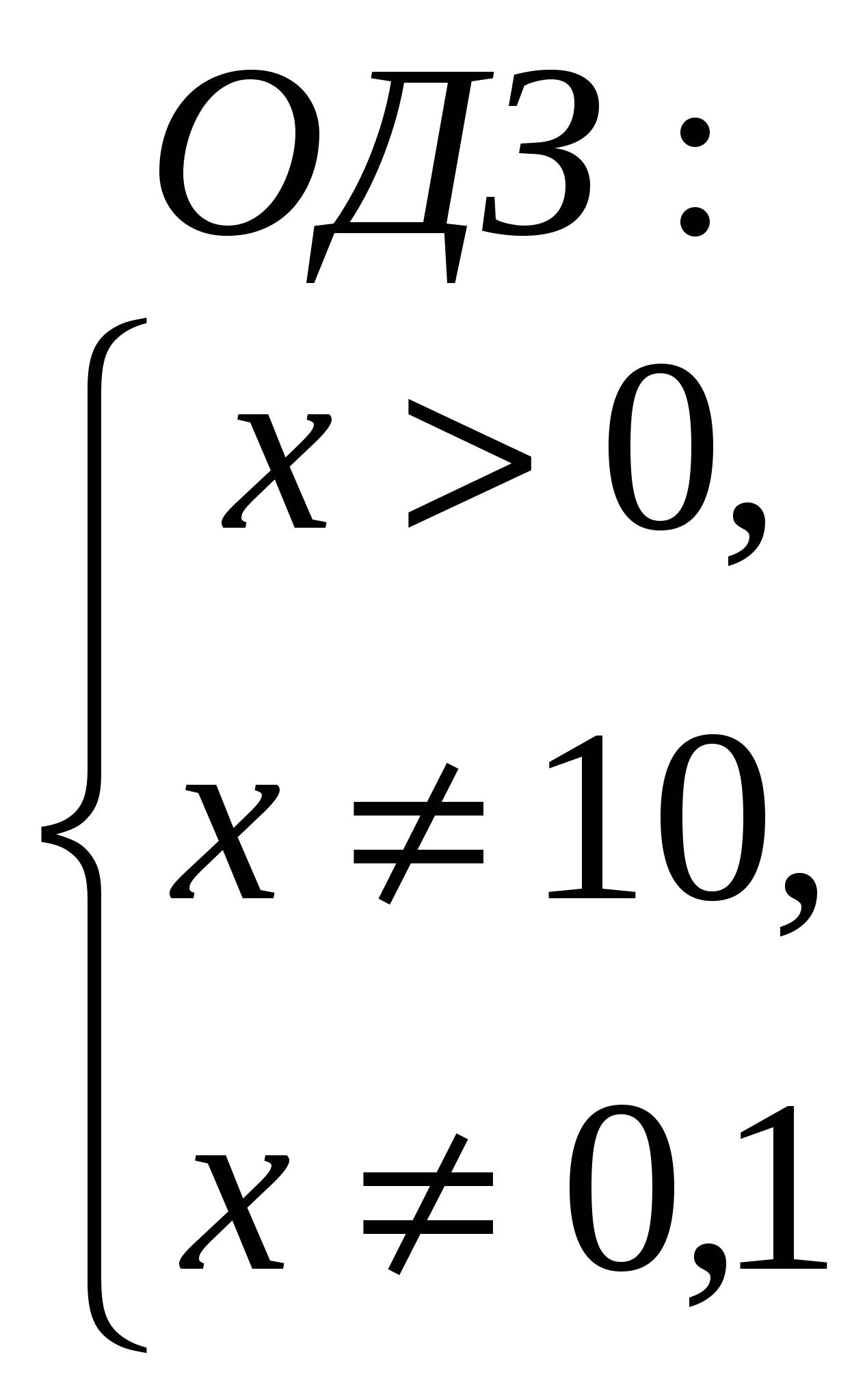 С учётом проведенных исследований возможно перейти к решению уравнения 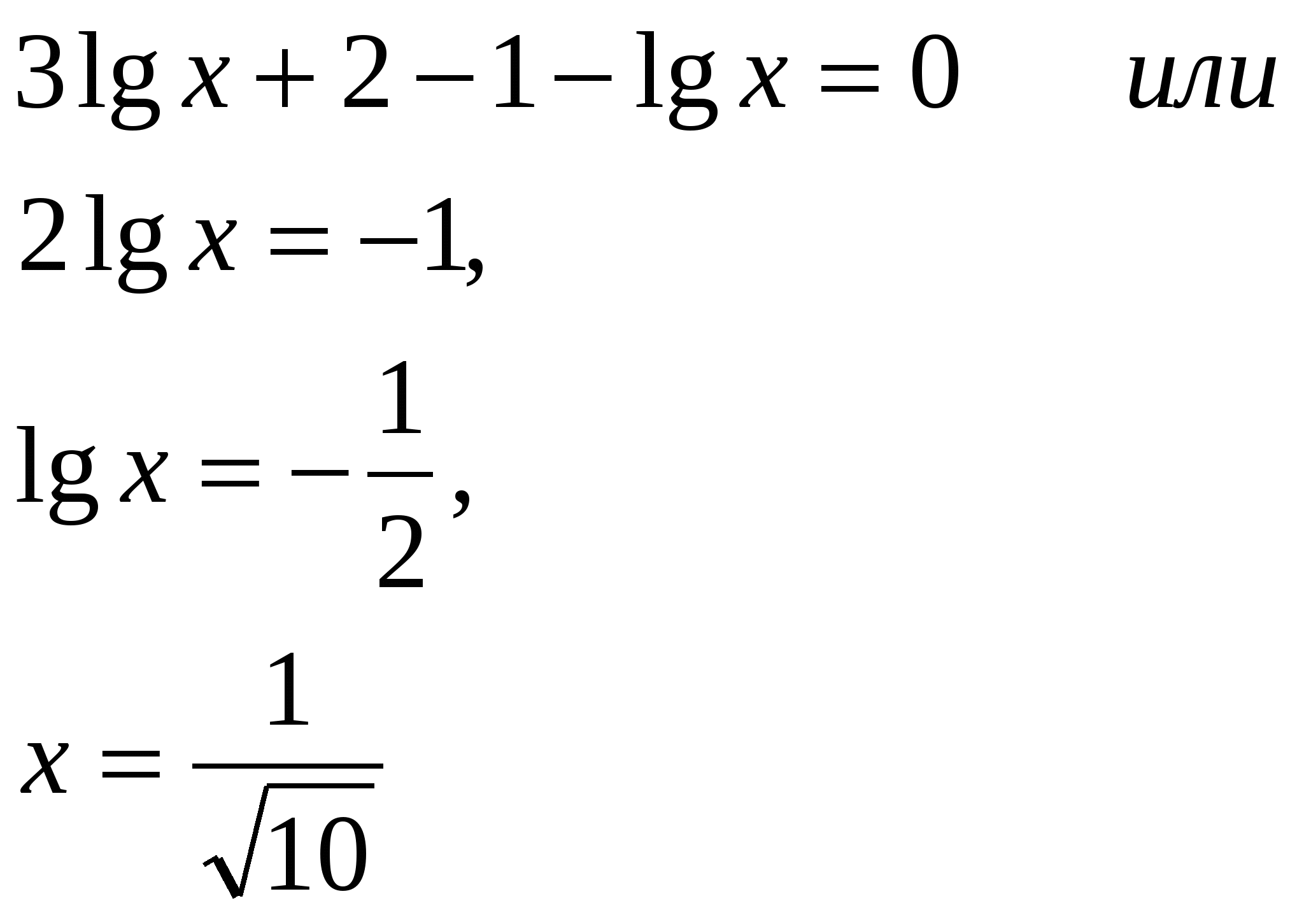 Данное решение удовлетворяет ОДЗ, следовательно 3) Необходимо прологарифмировать обе части уравнения по основанию 10 Далее Решив данное уравнение относительно С учётом ОДЗ Логарифмирование обеих частей уравнения используется в основном для уравнений, в которых показатель степени содержит логарифмы. Несколько примеров решения уравнений с усложнёнными условиями: 1) Естественно заметить, что 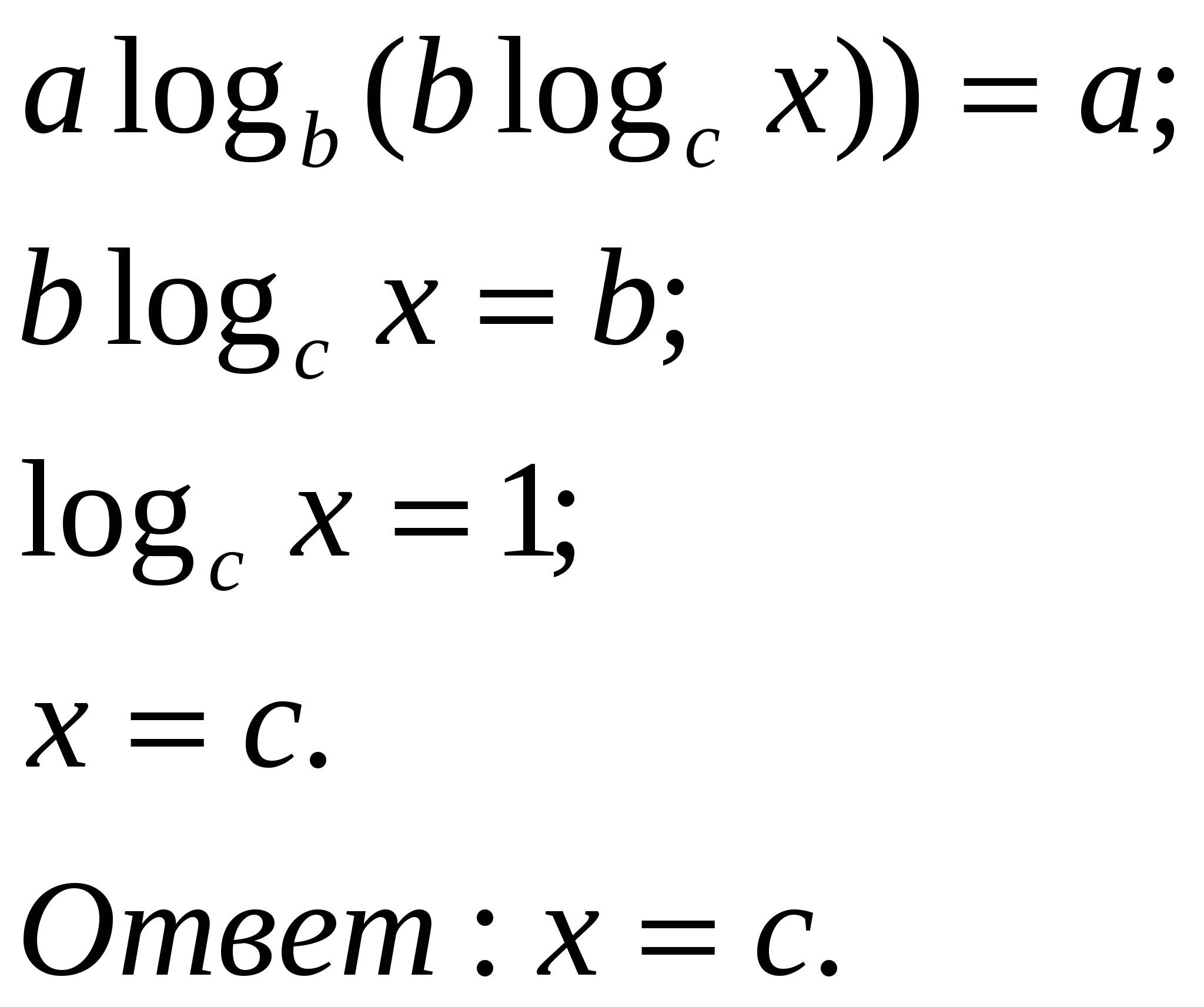 2) 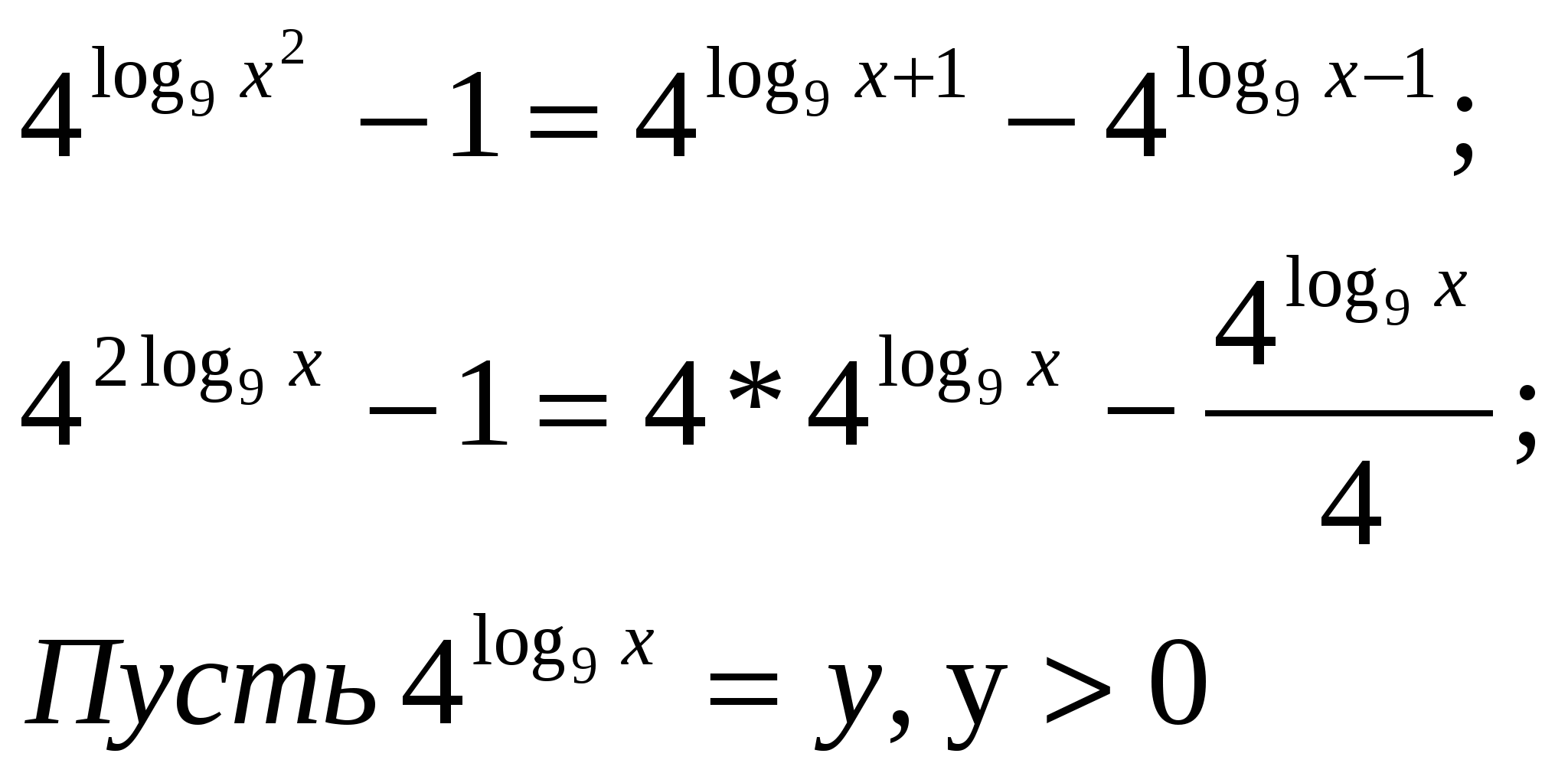 Тогда с учетом новой переменной исходное уравнение примет вид 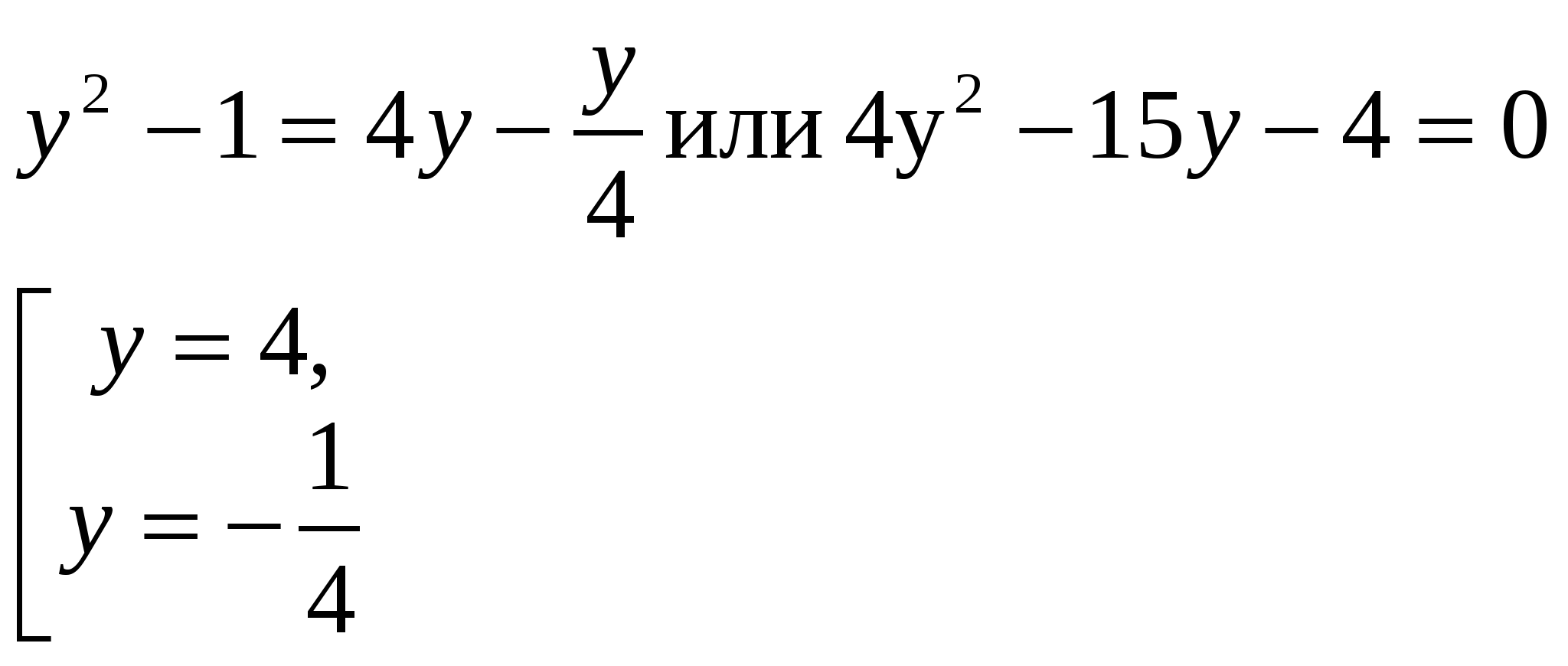 Далее 3) 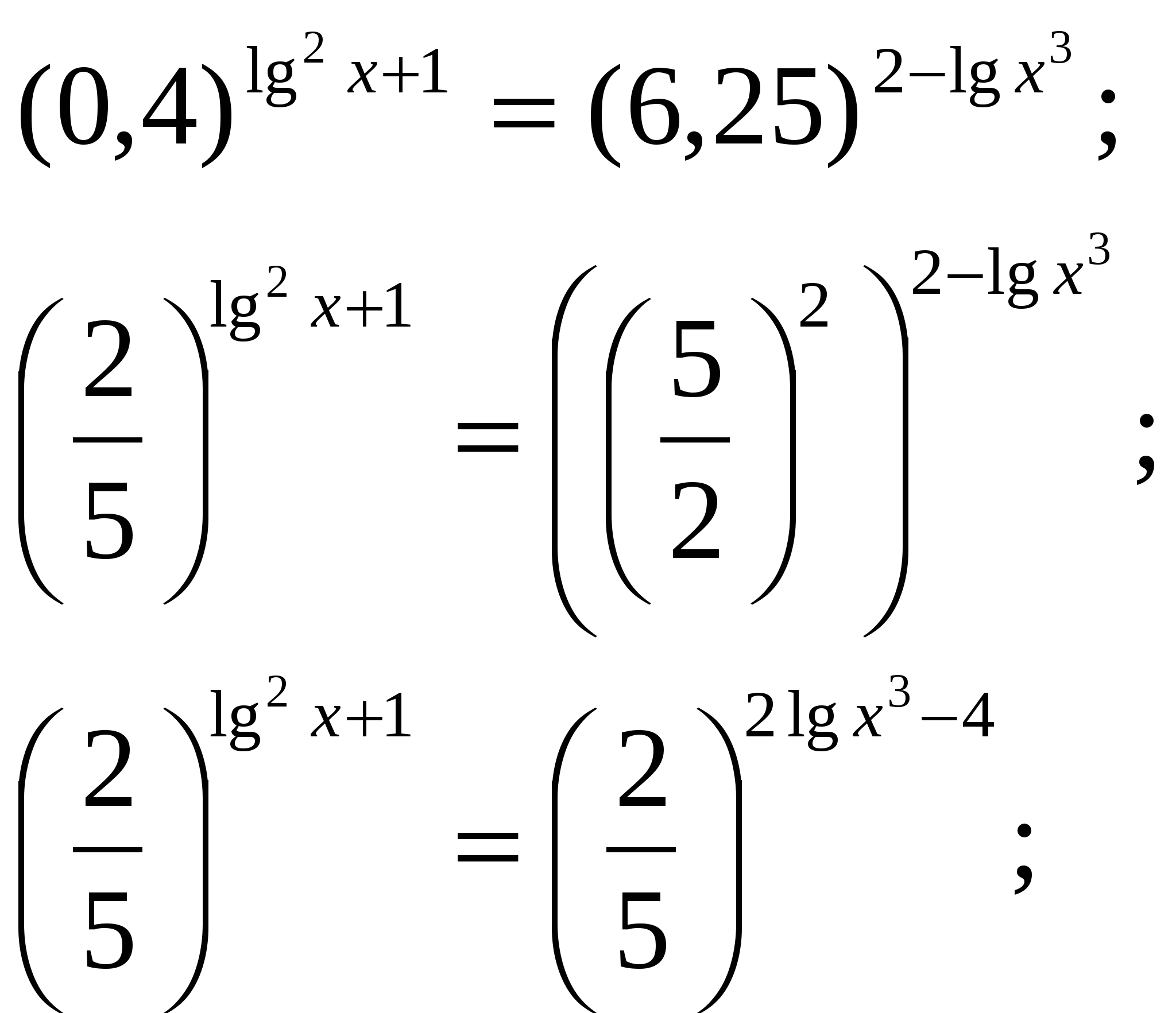 Решив данное уравнение относительно 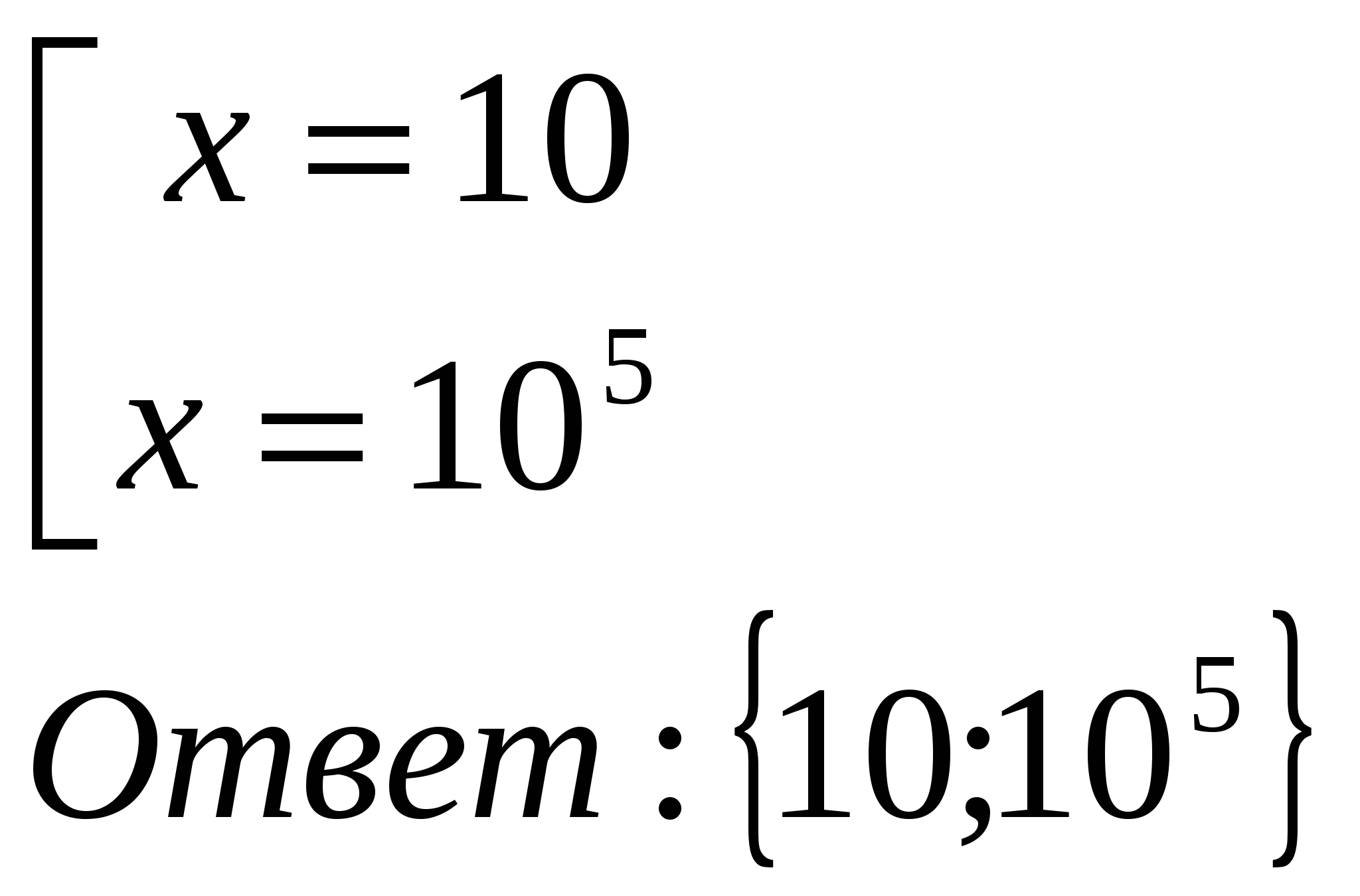 |