«Тригонометрические уравнения с условием ( отбор корней )»
 Скачать 26.81 Kb. Скачать 26.81 Kb.
|
| Открытый урок по алгебре и началам анализа в 10а классе 7. 11.11 ( фрагменты поурочного плана ) Тема: « Тригонометрические уравнения с условием ( отбор корней )» Цели: Первый уровень – сегодня. Ключевое слово ПОНЯТЬ. Понять все три способа отбора корней простейших тригонометрических уравнений (т. у. ) Второй уровень – на следующей паре. Ключевое слово НАУЧИТЬСЯ. Научиться проводить отбор корней простейших т. У. Третий уровень – в конце изучения тригонометрии. Научиться проводить отбор корней любого т.у. Ход урока.
Первый вывод: отбор корней провели с помощью числовой окружности.
Работа с учебником. Первая часть стр. 187 пример №11. Комментарий учителя. Второй вывод: отбор корней провели методом перебора значений параметра п. Рассмотрели примеры, где задания по отбору корней даны в явном виде. Часто пор отбор корней в заданиях вообще ничего не говорится, но в ходе решения он присутствует. Последние три года на ЕГЭ в задании С1 приводятся примеры по отбору корней.
Получили уравнение с условием. Мы рассмотрели два способа отбора корней есть и другие способы отбора.
Первый способ. Отбор корней проведем с помощью числовой окружности. На числовой окружности отложатся точки, соответствующие числам 3Х, а по условию надо найти Х. Обозначим границы 3Х. Таковыми являются 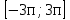 . Корни уравнения симметричны относительно начала координат, поэтому достаточно найти положительные корни и в ответ добавить им противоположные. На промежутке от 0 до 2п корнями являются числа: . Корни уравнения симметричны относительно начала координат, поэтому достаточно найти положительные корни и в ответ добавить им противоположные. На промежутке от 0 до 2п корнями являются числа: 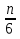 и и 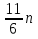 . На промежутке от 2п до 3п корнем будет число . На промежутке от 2п до 3п корнем будет число 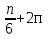 . Далее получаем: 3Х1 = . Далее получаем: 3Х1 = 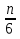 , Х1 = , Х1 = 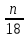 , 3Х2 = , 3Х2 = 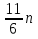 , Х2 = , Х2 = 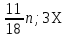 3 = 3 = 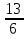 п, Х3 = п, Х3 = 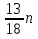 . Ответ: ± . Ответ: ± 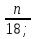 ; ; 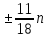 ; ± ; ± 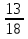 п. п.Второй способ. Отбор корней проведем с помощью двойного неравенства. Одной из серий решения неравенства является выражение Х = 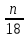 + + 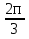 п. Необходимо решить двойное неравенство – п ≤ п. Необходимо решить двойное неравенство – п ≤ 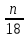 + + 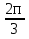 п ≤ п, - п ≤ п, - 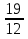 ≤ п ≤ ≤ п ≤ 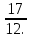 , п – целые числа. П = -1, 0, 1. При п = -1 Х = , п – целые числа. П = -1, 0, 1. При п = -1 Х = 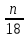 - - 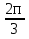 = - = - 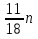 ; при п = 0 Х = ; при п = 0 Х = 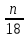 ; при п = 1 Х = ; при п = 1 Х = 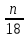 + + 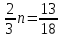 п. Учитывая, что корни симметричны относительно начала координат получаем тот же ответ. п. Учитывая, что корни симметричны относительно начала координат получаем тот же ответ.Третий вывод: отбор корней провели методом решения двойного неравенства.
Учитель В.П.Коневцев |
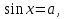
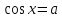 , которые принадлежат отрезкам ( удовлетворяют условию ). Можно использовать числовую окружность.
, которые принадлежат отрезкам ( удовлетворяют условию ). Можно использовать числовую окружность.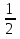
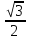
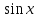
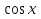
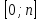
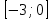
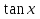 ≤ 0
≤ 0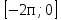
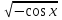 + 1 ) =0 Решить уравнение. Найдите ОДЗ этого уравнения. -
+ 1 ) =0 Решить уравнение. Найдите ОДЗ этого уравнения. - 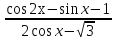 = 0. Решить уравнение. Найдите ОДЗ этого уравнения.
= 0. Решить уравнение. Найдите ОДЗ этого уравнения. 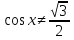
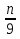 +
+ 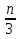 п Читаем далее. « Осталось из найденной
п Читаем далее. « Осталось из найденной 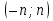 . Решаем двойное неравенство относительно п. Найденные значения п подставляем в формулу корней уравнения. Этот третий способ отбора корней назовем отбор методом двойного неравенства.
. Решаем двойное неравенство относительно п. Найденные значения п подставляем в формулу корней уравнения. Этот третий способ отбора корней назовем отбор методом двойного неравенства.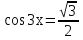 . Найти Х, принадлежащий
. Найти Х, принадлежащий