Решение неравенств второй степени с одной переменной

Скачать 88.69 Kb. Название Решение неравенств второй степени с одной переменной Дата 05.04.2016 Размер 88.69 Kb. Тип Урок

Разработка открытого урока по алгебре в 9 классе. Тема: Решение неравенств второй степени с одной переменной. Тип урока: закрепления знаний и способов учебных действий. Цели урока: 1. Образовательная: формирование навыков решения неравенств второй степени с одной переменной на основе свойств квадратичной функции. 2. Развивающая: развитие навыков самоконтроля, взаимоконтроля, самооценки. 3. Воспитательная: воспитание взаимопонимания, взаимоуважения, чувства ответственности. Технологии: дифференцированное обучение, технология обучения в сотрудничестве. Оборудование и материалы: компьютер, проектор, тесты, листы оценивания, презентация «Решение неравенств второй степени с одной переменной», карточки, магниты. Ход урока. 1 этап. Организационный момент. Здравствуйте, ребята и гости! Я рада сегодняшней встрече с Вами, посвященной Юбилею нашей родной школы. 2 этап. Актуализация знаний. Фронтальный опрос. Урок мне хочется начать со слов персидского поэта Рудаки: «С тех пор как существует мирозданье, Такого нет, кто б не нуждался в знанье». Ребята, как вы понимаете эти строки? (Дети высказываются). Мы с вами тоже сегодня будем закреплять свои знания. Ребята, какую тему мы сейчас изучаем? (Решение неравенств второй степени с одной переменной). Слайд 1. Тема: Решение неравенств второй степени с одной переменной. Цель: совершенствование навыков решения неравенств второй степени с одной переменной. (Один ученик читает цель урока со слайда). Дайте определение неравенства второй степени с одной переменной. (Неравенства вида ах2 + вх + с > 0 и ах2 + вх + с < 0, где х – переменная, а, в, с – некоторые числа, причем а ≠ 0, называют неравенствами второй степени с одной переменной). Слайд 2. ах2 + вх + с > 0 ах2 + вх + с < 0 х – переменная а, в, с – некоторые числа, а ≠ 0 Выберите из данных неравенств неравенства второй степени с одной переменной. Слайд 3. 1) х2 + 2х – 48 < 0 6) (х – 1)(х – 2) ≥ 0 2) х2 – 6 ≤ 0 7) 3х - 17 х2 > 0 3) 7х + 2 х2 > 4 8) 5х2 –у > 9 4) х – 3 > 0 9) - 3 х2 -6х + 9 < 0 5) – 20 х2 ≤ 5 3 Почему не назвали 4 и 8 ? (4 – линейное неравенство, 8 – с двумя переменными). Что называется решением неравенства с одной переменной? (Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство). Что может быть решением неравенства второй степени с одной переменной? (Промежуток, число, пустое множество). Слайд 4. Решение неравенства Промежуток Пустое множество Число Что значит - решить неравенство? (Решить неравенство – значит найти все его решения или доказать, что их нет). Какие неравенства называются равносильными? (Неравенства, имеющие одни и те же решения, называются равносильными. Неравенства, не имеющие решений, также считаются равносильными). Вспомним алгоритм решения неравенств второй степени с одной переменной. (Учащиеся говорят, на слайде появляются шаги алгоритма). Слайд 5. Алгоритм решения неравенств второй степени с одной переменной. 1. Привести неравенство к виду ах2 + вх + с > 0 (ах2 + вх + с < 0). 2. Ввести функцию f (х) = ах2 + вх + с и охарактеризовать её. 3. Найти нули функции, т.е. решить уравнение f (х) = 0. 4. Отметить на оси х нули функции и изобразить схематически параболу. 5. Отметить промежутки, которые будут являться решениями данного неравенства (внимательно смотреть знак неравенства). 6. Записать ответ. Какие знания нам здесь нужны? (Перечисляем: 1)Тождественные преобразования. 2) Свойства квадратичной функции: зависимость направления ветвей параболы от коэффициента а, свойство знакопостоянства. 3) Нахождение корней квадратного трехчлена. 4) Изображение параболы. 5) Запись числового промежутка. Молодцы! 3 этап. Проверка домашнего задания. А теперь проверим домашнее задание. Поменяйтесь, пожалуйста, тетрадями. Ответы на слайде. (Взаимопроверка в парах) Слайд 6. 1) (- 5; 5) 2) (- ∞; -] U [ ; + ∞) 3) [ -1,5; 5] 4) (- ∞; 6) U (12; + ∞) 5) (-∞; + ∞) Критерии оценки: «3» - 3 верных задания «4» - 4 верных задания «5» - 5 верных заданий Поставьте оценки в листы оценивания. Лист оценивания. Фамилия, имя __________________ Вид работы Домашняя работа Работа в паре Тест Оценка 4 этап. Решение тренировочных упражнений. 1)Работа в группах. На доске зашифрована фраза. Чтобы её отгадать, необходимо выполнить задания на листах № 1: решить данные неравенства, соотнести решения неравенств с ответами на карточках, лишнюю карточку с расшифрованным словом прикрепить магнитами на доску. Лист № 1. Решите данные неравенства, соотнесите решения неравенств с ответами на карточках, лишнюю карточку с расшифрованным словом прикрепите магнитами на доску. 1. Решите неравенство: х2 – 16 ≥ 0 2. Найдите множество решений неравенства: 2 х2 – 7х + 6 > 0 3. Найдите область определения функции: 4. Решите неравенство: 2 (-х2 + 5х) ≥ 18 – 2х (Учащиеся составляют фразу «Нашей школе 45 лет!») Молодцы! Справились с заданием! 2) Работа в парах. А сейчас, ребята, вы побываете в роли учителя. Проверьте работу ученика 9кл., находящуюся на листе № 2. Ошибки подчеркните. Слайд 7. Лист № 2. № 1. Решите неравенство: х2 – 5х + 6 < 0 f(х) = х2 – 5х + 6 – квадратичная функция, график – парабола, 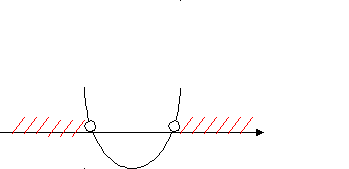ветви вверх. х2 – 5х + 6 = 0 х1 = 2 х2 = 3 2 3 x Ответ: ( 2; 3 ) № 2. Найдите множество решений неравенства: - 0,2 х2 + х – 1,2 ≤ 0 f(х) = - 0,2 х2 + х – 1,2 - квадратичная функция, график – парабола, ветви вниз. - 0,2 х2 + х – 1,2 = 0 / * ( - 5) 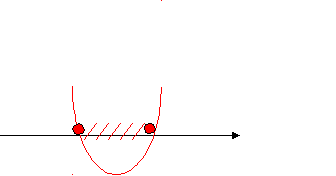х2 – 5х + 6 = 0 х1 = 2 х2 = 3 2 3 x Ответ: ( -∞; 2 ) U ( 3; + ∞) № 3. Решите неравенство: 2х > х2 2х - х2 > 0 f(х) = 2х - х2 - квадратичная функция, график – парабола, ветви вниз. 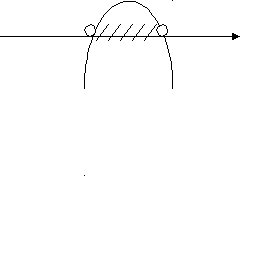2х - х2 = 0 х ( 2 – х ) = 0 х = 0 или х = 2 0 2 x Ответ: [ 0; 2 ] № 4. Найдите множество решений неравенства: 1 + 2х + х2 > 0 f(х) = 1 + 2х + х2 - квадратичная функция, график – парабола, 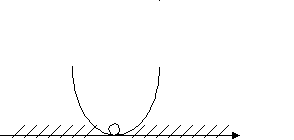ветви вниз. 1 + 2х + х2 = 0 х2 + 2х +1 = 0 х = - 1 -1 x Ответ: - 1 Внимание на слайд! Посчитайте количество верно найденных ошибок. На слайде они выделены красным цветом. Слайд 8. Критерии оценки: «3» - 3-4 найденных ошибки «4» - 5-6 найденных ошибок «5» - 7 найденных ошибок Поставьте оценку в свой лист оценивания. 3) Решение на доске и записью в тетрадях (1 ученик на доске с объяснением). Ребята, вам всем предстоит в этом году сдавать государственные экзамены. Рассмотрим задание из сборника для подготовки к ГИА. Слайд 9. Найдите все целые решения неравенства, принадлежащие промежутку [ - 2; 2 ] 2 х2 ≤ х + 3 9 3 5 этап. Контроль знаний. Тестирование с последующей взаимопроверкой. Лист № 3. Тест. 1 вариант. 1. На каком рисунке изображено множество решений неравенства х2 – 9 ≤ 0 ? 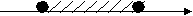а) б) -3 3 x 3 x 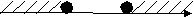в) г) -3 x -3 3 x 2. Решите неравенство: х2 – 8х + 15 > 0 а) ( 3; 5) б) [ 3; 5 ] в) (- ∞; 3) U (5; + ∞) г) (- ∞; 3 ] U [ 5; + ∞) 3. Найдите множество решений неравенства: 5х - х2 ≥ 0 а) [ 0; 5] б) (- ∞; 0) U (5; + ∞) в) (- 5; 0) г) (- ∞; 0 ] U [5; + ∞) 4. Решите неравенство: 6а < а2 + 10 а) ( - 4; + ∞) б) решений нет в) ( - ∞; 4) U (36; + ∞) г) ( - ∞; + ∞ ) 5. Найти область определения функции: у = а) (- ∞; 0) U (4; + ∞) б) (0; 4) в) (- ∞; 8 ] U [2; + ∞) г) [ 0; 4 ] Тест. 2 вариант. 1. На каком рисунке изображено множество решений неравенства х2 – 49 ≥ 0 ? 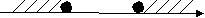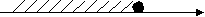а) б) -7 7 x 7 x в) г) -7 7 x -7 x 2. Решите неравенство: х2 – 10х + 21 < 0 а) (- ∞; 3) U (7; + ∞) б) (- ∞; 3 ] U [7; + ∞) в) [ 3; 7 ] г) ( 3; 7) 3. Найдите множество решений неравенства: 2х - х2 ≤ 0 а) (- ∞; 0 ] U [2; + ∞) б) [0; 2] в) (0; 2) г) (- ∞; 0 ] U [2; + ∞) 4. Решите неравенство: 8в – 17 < в2 а) ( - 4; + ∞) б) ( - ∞; + ∞ ) в) ( - ∞; 4) U (64; + ∞) г) решений нет 5. Найти область определения функции: у = а) (- ∞; - 3] U [6; + ∞) б)(- ∞; 0) U (2; + ∞) в) (0; 2) г) [ 0; 2 ] Слайд 10. Проверяем соседа. 1 вариант. 2 вариант. а а в г а а г б б в Критерии оценки: «3» - 3 верных задания «4» - 4 верных задания «5» - 5 верных заданий Поставьте оценки в листы оценивания. 6 этап. Обобщение (устно) Итак, сегодня мы решили много различных заданий. Решение каждой задачи сводилось к решению неравенства второй степени с одной переменной на основе свойств квадратичной функции. Ребята, у меня к вам вопрос. Слайд 11. х2 – 12х + 35 Какие задачи можно составить с квадратным трехчленом х2 – 12х + 35, чтобы при их решении возникла необходимость решить неравенство второй степени с одной переменной ? ( 1. Решите неравенство … 2. Найдите множество решений неравенства … 3. Найдите область определения функции … 4. При каких значениях х квадратный трехчлен принимает положительные (отрицательные) значения). 7 этап. Домашнее задание. Выберите, пожалуйста, домашнее задание и запишите в дневник. Слайд 12. Домашнее задание. 1 уровень - № 116 (г, д, е) 2 уровень - № 124 3 уровень - № 3.10(2), 3.11 (из сборника для подготовки к ГИА). 8 этап. Рефлексия. Ребята, какая цель стояла сегодня перед вами? Слайд 13. Цель: совершенствование навыков решения неравенств второй степени с одной переменной. Как вы считаете, достигнута ли она? (дети высказываются) Ребята, возьмите со стола звезду. В центре напишите своё имя. В верхнем луче напишите виды деятельности, которыми вы занимались на уроке. В правом луче перечислите тех, кто помогал вам сегодня на уроке. В левом луче – термины, прозвучавшие на этом уроке. В правом нижнем луче – довольны ли вы своей работой на уроке. В левом нижнем луче – каким стало ваше настроение. Молодцы! Сегодня все работали очень хорошо! Ребята, каждый из вас индивидуален и неповторим. Вы талантливы! Вы звезды! Поднимите звезды вверх, порадуйтесь за себя и своих друзей. Замечательно! Я всех благодарю за работу. Желаю, чтобы наша школа славилась такими успешными учениками, как вы! До новых встреч! Используемая литература. 1. Алгебра 9 класс. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, Москва, «Просвещение», 2009 г. 2. Дидактические материалы. Алгебра 9 класс, Ю.Н. Макарычев, Н.Г. Миндюк, Л.М. Короткова, Москва, «Просвещение», 2012 г. 3. Алгебра. Сборник заданий для подготовки к итоговой аттестации в 9 классе. Л.В. Кузнецова, С.Б. Суворова, Е.А. Бунимович, Москва, «Просвещение», 2009 г. 4. Журнал «Математика в школе», № 2, 1998 г.