|
Квадратние неравенства
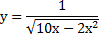 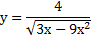 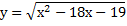 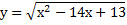  ПЛАН УРОКА-ПРЕЗЕНТАЦИИ ПЛАН УРОКА-ПРЕЗЕНТАЦИИ
Подготовила: Агабабян Мариам Микаеловна, учитель математики
Класс: 9.
Предмет: Алгебра
Тема: Квадратние неравенства
Урок №
|
Тема урока
|
Аннотация
|
1
|
Знак квадратного трехчлена
|
Знать построение графиков квадратичной функции. Уметь определить расположение ветвей, знать нули функции, наибольшее /наименьшее/ значение функции.
|
2
|
Решение квадратных неравенств
|
Иметь представление о квадратном неравенстве , об их прикладном значении, об области допустимых значений, уметь решать квадратные неравенства с помощью графиков квадратной функции, уточнять данное число является корнем неравенства
|
3
|
Решение квадратных неравенств
|
Иметь представление о квадратном неравенстве , об их прикладном значении, об области допустимых значений, уметь решать квадратные неравенства с помощью графиков квадратной функции, уточнять данное число является корнем неравенства
|
4
|
Решение нестрогих неравенств второй степени.
|
Уметь решать нестрогие неравенства, с учетом того, что знают решение строгих неравенств второй степени с помощью графика квадратичной функции
|
5
|
Решение нестрогих неравенств второй степени.
|
Уметь решать нестрогие неравенства, с учетом того, что знают решение строгих неравенств второй степени с помощью графика квадратичной функции
|
6
|
Тематическая письменная работа
|
Проверка усвоения материала
|
1-ый вариант
1.Дан квадратный трехчлен: x2+6x-40
2.Решить неравенства:
3. При каких значениях а решениями неравенства -x2+2x+a≤0 являются все действительные числа.
4.Сумма двух чисел равна 13, а их произведение равно 36.Найти эти числа.
2-ой вариант
1.Дан квадратный трехчлен: x2+4x-60
Найти дискриминант
Сколько корней имеет этот трехчлен
Найти корни квадратного трехчлена
Схематически построить график этой функции
2.Решить неравенства:
3. При каких значениях а решениями неравенства x2-8x-a≥0 являются все действительные числа.
4.Сумма двух чисел равна 19, а их произведение равно 90.Найти эти числа.
План урока 1
Тема урока
|
Решение неравенств второй степени
|
Цель урока
|
Ввести понятие неравенства второй степени с одной переменной.
.Формировать знания по решению неравенств аx2+bx+c>(<)0 (a≠0) на основе свойств квадратичной функции.
|
Задачи урока
|
Уметь строить график кв. Функции в зависимости от знаков старшего коэффициента и дискриминанта
Уметь определять промежутки положительного и отрицательного знаков функции.
На основе графика уметь четко записывать решение неравенства второй степени и дать верный ответ.
|
После урока ученики будут знать
|
Расположение графика кв. Функции в координатной плоскости, положительные, отрицательные знаки кв. Функции и его нули.
|
После урока ученики будут уметь
|
Решать кв. неравенства графическим методом.
|
Ход урока
|
1 этап Организационный момент. Учет посещаемости и проверка домашнего задания.
2 этап Устная работа / разбить класс на группы по 4 человека/
Используя график кв. Функции У=ax2+bx+c: / сл. 1/ ответить на вопросы
Охарактеризовать знак старшего члена и дискриминанта
Назвать значения переменной Х , при которых функция принимает значения, равные 0 , положительные и отрицательные значения.
Учитывая свойства кв. Функции указать пересекает ли ось ОХ графики следующих функций:
а/ У=Х2-16 г/У=/Х+3/2
б/У=/Х-5/2 д/ У=/Х-2/2+4
в/ У=Х2+7 е/ У= /Х+4/2-3
Работа ведется по группам по карточкам.
Если да, то в каких точках.
3 этап Изучение нового материала
Фронтальная работа со всем классом.
Коллективная выработка алгоритма решение неравенства второй степени с одной переменной графическим способом / сл.2/
4 этап Первичное закрепление материала.
Учитель решает кв. Неравенства и указывает при решении на все пункты алгоритма /сл.3/
5 этап Тренировочные упражнения.
Решить , по группам N118 и всем классом N112 с комментариями и самопроверкой.
6 этап Подведение итогов.
Повторить алгоритм решения кв. неравенств
Оценить работу в группах
7 этап Дать домашнее задние с пояснением N119,128.
|
План урока 2
Тема урока
|
Итоговый урок по решению кв. неравенств и подготовка к письменной работе
|
Цель урока
|
Повторить свойства кв. Функции, ее график, алгоритм решения нестрогих неравенств второй степени.
|
Задачи урока
|
Актуализировать имеющиеся у учащихся знаний о решение неравенств второй степени графическим способом, провести диагностику и коррекцию ошибок.
|
После урока ученики будут знать
|
Расположение графика кв. Функции в координатной плоскости, положительнее, отрицательные знаки кв. Функции и его нули.
|
После урока ученики будут уметь
|
Решать кв. неравенства графическим методом
|
Ход урока
|
1 этап Организационный момент. Учет посещаемости и проверка домашнего задания.
2 этап Устная работа / разбить класс на группы по 6 человека/
На доске изображены графики функции У=ax2+bx+c
Каждое группа , изучая данный им график, отвечает на вопросы:
Определить знак коэффициентов а, в, с , и дискриминанта
Назвать значения переменной Х , при которых функция равна 0 , больше 0-я, меньше 0-я, принимает наибольшее значение , наименьшее значение возрастает и убывает.
Какие из чисел -2; 0; 3; являются решениями неравенств
а/ Х2-7х+1≥0 б/Х2-Х>0 в/5Х2+2Х-1<0 г/ Х2-2≤0
При решении неравенства ученик получил ответы :
а/ Х≤±7 б/-7<Х<7 в/ Х≥±2 г/Х≥2 и Х≤-3
Могли ли получиться такие ответы?
Если да , то придумайте неравенства имеющие такие решения.
Если нет, объясните, почему вы так считаете .
3 этап Тренировочные упражнения по группам, по 6 человек .
Решить N120, с последующей проверкой и N114 с комментариями.
Выявить ошибки и корректировать.
4 этап Самостоятельная работа на 4 варианта / в группах по 4 человека/
Ученики работают с двумя листами с копировальной бумагой для последующей проверки.
1-ий вариант
Решить неравенства: Х2+8Х+7>0, и Х2-16≥0.
2.Найти ОДЗ:
2-ой вариант
Решить неравенства: Х2+10Х+21<0, и Х2-9≤0.
2.Найти ОДЗ:
3-ий вариант
Решить неравенства: 3Х2+5Х-2<0, и 5Х-Х2≤0.
2.Найти ОДЗ:
4-ий вариант
Решить неравенства: 4Х2-11Х-3≥0, и 6Х-Х2≥0.
2.Найти ОДЗ:
5 этап Подведение итогов, объявление оценок. Обобщить решение неравенств второй степени.
6 этап Дать домашнее задние с пояснением N115,121
| |
|
|
 Скачать 61.38 Kb.
Скачать 61.38 Kb.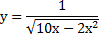
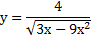
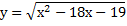
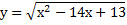
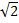 ПЛАН УРОКА-ПРЕЗЕНТАЦИИ
ПЛАН УРОКА-ПРЕЗЕНТАЦИИ