Урок алгебры в 7 б классе. Учитель : Лупашко Людмила Валентиновна Дата проведения: 22 марта 2013 г. Тема урока : Формулы сокращённого умножения. Цели урока: Обучающая
 Скачать 107.72 Kb. Скачать 107.72 Kb. |
| Муниципальное бюджетное общеобразовательное учреждение «Лицей г. Отрадное» Урок алгебры в 7 б классе. Учитель: Лупашко Людмила Валентиновна Дата проведения: 22 марта 2013 г. Тема урока: Формулы сокращённого умножения. Цели урока: Обучающая:
Развивающая:
Воспитательная:
Оборудование. Компьютер, мультимедийный проектор, экран, презентация учителя, задание для тестов, «Математической эстафеты», самостоятельной работы, индивидуальные оценочные листы. Тип урока: Урок обобщения и систематизации знаний. План урока.
Ход урока. 1.Организационный момент: -приветствие -сообщение целей и задач урока. 2.Актуализация знаний. Эпиграф к уроку: « Не бойтесь формул! Учитесь владеть этим тонким инструментом человеческого гения! В формулах увековечены ценнейшие достижения людского рода, в них заключено величие и могущество разума, его торжество над покорённой природой». Академик И.И.Артоболевский. Фронтальный опрос. На слайде презентации появляется название формулы, учащийся должен правильно записать соответствующую формулу и грамотно прочитать её. Только после этого данная формула появляется на экране, и класс сравнивает её с написанной учеником. Формулы сокращённого умножения. 1. (a+b)2=a2+2ab+b2 - квадрат суммы 2. (a-b)2=a2-2ab+b2 - квадрат разности 3. a2-b2=(a-b)(a+b) - разность квадратов 4. (a+b)3=a3+3a2b+3ab2+b3 - куб суммы 5. (a-b)3=a3-3a2b+3ab2-b3 - куб разности 6. a3+b3=(a+b)(a2-ab+b2) - сумма кубов 7. a3-b3=(a-b)(a2+ab+b2) - разность кубов Вопрос классу: -Что такое тождество? -Почему формулы сокращенного умножения называют ещё тождествами? -Как вы думаете, где в математике применяются тождества сокращенного умножения? 3.Закрепление знаний. Начиная с задания №1, каждый учащийся класса зарабатывает баллы, которые определяются количеством правильно решённых мини-задач из следующих заданий.За каждый правильный ответ – 1 балл. Задание №1 (Презентация, слайд) Каждому ряду предлагается выбрать выражения, которые тождественно равны. Выписать номера правильных ответов в тетрадь с дальнейшей самопроверкой с помощью эффектов анимации. Выберите выражения, которые тождественно равны: I ряд II ряд III ряд (m+n)2 a2-b2 (m – n)2 1) (n-m)2 1) (a-b)(a+b) 1) (n-m)2 2) (n+m)2 2) (a-b)2 2) (-n-m)2 3) (-n+m)2 3) (b+a)(a-b) 3) (m+n)2 4) (-n-m)2 4) (a+b)(b-a) 4) (n+m)2 5) (-m-n)2 5) (b-a)2 5) (-n+m)2 Задание №2 Все учащиеся делятся на два варианта. Перед ними на столах карточки с заданием. соединить линиями тождественно равные выражения. Дальнейшая проверка осуществляется с помощью эффектов анимации. Соединить линиями тождественно равные выражения Задание №2. 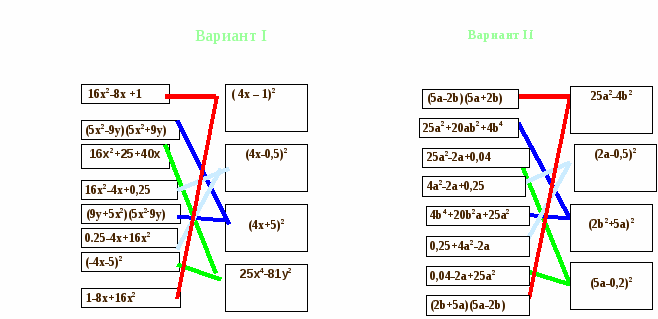 Задание №3 Данное задание выполняется в тетрадях , с дальнейшей взаимопроверкой в парах. Преобразуйте в многочлен: Вариант I Вариант II
       Задание №4 (презентация, слайд) Задание №4 (презентация, слайд)Разгадайте ребус. Учитель: «Ребята! Мне удалось зашифровать возможно новое для вас слово. Ключом к разгадке зашифрованного слова послужит правильное решение следующих задач. Каждому верно найденному значению ставится в соответствие буква русского алфавита. Ребус 1) Вычислите: Решите уравнения: 872-174•67+672 4) (1+5x) (1-5x) +25x2+x=0 2) Найдите: 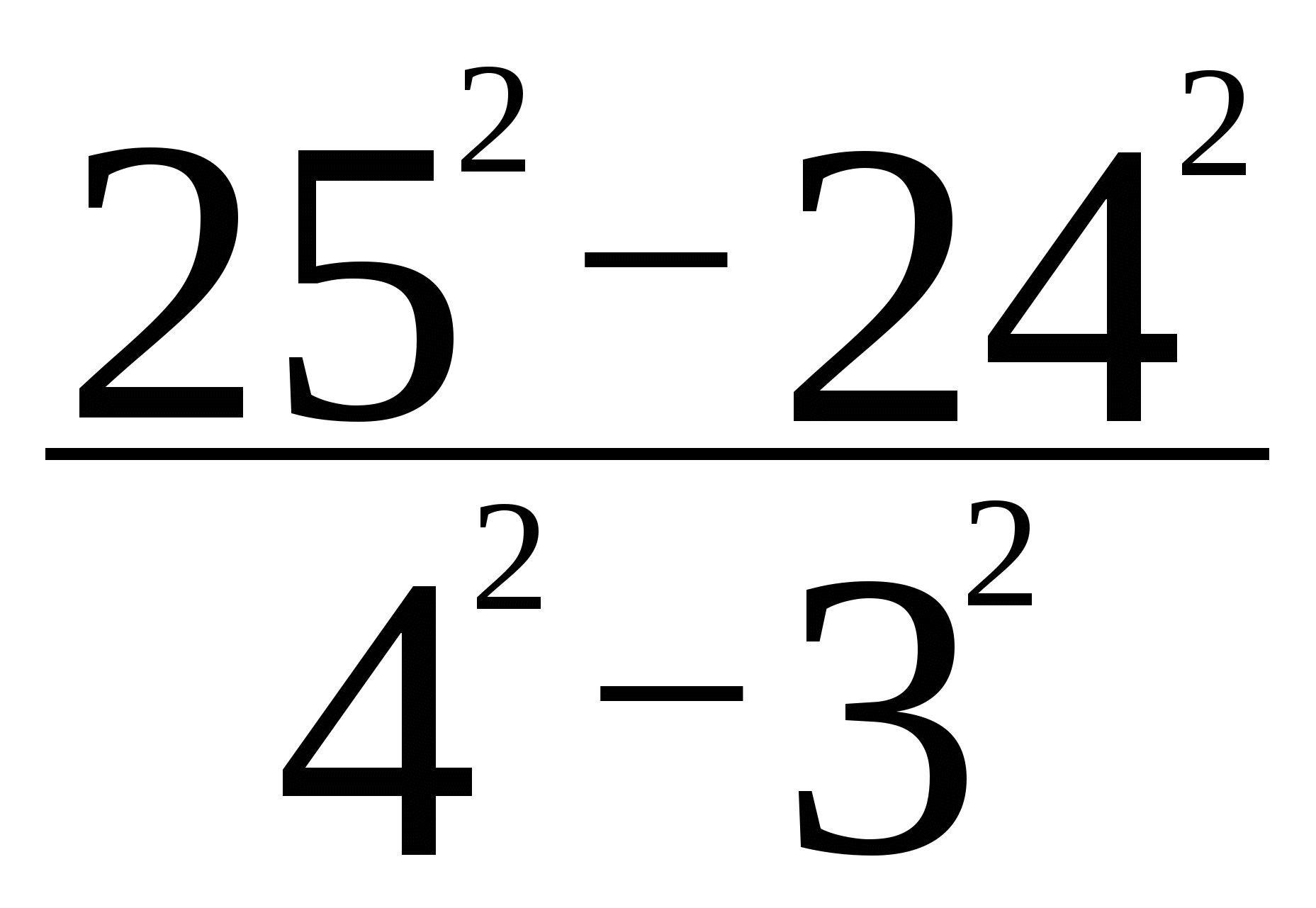 5) x(8-9x)+40=(6+3x)(6-3x) 5) x(8-9x)+40=(6+3x)(6-3x)3) Найдите: 6) (x-7)2-(x-2)(x+2)+3=0 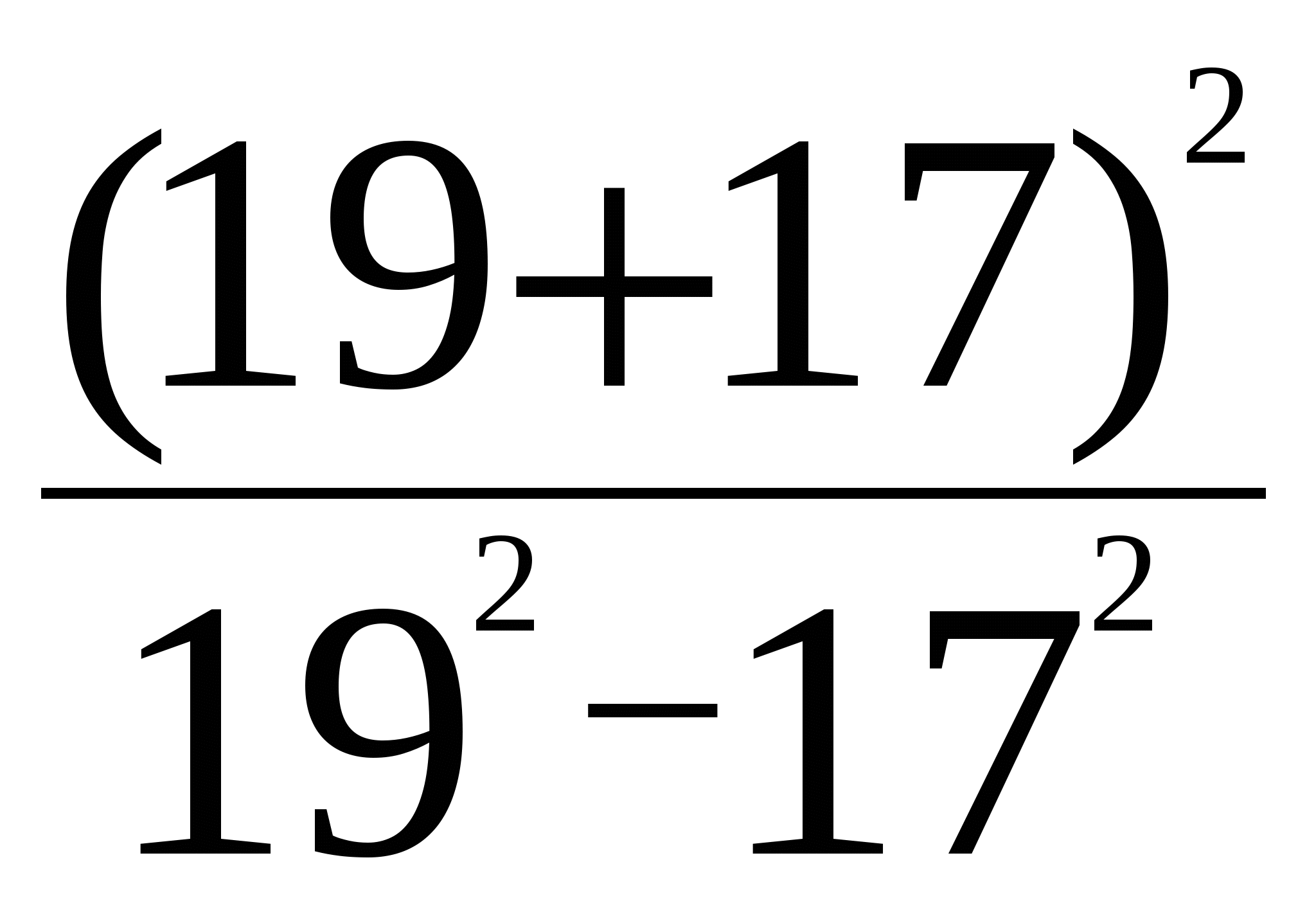
Учитель: Итак, мы отгадали загадочное слово – софизм. Что же такое софизм? Выслушиваются мнения учащихся класса. Учитель: Софизм- слово греческого происхождения, означающее хитроумную выдумку, ухищрение, головоломку. Каков бы ни был софизм, он обязательно содержит одну или несколько замаскированных ошибок. Раскрыть софизм – значит указать ошибку в приведённых рассуждениях! Разбор софизмов прежде всего развивает логическое мышление, то есть прививает навыки правильного мышления. Появляется слайд: Софизм. - это умышленно ложное умозаключение, которое имеет видимость правильного. «Правильно понятая ошибка – это путь к открытию.» И.П. Павлов Приведу пример софизма. Софизм. Все числа равны между собой. Пусть a≠ b. Возьмём тождество: a2-2ab+b2=b2-2ab+a2 Имеем: (a-b)2=(b-a)2 Отсюда a-b=b-a, или 2a=2b. Значит, a=b. В чём ошибка? Учащиеся отвечают на поставленный вопрос. 7.Запись домашнего задания. Учитель: Ребята! Ваше домашнее задание сегодня имеет творческий характер. Найти алгебраические софизмы, связанные с формулами сокращённого умножения. Выполнить задание надо на листах формата А4, данные материалы будут использованы нами в написании учебно-исследовательской работы по данной теме. Тест. Учащиеся выполняют тест с дальнейшей самопроверкой. Вариант 1. Вариант 2. 1. Упростите выражение: (m-4)2-(3-m)2 (a-3)2-(2-a)2 a) 14m-7 a) 2a-5 б)7+2n б) 5-2a в) 7-2m в) 5+2a г) 2m-7 г) -5-2a 2. Упростите выражение (2x-1)(2x+1) – (2x+3)2 (3x+1)(3x-1)-(3x-5)2 а)-12x-10 a) 25x-29 б)-8x2-3x-5 б) 9x2-25 в)8x2+12x-10 в) 30x-26 г)12x+10 г) -18x2-10 3. Разложите на множители: a4+2a2b+b2 x4-2bx2+b2 a) (a2+b)2 a) (x-b)2 б) (a2+b2)2 б) (x+b2)2 в) a4+b2 в) (x2-b)2 г) (a2-b)(a2-b) г) (x-b2)2 4. Разложите на множители: (x-5)2+(x-5)(x+5) (x-3)(x+3)+(x-3)2 a) 2x(x+5) a) 2x(x-3) б) x(x-5) б) (2+x)(x-3) в) 2x(x-5) в) (x-3)(x+4) г) (x-5)(2+x) г) (x-3)x 5. Найдите значение выражения: (x-2)2-2(x-2)(x+2)+(x+2)2 (a-5)2-2(a-5)(a+5)+(a+5)2 при x=-3/7 при x=-4/9 a) 12 a) 80 б) 16 б) -80 в) 14 в) -100 г) 18 г) 100 Проверь себя !
8.Изложение нового материала. Учитель: Итак, ребята, в решении каких задач применяются формулы сокращённого умножения? Оказывается, есть ещё один вид задач - задачи на делимость, который мы сегодня и рассмотрим. Решают вызванные к доске учащиеся и вслух комментируют решение. Задачи на делимость: 1. Докажите, что при любом натуральном значении m выражение (5m+1)2-(2m-1)2 делится на 7. 2. Докажите, что число (3p+1)2 – (3p-1)2 делится на 12 при всех натуральных значениях p. 3. Докажите, что (6x+3)2 – (6x-3)2 делится на 72 при всех натуральных значениях х. Решение: (5m+1)2-(2m-1)2=(25m2+10m+1) – - (4m2-4m+1)=25m2+10m+1-4m2+4m- -1=21m2+14m=7m(3m+2) – делится на 7, т.к. содержит множитель 7. Учитель: Формулы вида (a+b)2 , (a+b)3 являются частными случаями общей формулы, которая будет выведена в 10 классе и называется биномом (двучленом) Ньютона. Биномиальные коэффициенты можно найти с помощью треугольника Паскаля. Смотрим слайд. Бином Ньютона Треугольник Паскаля (a+b)n 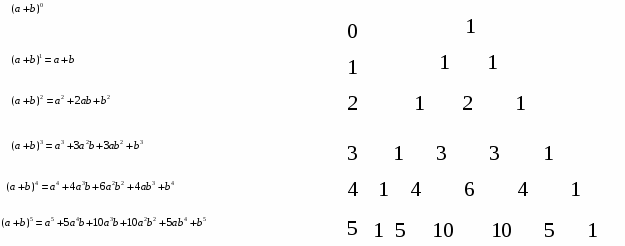 10.Подведение итогов урока. Учитель: Сегодня на уроке на примере решения вариативных задач мы рассмотрели возможные применения формул сокращённого умножения в курсе алгебры 7 класса. Какие же это применения? 1.Упрощение выражений. 2.Сокращение дробей. 3.Разложение многочлена на множители. 4. Задачи на вычисление. 5.Задачи на делимость. 6. Решение уравнений. Оценки за урок. Обменялись тетрадями и считаем сумму баллов друг друга за урок. Задание №1. 0-3 балла. Задание №2. 8 баллов. Задание №3. 5 баллов. Задание №4. 6 баллов. Задание №5 5 баллов. Максимум- 27 баллов. Критерии оценки. «5» - 25-27 баллов. «4» - 20-24 балла. «3» - 14-19 баллов. «2» - 0-13 баллов. Учитель: Поднимите, пожалуйста, руки те дети, кто сегодня за урок получил оценку 5? оценку 4? Оценку 3? Итак, сегодня на уроке на примере вариативных задач различных, как по своей фабуле, так и уровню мыслительной деятельности (на уровне синтеза, анализа, оценки, использовали задачи частично-поискового и творческого характера), мы рассмотрели возможные способы применения формул сокращённого умножения в курсе алгебры 7 класса. И в заключении... И в заключении мне хочется сказать вам: «Желаю вам успехов, ребята! Больше занимайтесь алгеброй! Помните, что решая маленькие задачи, вы готовите себя к решению больших и трудных жизненных задач!»
2 – неуверенность; 5 – радость; 7 – удовлетворение; 9 – безразличие. Учащиеся на листах бумаги пишут цифру, соответствующую их ощущениям на конец урока и показывают учителю. |