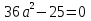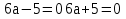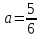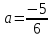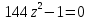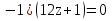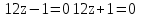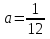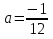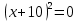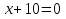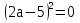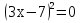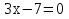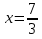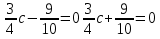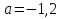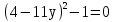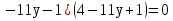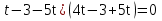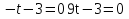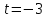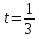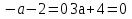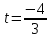Технологическая карта урока Технологическая карта урока
1. Ф.И.О. учителя: Мезенева Радмила Матвеевна
2. Класс: ____7__
3. Предмет: математика.
4. Тема урока: "Разложение на множители с помощью формул сокращенного умножения. Решение уравнений"по учебнику А.Г. Мордкович.
Цель:
Деятельностная: формирование навыков разложения многочленов на множители, умение решать уравнения.
Образовательная: создание условий для закрепление формул сокращенного умножения, умения использовать разложение на множители для решения уравнений.
Задачи:
Обучающие:
образовательные:
закрепить умение раскладывать многочлен с помощью формул сокращенного умножения;
Развивающие
развитие и мыслительной активности, используя различные формы работы;
развитие навыков самостоятельной работы;
развитие математической речи и креативности.
Воспитательные:
Тип урока: Урок рефлексии.
Оборудование: учебник, мультимедийный проектор, карточки с заданиями.
Методы:
словесный (рассуждение, беседа);
практический (выполнение самостоятельной работы);
репродуктивный (воспроизведение имеющихся знаний).
Ход урока:
№
время
|
Этапы урока
|
Деятельность учителя
|
Предполагаемая деятельность учащихся
|
УУД
|
Методический комментарий
|
1.
2 мин
|
Организационный
Задача: создать благоприятный психологический настрой на работу
|
Учитель оценивает готовность учащихся к уроку.
Знакомит с эпиграфом урока.
|
Учащиеся успокаиваются, включаются в учебную деятельность.
|
Личностные: самоопределение.
Коммуникативные: умение выказать свою точку зрения.
|
|
2.
10-15 мин
|
Актуализация знаний
Задача: актуализация опорных знаний и способов действий.
|
Устная работа
Лови ошибку
Найди соответствия
Спрашивает цели и тему урока.
Создание мотивации.
Решение теста (помоги пирату открыть сундук, найти ключ).
|
1.Учащиеся отвечают на вопросы.
2.Решение заданий
3. Решение теста.
|
Личностные:
Нравственно - этические;
выявление затруднений.
Регулятивные: целеполагание
контроль и коррекция,
самостоятельность.
Познавательные:
логические действия;
закрепление изученного материала.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.
|
|
3.
2 мин
|
Локализация знаний
|
Корректирует знания учащихся
|
Анализируют свои ошибки, сравнивают решенную работу с эталоном, корректируют знания.
|
Познавательные:
сравнение, обобщение, формулирование вывода.
Коммуникативные: сотрудничества с учителем и учениками.
|
|
4.
3 мин
|
Построение проекта выхода из затруднений.
|
Учитель предлагает уравнений вида:
a2 х2 –b2=0
a2x2+2abx+b2=0
вместе с учениками выводят алгоритм решения уравнений.
|
Решение примеров и по алгоритму.
|
Коммуникативные: постановка вопросов, инициативное сотрудничество.
Познавательные:
построение логической цепи рассуждений; отработка навыков работы по формулам сокращенного умножения.
Регулятивные: планирование, прогнозирование.
|
|
5.
3мин
|
Обобщение затруднений во внешней речи.
|
Обобщение и анализ возникших ошибок.
Учитель показывает как заполнять таблицу.
|
Решение заданий из карточек.
Проговаривают алгоритм решения уравнений с помощью формул сокращенного умножения.
|
Личностные: осознание ответственности за общее дело.
Регулятивные: контроль, оценка, коррекция.
Познавательные: умение структурировать знания, выбор наиболее эффективных способов решения примеров и задач, рефлексия способов и условий действия, выполнение действий по алгоритму, построение логической цепи рассуждений, анализ, обобщение, подведение под понятие
Коммуникативные: управление поведением партнера, контроль, коррекция, оценка действий партнера.
|
Решение примеров у доски с проговариванием.
|
6.
2 мин
|
Физкультминутка
|
Устали? Давайте немного отдохнем.
|
Учащиеся встают и выполняют определенные упражнения.
|
|
|
7.
10-13 мин
|
Самостоятельная работа в парах с самопроверкой по эталону.
|
Предлагает задания по уровням для корректировки допущенных ошибок.
|
Ребята выполняют самостоятельную работу, в случае затруднения обращаются к помощи учителя.
Дети проверяют правильность выполнения задания, оценивают себя.
|
Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения;
Личностные: самоопределение.
|
Карточки с самостоятельной работой.
Эталон.
|
8.
3 мин
|
Включение в систему знаний и повторение.
|
Индивидуальные консультации
|
Выполняют исследовательскую работу. Заполнение таблицы и вывод.
Пропедевтическое задание.
|
Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения;
Личностные: самоопределение.
|
|
9
4 мин
|
Рефлексия деятельности (итог урока)
|
Домашнее задание.
Продолжи предложение:
…
Комментирует работу учащихся на уроке.
|
Запись задания в дневниках.
Выставление самооценки за урок
|
Регулятивные: оценка-осознание уровня и качества усвоения; контроль
|

|
Сценарий урока.
1 этап. Организационный.
Здравствуйте! Давайте улыбнемся друг другу, настроимся на хорошую плодотворную работу. Сегодняшний урок мне бы хотелось начать словами Рене Декарта, он сказал: «Мало иметь хороший ум, главное - хорошо его применять». Вы согласны с Декартом?
этап. Актуализация знаний.
Индивидуальная работа. Разбор ошибки домашнего задания. Разложите на множители:
(х+1)2–25 , (у–2)2–4, х2у2–1.
Для того, чтобы узнать тему сегодняшнего урока, я предлагаю вам выполнить следующее задание: Найти соответствия между многочленом и его разложением. Полученное слово и будет подсказкой темы урока.
a2+4a+4 е. решений нет
a2 9 к. (a4 9 к. (a4 9)(a4+9) 9)(a4+9)
25x2 16 a. (5x 16 a. (5x  4)(5x+4) 4)(5x+4)
49x2 14x+1 и. (а3 14x+1 и. (а3 3)(а3+3) 3)(а3+3)
4x4 12x2y3+9y6 з. (a+4) 2 12x2y3+9y6 з. (a+4) 2
x4+49 р. (a 3)(a+3) 3)(a+3)
9y6 12x2y3+4x4 д. (x2 12x2y3+4x4 д. (x2 7)(x2+7) 7)(x2+7)
a6 9 в. (7x 9 в. (7x 1)2 1)2
a16 81 н. (2x2 81 н. (2x2 3у3)2 3у3)2
у. (a+2) 2
В: Какова же тема сегодняшнего урока? Цель урока?
Вспомним, как решаются уравнения. Поможем пирату открыть сундук, найти ключ к замку.
Решение теста. Решите уравнения.
(х+3)(х 2)=0 2)=0
а) х=3; х=2; б) х=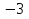 ; х=2; в) х=3; х= ; х=2; в) х=3; х=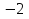 ; г) х= ; г) х=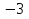 ; х= ; х= 2 2
(а+3)2=0
а) а=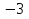 ; б) а=3; в) а=0; а=3; г) а=0; а= ; б) а=3; в) а=0; а=3; г) а=0; а=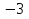
х2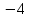 =0 =0
а) х=2; б) х=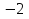 ; в) х=2; х= ; в) х=2; х=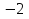 ; г) решения нет ; г) решения нет
a2 4a+4=0 4a+4=0
а) а=2; б) а=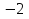 ; в) а=4; г) решения нет ; в) а=4; г) решения нет
Проверка теста. (Ответ: б, а, в, а)
Оценка за тест заносится в лист оценивания.
-
ФИО
|
ОЦЕНКА ЗА ТЕСТ
|
ОЦЕНКА ЗА УРОК
|
|
|
|
|
|
|
этап. Локализация знаний. Учащиеся анализируют свои ошибки, сравнивают решенную работу с эталоном, корректируют знания.
этап. Построение проекта выхода из затруднений.
В: Все ли уравнения легко решались. Вызвали ли какие – нибудь уравнения затруднения?
Рассмотрим подробнее эти уравнения. Разбор уравнения учеником, справившимся с заданием.
этап. Обобщение затруднений во внешней речи.
Решение 1 и 2 уравнения из карточек у доски с комментарием. Правило заполнения таблицы.
1 вариант.
-
|
уравнение
|
ответ
|
Отметка о правильности выполнения
|
Ответ
|
Отметка о правильности выполнения
|
1
|
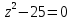
|
|
|
|
|
2
|
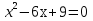
|
|
|
|
|
3
|
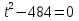
|
|
|
|
|
4
|
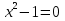
|
|
|
|
|
5
|
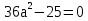
|
|
|
|
|
6
|
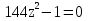
|
|
|
|
|
7
|
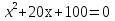
|
|
|
|
|
8
|
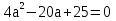
|
|
|
|
|
Эталон решения
вариант.
-
1
|
2
|
3
|
4
|
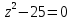
(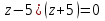
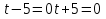
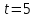 t= –5 t= –5
|
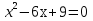
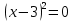
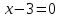
t= 3
|
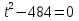
(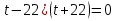
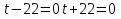
 t= –22 t= –22
|
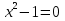
(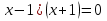
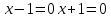
x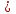 1 x= –1 1 x= –1
|
5
|
6
|
7
|
8
|
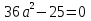
(
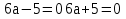
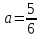 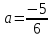
|
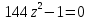
(12z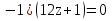
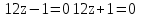
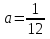 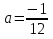
|
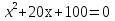
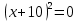
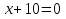
t= –10
|
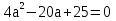
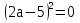
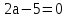
a = 2,5
|
2 вариант.
-
|
уравнение
|
ответ
|
Отметка о правильности выполнения
|
Ответ
|
Отметка о правильности выполнения
|
1
|
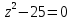
|
|
|
|
|
2
|
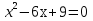
|
|
|
|
|
3
|
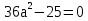
|
|
|
|
|
4
|
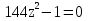
|
|
|
|
|
5
|
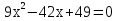
|
|
|
|
|
6
|
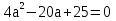
|
|
|
|
|
7
|
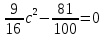
|
|
|
|
|
8
|
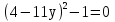
|
|
|
|
|
Эталон решения
вариант.
-
1
|
2
|
3
|
4
|
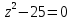
(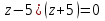
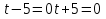
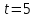 t= –5 t= –5
|
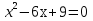
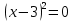
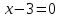
t= 3
|
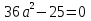
(
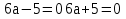
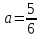 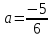
|
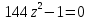
(12z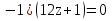
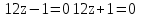
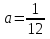 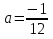
|
5
|
6
|
7
|
8
|
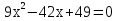
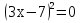
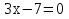
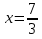
|
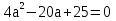
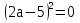
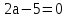
a = 2,5
|
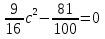
( 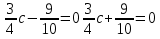
c 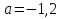
|
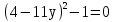
(4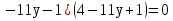
3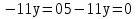
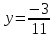 
|
3 вариант.
-
|
уравнение
|
ответ
|
Отметка о правильности выполнения
|
Ответ
|
Отметка о правильности выполнения
|
1
|
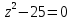
|
|
|
|
|
2
|
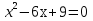
|
|
|
|
|
3
|
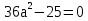
|
|
|
|
|
4
|
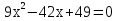
|
|
|
|
|
5
|
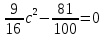
|
|
|
|
|
6
|
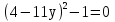
|
|
|
|
|
7
|
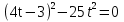
|
|
|
|
|
8
|
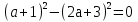
|
|
|
|
|
Эталон решения
вариант.
-
1
|
2
|
3
|
4
|
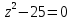
(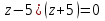
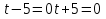
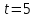 t= –5 t= –5
|
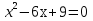
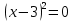
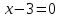
t= 3
|
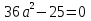
(
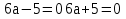
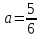 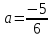
|
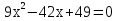
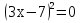
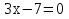
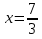
|
5
|
6
|
7
|
8
|
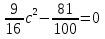
( 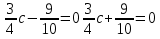
c 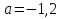
|
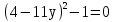
(4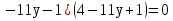
3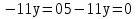
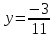 
|
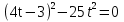
(4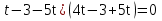
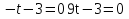
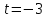 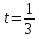
|
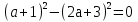
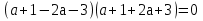
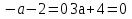
 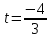
|
этап. Физкультминутка.
Мы устали, засиделись,
Нам размяться захотелось.
Отложили мы тетрадки,
Приступили мы к зарядке
(Одна рука вверх, другая вниз, рывками менять руки)
То на стену посмотрели,
То в окошко поглядели.
Вправо, влево, поворот,
А потом наоборот
(Повороты корпусом)
Головой мы повертели
И за парты дружно сели.
Дети садятся на свои места)
этап. Самостоятельная работа в парах с самопроверкой по эталону.
8 этап. Включение в систему знаний и повторение . 09.47Рассмотрим полученную таблицу. Какой вывод можно сделать, решая квадратное уравнение, которое можно свернуть по формуле сокращенного умножения? Заполним кластер. Итак, если в левой части уравнения квадратный трехчлен, который можно свернуть по формуле, то сколько корней имеет уравнение? Если в левой части квадратный двучлен, который можно свернуть по формуле, то уравнение имеет … корня. Творческое задание. 1 вариант. Для каждого выражения в строке укажите его словесное описание в столбце: ( с помощью знака v )
|
(а+в)²
|
(а-в)²
|
а²–в²
|
а²+в²
|
Квадрат суммы
|
+
|
|
|
|
Разность квадратов
|
|
|
+
|
|
Квадрат разности
|
|
+
|
|
|
Сумма квадратов
|
|
|
|
+
| 2 и 3 вариант.
m2 – 20m + ...2 = (m – ...)2
... + ... + 81=(5a + ...)2
4a2 – …=(... – 3) (... + 3)
а3–…=(а–…)(…+2а+…)
9 этап. Рефлексия деятельности.
Продолжи предложения:
Я сегодня узнал…
Сегодня на уроке я понял…
Моим самым важным открытием сегодня на уроке стало…
Сегодня мне было непонятно…
Сегодняшний урок показал мне…
После сегодняшнего урока я захотел…
Итог урока. Домашнее задание. Выставление оценок учащимися в лист контроля.
|
 Скачать 118.17 Kb.
Скачать 118.17 Kb.




 Технологическая карта урока
Технологическая карта урока  9 к. (a4
9 к. (a4 9)(a4+9)
9)(a4+9) 16 a. (5x
16 a. (5x  4)(5x+4)
4)(5x+4) 14x+1 и. (а3
14x+1 и. (а3 3)(а3+3)
3)(а3+3) 12x2y3+9y6 з. (a+4) 2
12x2y3+9y6 з. (a+4) 2 3)(a+3)
3)(a+3) 12x2y3+4x4 д. (x2
12x2y3+4x4 д. (x2 7)(x2+7)
7)(x2+7) 9 в. (7x
9 в. (7x 1)2
1)2 81 н. (2x2
81 н. (2x2 3у3)2
3у3)2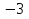 ; х=2; в) х=3; х=
; х=2; в) х=3; х=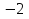 ; г) х=
; г) х=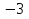 ; х=
; х= 2
2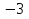 ; б) а=3; в) а=0; а=3; г) а=0; а=
; б) а=3; в) а=0; а=3; г) а=0; а=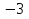
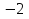 ; в) х=2; х=
; в) х=2; х=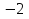 ; г) решения нет
; г) решения нет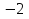 ; в) а=4; г) решения нет
; в) а=4; г) решения нет 
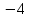 =0
=0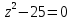
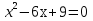
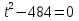
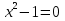
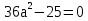
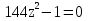
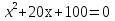
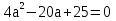
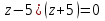
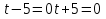
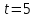 t= –5
t= –5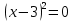
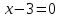
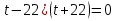
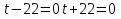
 t= –22
t= –22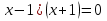
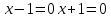
 1 x= –1
1 x= –1