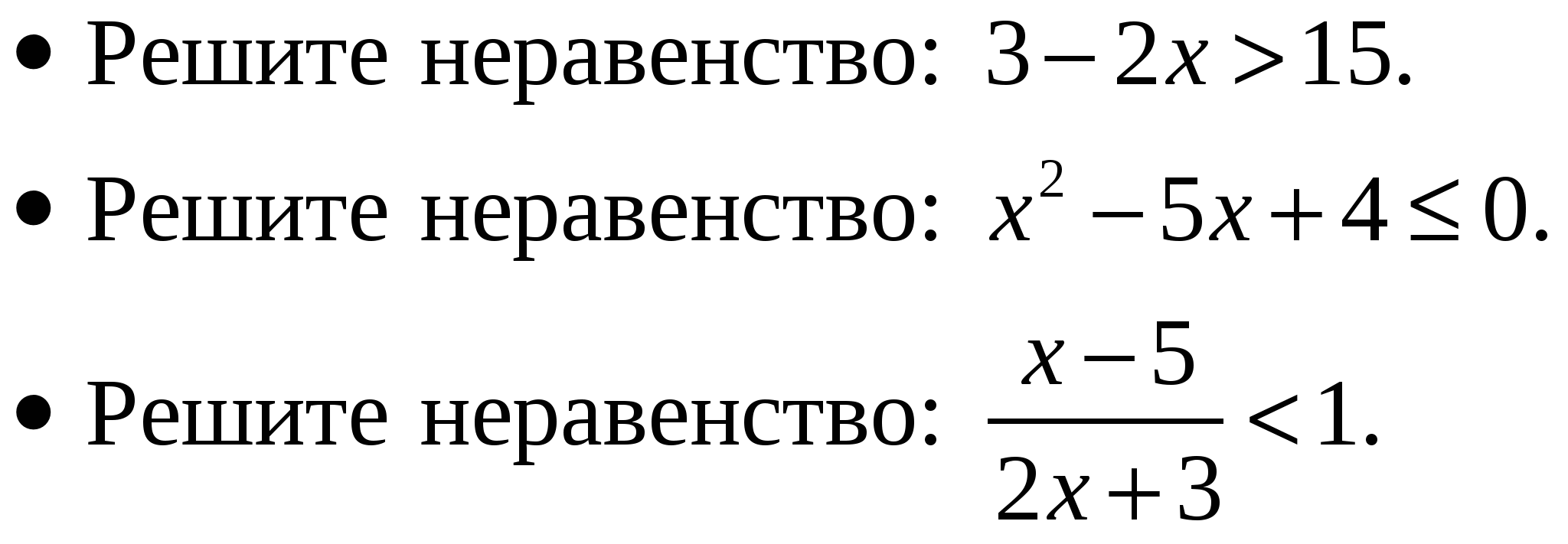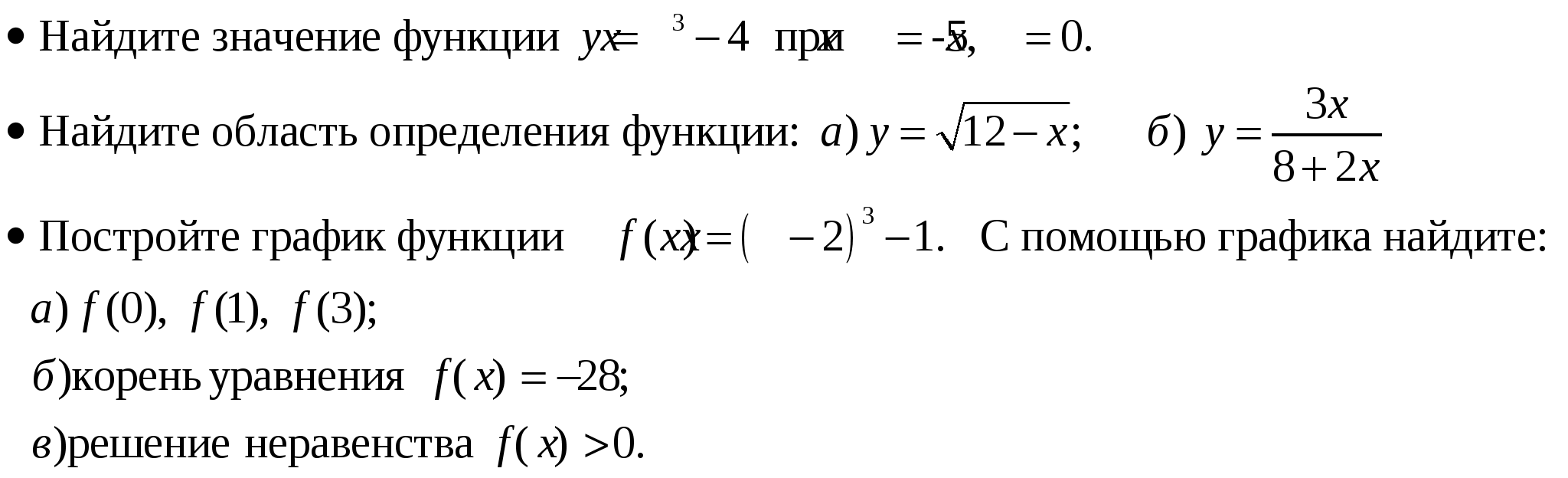|
Рабочая учебная программа по математике 9 класс Учитель: Абраменко В. А. 2011 год пояснительная записка
Муниципальное общеобразовательное учреждение
«Княжегорская средняя общеобразовательная школа»
« Рассмотрено» «Согласовано» « Утверждено»
Руководитель МО Зам. директора по УР Директор
МОУ «Княжегорская СОШ»
________/ Малинина О.М. _______ / В.А.Абраменко / __________ / Т.Н.Пронина/
«___»_____________2011г. «___»_____________2011г «___»___________2011г
Рабочая учебная программа
по математике 9 класс
Учитель: Абраменко В.А.
2011 год
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Цели обучения.
Школьное математическое образование ставит следующие цели обучения:
овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для повседневной жизни;
формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности;
формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.
Общая характеристика учебного предмета.
Математика нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык математики подчеркивает значение как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения математики является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения математики является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов, для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
Содержание рабочей программы.
В рабочей программе представлены содержание математического образования, требования к обязательному и возможному уровню подготовки обучающегося и выпускника, виды контроля, а также компьютерное обеспечение урока.
Материалы для рабочей программы составлены на основе:
федерального компонента государственного стандарта общего образования,
примерной программы по математике основного общего образования;
федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях;
с учетом требований к оснащению образовательного процесса в соответствии с содержанием наполнения учебных предметов компонента государственного стандарта общего образования;
авторского тематического планирования учебного материала;
базисного учебного плана 2004 года.
Место предмета в базисном учебном плане
Курс математики 9 класса состоит из следующих предметов: «Алгебра», «Геометрия», «Элементы логики, комбинаторики, статистики и теории вероятности», которые изучаются блоками. В соответствии с этим составлено тематическое планирование.
В соответствии с федеральным базисным учебным планом для образовательных учреждений Российской Федерации на изучение математики в 9 классе отводится 5 часов в неделю. Планирование составлено на 170 уроков (34 рабочих недели) (алгебра - 102 часов, геометрия – 68 часов).
Контрольных работ всего – 11.
Из них: по алгебре – 6, по геометрии – 4, итоговая – 1
ОСНОВНАЯ ЧАСТЬ
Тема 1 «Неравенства и системы неравенств» (13 часов)
Раздел математики. Сквозная линия
Уравнения и неравенства.
Обязательный минимум содержания образовательной области математика
Числовые неравенства и их свойства.
Линейные неравенства с одной переменной.
Решение неравенства.
Квадратные неравенства.
Рациональные неравенства.
Системы неравенств.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь решать линейные неравенства с одной переменной.
Уметь решать квадратные неравенства.
Уметь решать рациональные неравенства.
Уметь решать системы неравенства.
Уровень возможной подготовки обучающегося
Уметь решать линейные, квадратные, рациональные неравенства и их системы.
Знать как используются неравенства; примеры их применения для решения математических и практических задач.
Уметь решать неравенства с модулем.
Уровень обязательной подготовки выпускника
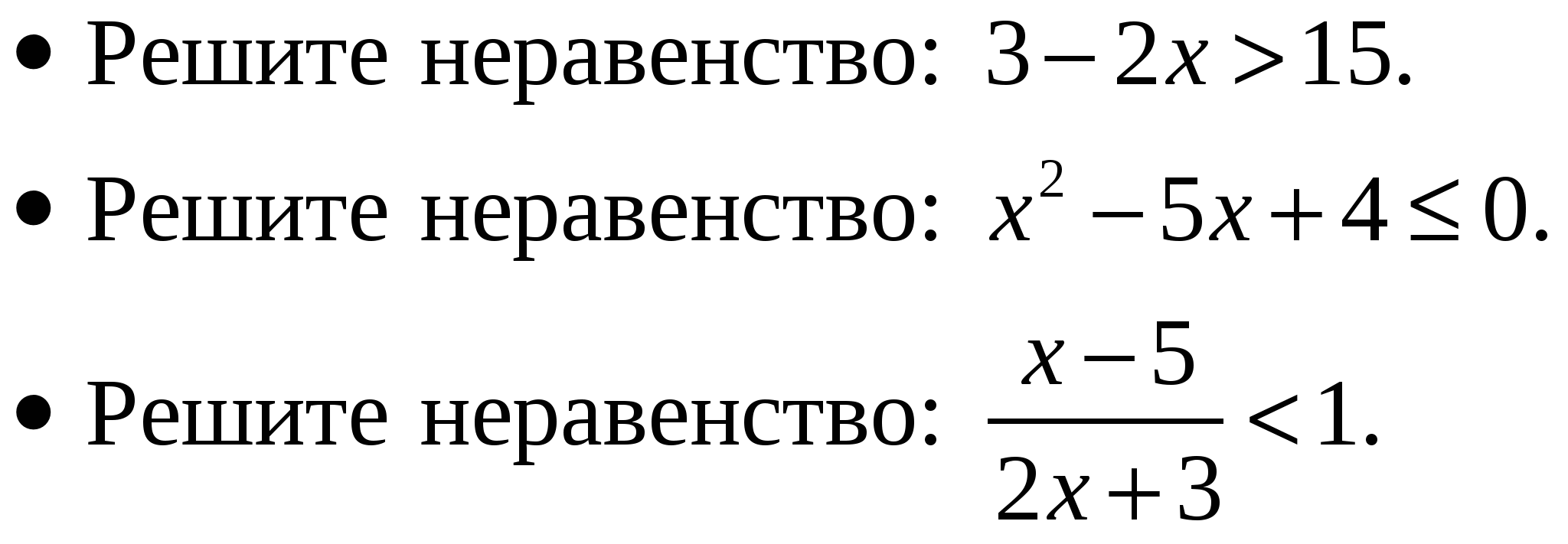
Уровень возможной подготовки выпускника

Тема 2 «Вводное повторение» (2 часа).
«Векторы. Метод координат» (19 часов)
Раздел математики. Сквозная линия.
Геометрические фигуры и их свойства.
Измерение геометрических величин.
Обязательный минимум содержания образовательной области математика
Вектор. Откладывание вектора от данной точки. Длина (модуль) вектора.
Коллинеарные и равные векторы.
Операции над векторами: сложение и вычитание векторов, умножение вектора на число на число.
Средняя линия трапеции.
Вектор. Длина (модуль) вектора. Равенство векторов.
Координаты вектора.
Операции над векторами: умножение вектора на число, сложение, разложение.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь пользоваться языком геометрии для описания предметов окружающего мира.
Уметь производить операции над векторами.
Уметь вычислять значения геометрических величин.
Уметь решать геометрические задачи с применением векторов.
Уметь решать геометрические задачи координатным методом.
Уровень возможной подготовки обучающегося
Уметь пользоваться языком геометрии для описания предметов окружающего мира.
Уметь производить операции над векторами.
Уметь вычислять значения геометрических величин.
Уметь решать геометрические задачи с применением векторов.
Уметь проводить доказательные рассуждения при решении задач, используя известные теоремы.
Уметь решать простейшие планиметрические задачи в пространстве.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни.
Уровень подготовки выпускника
Знать и понимать:
понятия вектора, нулевого вектора, длины вектора, коллинеарных векторов, равенства векторов;
операции над векторами в геометрической форме (правило треугольника, правило параллелограмма, правило многоугольника, правило построения разности векторов и вектора, получающегося при умножении вектора на число);
законы сложения векторов, умножения вектора на число;
формулу для вычисления средней линии трапеции.
Уметь:
откладывать вектор от данной точки;
пользоваться правилами при построении суммы, разности векторов; вектора, получающегося при умножении вектора на число;
применять векторы к решению задач;
находить среднюю линию треугольника;
раскладывать вектор.
Уровень обязательной подготовки выпускника

Уровень возможной подготовки выпускника

Тема 3 «Системы уравнений» (15 часов)
Раздел математики. Сквозная линия
Обязательный минимум содержания образовательной области математика
Уравнение с двумя переменными; решение уравнения с двумя переменными.
Система уравнений; решение систем уравнений.
Система двух линейных уравнений с двумя переменными.
Решение систем уравнений подстановкой.
Решение систем уравнений алгебраическим сложением.
Решение нелинейных систем уравнений.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь решать несложные нелинейные системы уравнений.
Уметь решать текстовые задачи алгебраическим методом с помощью систем уравнений, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи.
Уровень возможной подготовки обучающегося
Уметь решать нелинейные системы уравнений различными методами.
Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни для моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры.
Уметь строить графики уравнений с двумя неизвестными.
Уметь решать неравенства и системы неравенств с двумя неизвестными.
Уровень обязательной подготовки выпускника

Уровень возможной подготовки выпускника

Тема 4 «Соотношения между сторонами и углами треугольника. Скалярное произведение векторов» (14 часов)
Раздел математики. Сквозная линия
Геометрические фигуры и их свойства.
Измерение геометрических величин.
Обязательный минимум содержания образовательной области математика
Синус, косинус и тангенс углов от 0о до 180о.
Теорема синусов и теорема косинусов. Примеры их применения для вычисления элементов треугольника.
Формула, выражающая площадь треугольника через две стороны и угол между ними.
Скалярное произведение векторов.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь производить операции над векторами, вычислять длину и координаты вектора, угол между векторами, скалярное произведение.
Уметь вычислять значения геометрических величин, в том числе: для углов от 0о до 180о определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них; находить стороны, углы и площади треугольников.
Уровень возможной подготовки обучающегося
Уметь пользоваться языком геометрии для описания предметов окружающего мира.
Уметь производить операции над векторами.
Уметь вычислять значения геометрических величин.
Уметь решать геометрические задачи, применяя тригонометрические функции и скалярное произведение.
Уметь проводить доказательные рассуждения при решении задач, используя известные теоремы.
Уметь решать простейшие планиметрические задачи в пространстве, используя скалярное произведение векторов.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни.
Уровень обязательной подготовки выпускника

Уровень возможной подготовки выпускника
Тема 5 «Числовая функция» (25 часов)
Раздел математики. Сквозная линия
Функция
Обязательный минимум содержания образовательной области математика
Понятие функции. Область определения и область значений функции.
Способы задания функции.
График функции, возрастание и убывание функции, наибольшее и наименьшее значения функции, нули функции, промежутки знакопостоянства.
Четные и нечетные функции.
Степенные функции с натуральным и целым показателем, их свойства и графики.
Функция 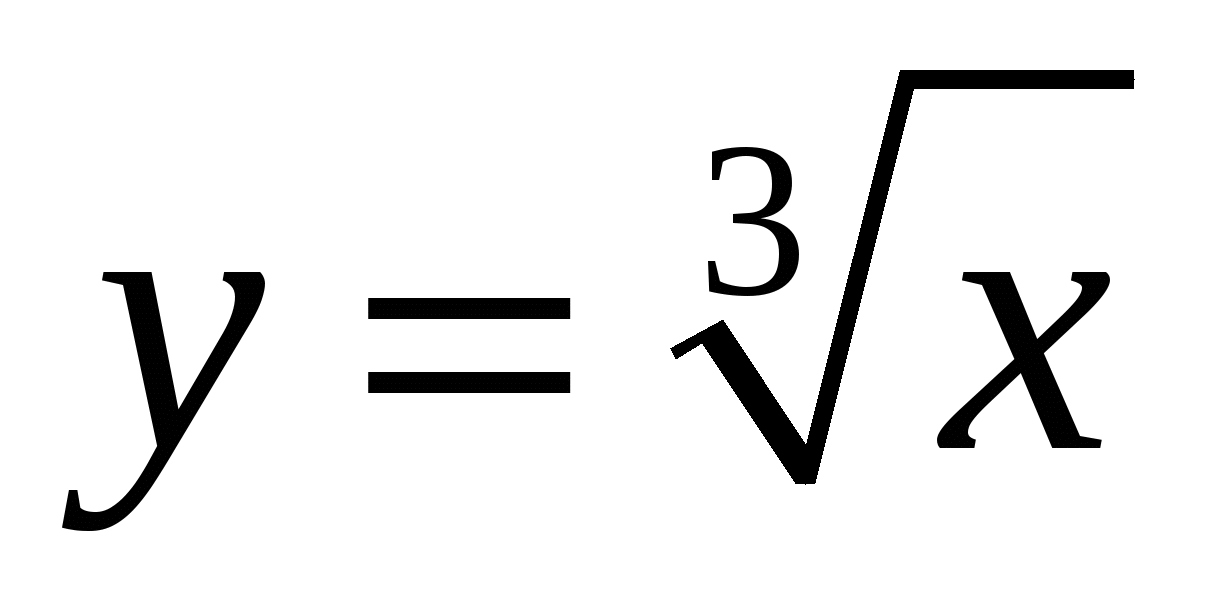 , ее свойства и график , ее свойства и график
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь находить значения функции, заданной формулой, таблицей, графиком по ее аргументу.
Уметь находить значение аргумента по значению функции, заданной графиком или таблицей.
Уметь определять свойства квадратичной функции по ее графику.
Уметь описывать свойства квадратичной функции, строить ее график.
Знать свойства степенной функции с натуральным и целым показателем.
Знать свойства функции 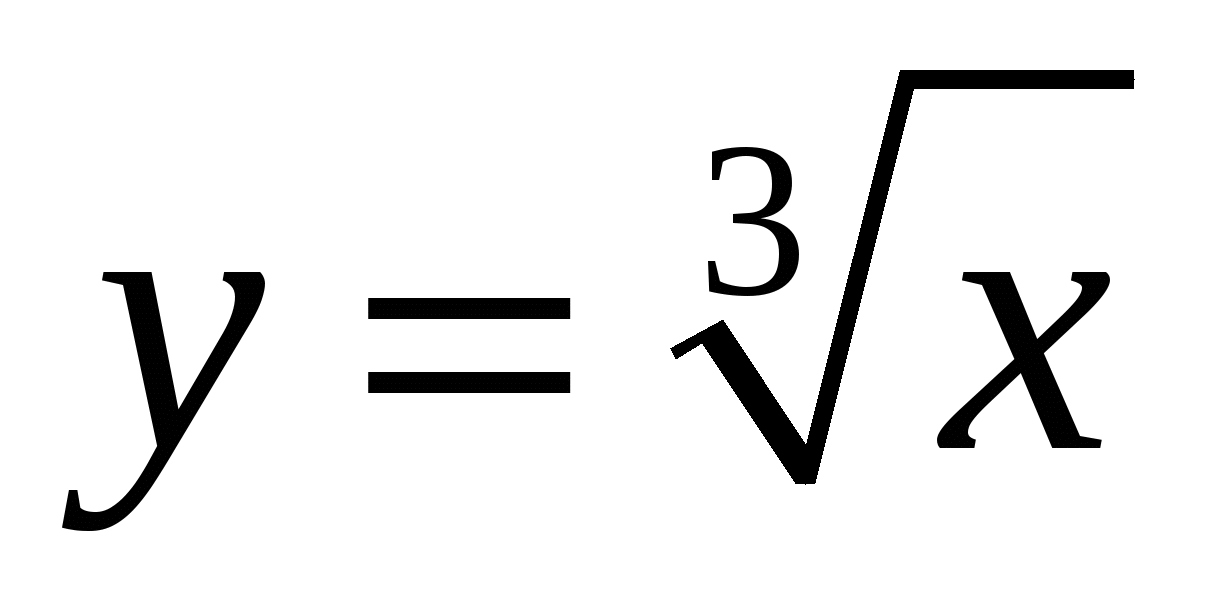 . .
Уровень возможной подготовки обучающегося
Понимать, что функция – это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами.
Уметь определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств.
Уметь строить графики различных функций с помощью параллельных переносов.
Уметь интерпретировать в несложных случаях графики реальных зависимостей между величинами, отвечая на поставленные вопросы.
Уровень обязательной подготовки выпускника 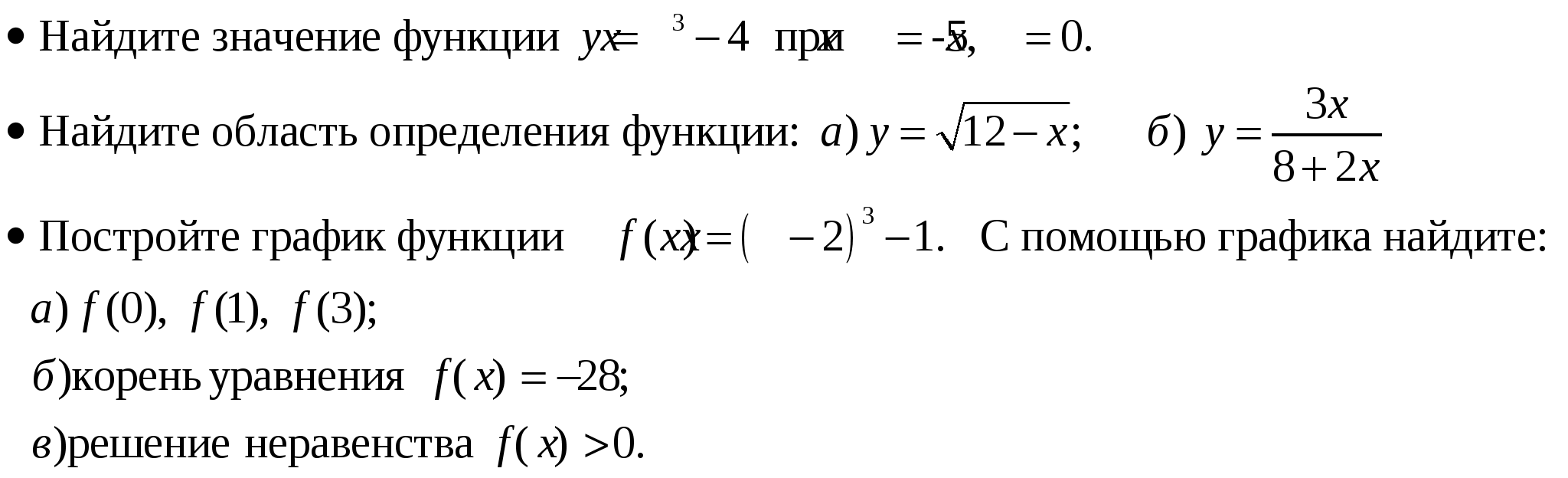
Уровень возможной подготовки выпускника

Тема 6 «Длина окружности и площадь круга» (12 часов)
Раздел математики. Сквозная линия
Геометрические фигуры и их свойства.
Измерение геометрических величин.
Обязательный минимум содержания образовательной области математика
Вписанные и описанные многоугольники. Правильные многоугольники. Сумма углов правильного многоугольника.
Длина окружности, число π; длина дуги.
Площадь круга и площадь сектора.
Вписанные и описанные окружности правильного многоугольника.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь пользоваться языком геометрии для описания предметов окружающего мира.
Уметь распознавать геометрические фигуры, различать их взаимное расположение.
Уметь изображать геометрические фигуры; Выполнять чертежи по условию задачи.
Уметь вычислять длины дуг окружности, длину окружности, периметры и площади правильных многоугольников, площади круга и сектора.
Уровень возможной подготовки обучающегося
Уметь проводить доказательные рассуждения при решении задач, используя известные теоремы.
Уметь решать простейшие планиметрические задачи в пространстве.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для решения практических задач, связанных с нахождением геометрических величин(используя при необходимости справочники и технические средства.
Уметь выполнять построения правильных многоугольников.
Уровень обязательной подготовки выпускника
Сколько сторон имеет правильный многоугольник, если каждый его угол равен а) 60о; б)135о; в) 150о?
Найдите площадь правильного восьмиугольника, если радиус его вписанной окружности равен 6 см.
Найдите длину дуги окружности радиуса 12 см, если ее градусная мера равна 60о.
Длина окружности цирковой арены равна 41 м. Найдите диаметр и площадь арены.
Уровень возможной подготовки выпускника
В круг, площадь которого равна 36π см2, вписан правильный шестиугольник. Найдите сторону шестиугольника и его площадь.
Постройте правильный восьмиугольник, сторона которого равна данному отрезку.
Даны два круга. Постройте круг, площадь которого равна сумме площадей данных кругов.
Тема 7 «Прогрессии» (16 часов)
Раздел математики. Сквозная линия
Вычисления и числа.
Выражения и преобразования.
Обязательный минимум содержания образовательной области математика
Понятие последовательности.
Арифметическая и геометрическая прогрессии.
Формулы общего члена арифметической и геометрической прогрессий.
Формулы суммы первых нескольких членов арифметической и геометрической прогрессий.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Распознавать арифметические и геометрические прогрессии.
Решать несложные задачи с применением формул общего члена и суммы нескольких первых членов прогрессий.
Уровень возможной подготовки обучающегося
Понимать смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.
Распознавать арифметические и геометрические прогрессии.
Решать задачи с применением формул общего члена и нескольких первых членов прогрессий.
Уровень обязательной подготовки выпускника

Уровень возможной подготовки выпускника

Тема 8 «Движение» (10 часов)
Тема 9 «Об аксиомах геометрии (1 час)
Раздел математики. Сквозная линия
Геометрические фигуры и их свойства.
Измерение геометрических величин.
Обязательный минимум содержания образовательной области математика
Материал подлежит изучению, но не включается в Требования к уровню подготовки учеников.
Требования к математической подготовке
Уровень возможной подготовки обучающегося
Примеры движения фигур.
Центральная и осевая симметрия.
Параллельный перенос.
Поворот.
Уровень возможной подготовки выпускника
Даны точка О и треугольник АВС. Постройте фигуру F, на которую отображается треугольник АВС при центральной симметрии с центром О. Что представляет собой фигура F?
Постройте треугольник, который получается из данного треугольника АВС поворотом вокруг точки А на угол 160о против часовой стрелки.
Тема 10 «Элементы комбинаторики, статистики и теории вероятностей»
(12 часов)
Раздел математики. Сквозная линия
Числа и вычисления.
Множества и комбинаторика.
Статистика.
Вероятность.
Обязательный минимум содержания образовательной области математика
Примеры решения комбинаторных задач: перебор вариантов, правило умножения.
Примеры решения комбинаторных задач: перебор вариантов, правило умножения.
Представление данных в виде таблиц, диаграмм, графиков.
Средние значения результатов измерений.
Понятие о статистическом выводе на основе выборки.
Понятие и примеры случайных событий.
Частота события, вероятность случайного события.
Требования к математической подготовке
Уровень обязательной подготовки обучающегося
Уметь решать комбинаторные задачи путем систематического перебора возможных вариантов.
Уметь решать комбинаторные задачи с использованием правила умножения;
Уметь извлекать информацию, представленную в таблицах, на диаграммах, графиках.
Уметь составлять таблицы, строить диаграммы, графики.
Уметь вычислять средние значения результатов измерений.
Уметь находить вероятности случайных событий в простейших случаях.
Уровень возможной подготовки обучающегося
Уметь находить частоту события, используя собственные наблюдения и готовые статистические данные.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для решения учебных и практических задач, требующих систематического перебора вариантов.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для сравнения шансов наступления случайных событий, оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией.
Понимать различные статистические утверждения.
Уровень обязательной подготовки выпускника
Сколькими способами могут разместиться 6 человек в салоне автобуса на шести свободных местах?
Сколько трехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр 1, 2, 3, 4, 5?
Из 12 членов туристической группы надо выбрать трех дежурных. Сколькими способами можно сделать такой выбор?
Какова вероятность того, что при бросании игрального кубика выпадет более 4 очков?
В таблице показан расход электроэнергии некоторой семьей в течение года:
Месяц
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
Расход электроэнергии, квтч
|
85
|
80
|
74
|
62
|
54
|
68
|
58
|
54
|
58
|
64
|
74
|
86
|
Построить столбчатую диаграмму расходов электроэнергии семьи в течение года.
Уровень возможной подготовки выпускника
Из 20 вопросов к экзамену Вова 12 вопросов выучил, 5 совсем не смотрел, а в остальных что-то знает, а что-то нет. На экзамене в билете будет три вопроса.
а) Сколько существует вариантов билетов?
б) Сколько из них тех, в которых Вова знает все вопросы?
в) Сколько из них тех, в которых есть вопросы всех трех типов?
г) Сколько из них тех, в которых Вова выучил большинство вопросов?
Случайным образом одновременно выбирают две буквы из 33 букв русского алфавита. Найдите вероятность того, что:
а) обе они гласные;
б) среди них есть буква «ь»;
в) среди них нет буквы «а»;
г) одна буква гласная, а другая согласная.
Тема 11 «Итоговое повторение. Решение задач» (29 часов)
Раздел математики. Сквозная линия
Числа и вычисления.
Выражения и преобразования.
Уравнения и неравенства.
Функции.
Геометрические фигуры и их свойства.
Измерение геометрических величин.
Обязательный минимум содержания образовательной области математика
Арифметические действия с рациональными числами.
Преобразования многочленов, алгебраических дробей. Свойства степени с натуральным показателем. Прогрессии.
Уравнение с одной переменной. Системы уравнений. Неравенства с одной переменной и их системы.
Функции: у = kx, y=kx+b, 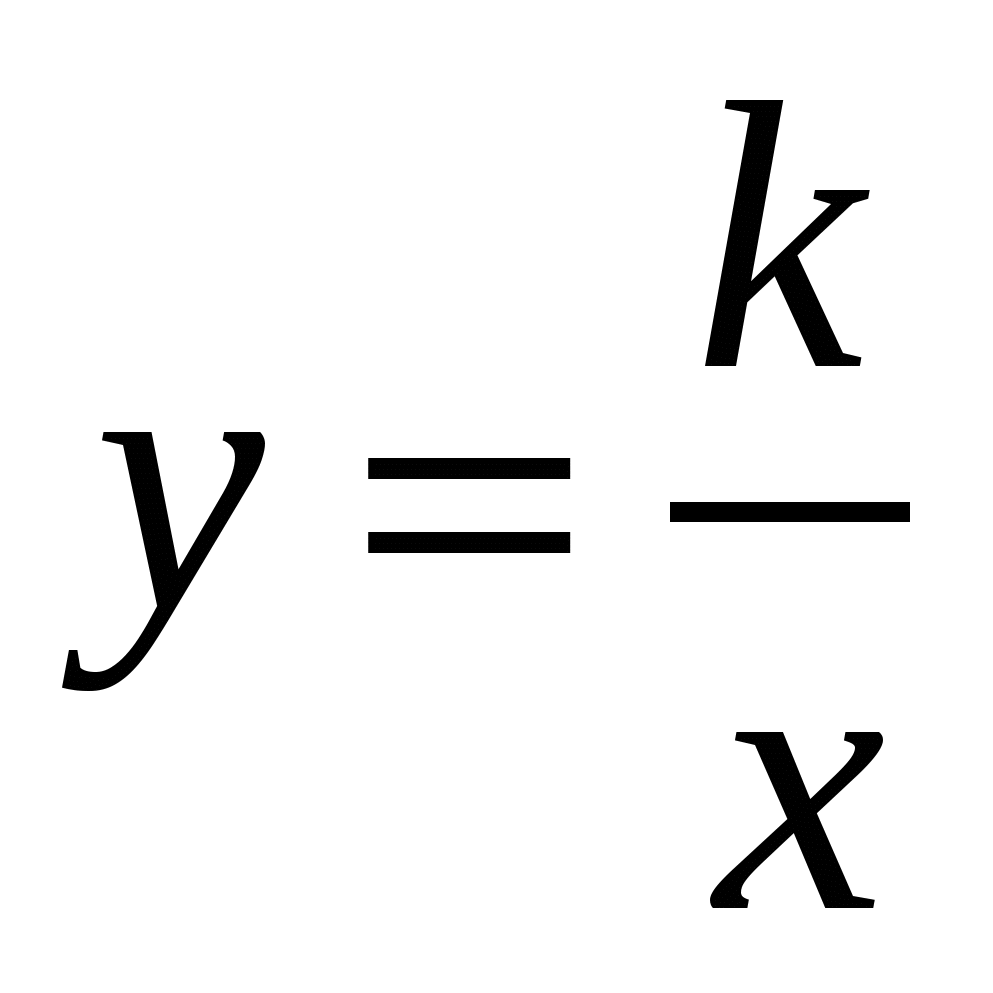 , y= x2, y= x3, у= хn, y= ax2+bx+c, их свойства и графики. , y= x2, y= x3, у= хn, y= ax2+bx+c, их свойства и графики.
Начальные понятия и теоремы геометрии
Треугольник, его свойства. Равенство и подобие треугольников. Решение треугольника.
Четырехугольники и многоугольники.
Окружность и круг.
Измерение геометрических величин.
Векторы.
Требования к математической подготовке
Уровень обязательной подготовки выпускника


Как проверить, что выпиленная из листа фанеры фигура является прямоугольником?
Начертите три неразвернутых угла и обозначьте каждый из них одним из трех способов.
С помощью транспортира найдите градусные меры углов треугольника АВС. (Задан чертеж треугольника АВС).
В равностороннем треугольнике АВС проведены биссектрисы АК и АМ, которые пересекаются в точке О. Найдите углы треугольника АОМ.
Докажите, что в равнобокой трапеции диагонали равны.
Разделите данный отрезок пополам с помощью циркуля и линейки.
Уровень возможной подготовки выпускника

В ромбе высота, проведенная из вершины тупого угла, делит его сторону пополам. Найдите: а) углы ромба; б) его периметр, если меньшая диагональ равна 3,5 см.
Хорда окружности пересекает ее диаметр под углом 30о и делится им на части, равные 12 см и 6 см. Найдите расстояние от середины хорды до диаметра.
Дан луч ОА. Постройте фигуру, центрально-симметричную ему относительно точки О. Что это за фигура?
Как расположены относительно друг друга две окружности (О1; R1) и (О2; R2), если О1О2 = 2 см, R1 = 4 см и R2 = 6 см?
Постройте треугольник по стороне, опущенной на нее высоте и прилежащему к ней углу.
Литература
Дорофеев Г. В. и др. Оценка качества подготовки выпускников основной школы по математике. М., «Дрофа», 2001.
Концепция математического образования (проект)//Математика в школе.- 2000. – № 2. – с.13-18.
Концепция модернизации российского образования на период до 2010// «Вестник образования» -2002- № 6 - с.11-40.
Мордкович А.Г., Семенов П.В. Алгебра. Учебник для 9 класса общеобразовательных учреждений. Часть 1. М., «Мнемозина», 2011.
Мордкович А.Г., Александрова Л.А. и др. Алгебра. Учебник для 9 класса общеобразовательных учреждений. Часть 2. М., «Мнемозина», 2011.
Атанасян Л.С. Геометрия 7 – 9. Учебник для 7 – 9 классов средней школы. М., «Просвещение», 2006.
Кузнецова Г.М., Миндюк Н.Г. Программы для общеобразовательных школ, гимназий, лицеев. Математика 5 – 11 классы. М., «Дрофа», 2003.
Стандарт основного общего образования по математике//«Вестник образования» -2004 - № 12 - с.107-119.
Электронные учебные пособия
Математика. Практикум. 5-11 классы. Электронное учебное издание. М., ООО «Дрофа», ООО «ДОС», 2003.
|
|
|
 Скачать 188.05 Kb.
Скачать 188.05 Kb.