Рабочая программа по предмету геометрия 9 класс кол-во часов 68 за год, 2ч в неделю

1. 
   «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования». Приказ Министерства образования Российской федерации от 5.03.2004г. №1089
   
2. 
   Федеральный компонент государственного стандарта основного общего образования. Стандарт основного общего образования по математике.// Вестник образования России, 2004, №12, стр.111-118.
   
3. 
   «Об утверждении федерального базисного учебного плана и примерных учебных планов для образовательных учреждений Российской Федерации, реализующих программы общего образования». Приказ Министерства образования Российской федерации от 5.03.2004г. №1089
   
4. 
   «Об утверждении федерального государственного образовательного стандарта основного общего образования». Приказ Министерства образования Российской федерации от 17.12.2010 года № 1897.
   
5. 
   «Об утверждении федеральных перечней учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию, на 2012\2013 учебный год». Приказ Министерства образования Российской федерации от 27.12.2011 года № 2885.
   
6. 
   Программы общеобразовательных учреждений. Геометрия. 7-9 классы. Составитель – Бурмистрова Т.А. – М.: Просвещение, 2009 г.
   
7. 
   Закон «Об образовании» РФ.
   

1. 
   в направлении личностного развития:
   

• 
  развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;
  
• 
  формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;
  
• 
  воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
  

• 
  формирование представлений о геометрии как части общечеловеческой культуры, о значимости геометрии в развитии цивилизации и современного общества;
  
• 
  развитие представлений о геометрии как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;
  
• 
  формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;
  

3. 
   в предметном направлении:
   

• 
  овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;
  
• 
  развитие пространственного воображения и логического мышления путем систематического изучения свойств геометрических фигур на плоскости и в пространстве и применения этих свойств при решении задач вычислительного и конструктивного характера;
  
• 
  развитие геометрической интуиции.
  

• 
  формирование ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учётом устойчивых познавательных интересов;
  
• 
  формирование целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;
  
• 
  формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, общественно полезной, учебно-исследовательской, творческой и других видах деятельности;
  
• 
  умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
  
• 
  критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
  
• 
  креативность мышления, инициативу, находчивость, активность при решении геометрических задач;
  
• 
  умение контролировать процесс и результат учебной математической деятельности;
  
• 
  способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
  

• 
  умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
  
• 
  умение осуществлять контроль по результату и по способу
  действия на уровне произвольного внимания и вносить не-
  обходимые коррективы;
  
• 
  умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
  
• 
  осознанное владение логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев, установления родовидовых связей;
  
• 
  умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и выводы;
  
• 
  умение создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
  
• 
  умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, общие способы работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё
  мнение;
  
• 
  формирование и развитие учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
  
• 
  первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
  
• 
  умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
  
• 
  умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
  
• 
  умение понимать и использовать математические средства
  наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
  
• 
  умение выдвигать гипотезы при решении учебных задач
  и понимать необходимость их проверки;
  
• 
  умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
  
• 
  понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
  
• 
  умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
  
• 
  умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
  

• 
  овладение базовым понятийным аппаратом по основным
  разделам содержания; представление об основных изучаемых понятиях (число, геометрическая фигура, вектор, координаты) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
  
• 
  умение работать с геометрическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить
  классификации, логические обоснования, доказательства
  математических утверждений;
  
• 
  овладение навыками устных, письменных, инструментальных вычислений;
  
• 
  овладение геометрическим языком, умение использовать
  его для описания предметов окружающего мира, развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;
  
• 
  усвоение систематических знаний о плоских фигурах и их
  свойствах, а также на наглядном уровне – о простейших пространственных телах, умение применять систематические знания о них для решения геометрических и практических задач;
  
• 
  умение измерять длины отрезков, величины углов, использовать формулы для нахождения периметров, площадей и объёмов геометрических фигур;
  
• 
  умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютера.
  

1. 
   Уроки геометрии Кирилла и Мефодия. (Виртуальная школа К и М).
   

2. 
   Открытая математика. Планиметрия. Версия 2.6. Интерактивный
   

3. 
   Интерактивная математика. Электронное учебное пособие. 5-9 кл. (CD-ROM)
   

ТРЕБОВАНИЯ К УРОВНЮ
ПОДГОТОВКИ ВЫПУСКНИКОВ

• 
  существо понятия математического доказательства; примеры доказательств;
  
• 
  существо понятия алгоритма; примеры алгоритмов;
  
• 
  как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
  
• 
  каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
  
• 
  смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
  

• 
  пользоваться языком геометрии для описания предметов окружающего мира;
  
• 
  распознавать геометрические фигуры, различать их взаимное расположение;
  
• 
  изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;
  
• 
  распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
  
• 
  в простейших случаях строить сечения и развертки пространственных тел;
  
• 
  проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;
  
• 
  вычислять значения геометрических величин (длин, углов, площадей, объемов), в том числе: для углов от 0 до 180 определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
  
• 
  решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, идеи симметрии;
  
• 
  проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
  
• 
  решать простейшие планиметрические задачи в пространстве;
  

• 
  описания реальных ситуаций на языке геометрии;
  
• 
  расчетов, включающих простейшие тригонометрические формулы;
  
• 
  решения геометрических задач с использованием тригонометрии
  
• 
  решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
  
• 
  построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
  

№№	Вопросы	Варианты ответов
1	Трапеция – это четырехугольник, у которого…	А) все стороны равны; Б) стороны попарно равны; В) две стороны параллельны, а две другие непараллельны; Г) нет правильного ответа.
2	Четырехугольник является параллелограммом, если…	А) стороны попарно равны; Б) диагонали равны; В) все углы равны; Г) нет правильного ответа.
3	Ромб с диагоналями d1 и d2 . Какова его площадь?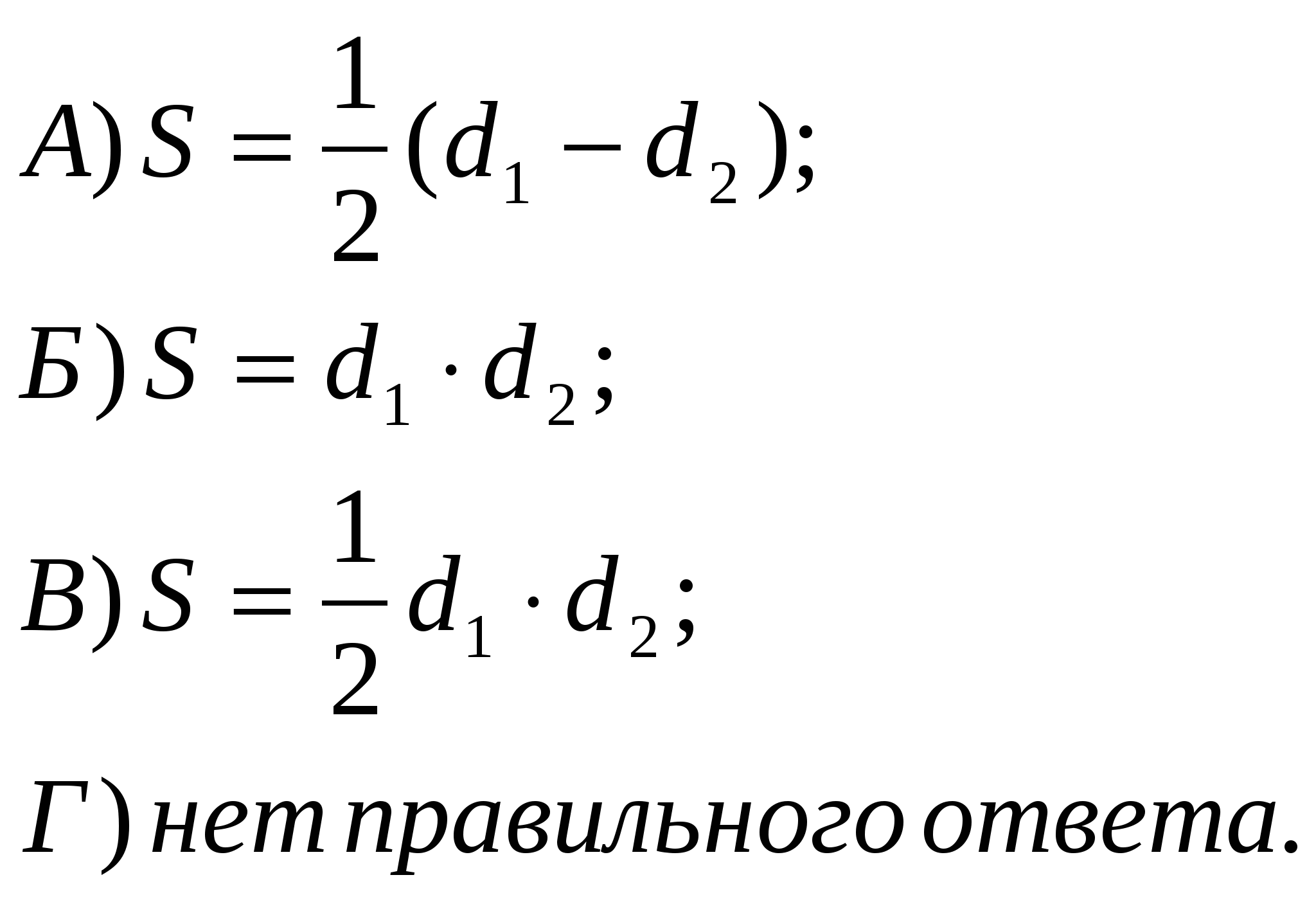
4	В прямоугольном треугольнике квадрат гипотенузы равен …	А) разности гипотенузы и катета; Б) сумме катетов; В) сумме квадратов катетов; Г) нет правильного ответа.
5	Если вершина угла лежит в центре окружности, то это…	А) центральный угол; Б) вписанный угол; В) прямой угол; Г) нет правильного ответа.
6	Треугольники называются подобными, если…	А) все углы равны; Б) стороны пропорциональны; В) углы равны и сходственные стороны пропорциональны; Г) нет правильного ответа.
7	Отрезок, соединяющий середины двух сторон треугольника, называется…	А) медианой; Б) средней линией; В) высотой; Г) нет правильного ответа.
8	Синус острого угла прямоугольного треугольника – это отношение…	А) противолежащего катета к гипотенузе; Б) гипотенузы к противолежащему катету; В) катетов; Г) нет правильного ответа.
9	Диагонали прямоугольника …	А) равны и точкой пересечения делятся пополам; Б) перпендикулярны; В) параллельны; Г) нет правильного ответа.
10	Найдите стороны параллелограмма, если одна из них на 4 см больше другой, а периметр параллелограмма равен 38 см.
11	Найдите основание равнобедренного треугольника, если боковая сторона равна 13 см, а медиана, проведенная к основанию, равна 5 см.

№№	Вопросы	Варианты ответов
1	Прямоугольник – это параллелограмм, у которого …	А) все стороны равны; Б) все углы прямые; В) диагонали перпендикулярны; Г) нет правильного ответа.
2	Четырехугольник является параллелограммом, если …	А) противоположные углы равны; Б) две стороны равны и параллельны; В) диагонали перпендикулярны; Г) нет правильного ответа.
3	В параллелограмме а – основание, h – высота. Какова площадь параллелограмма?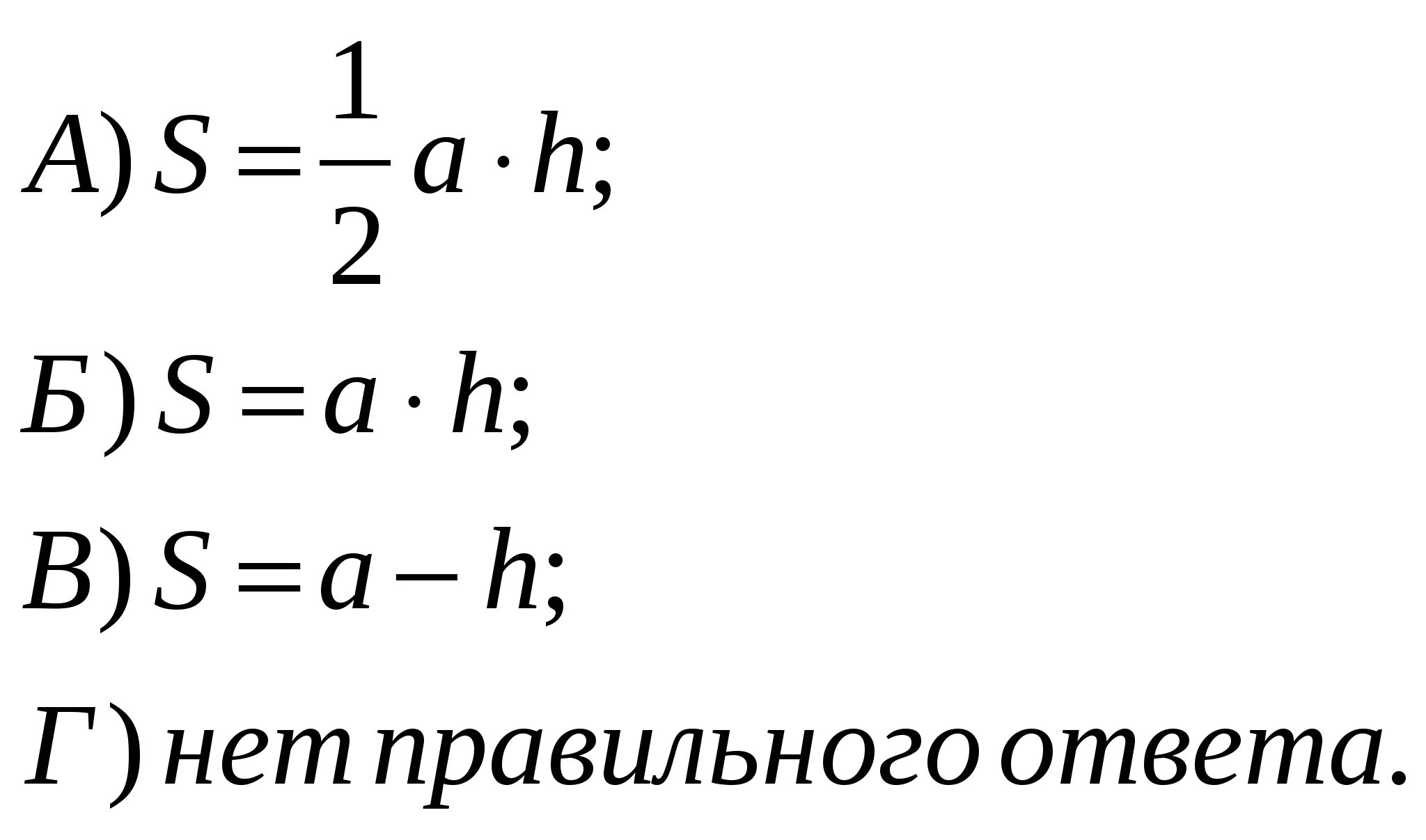
4	В прямоугольном треугольнике квадрат катета равен …	А) разности гипотенузы и катета; Б) разности квадратов гипотенузы и катета; В) сумме квадратов гипотенузы и катета; Г) нет правильного ответа.
5	Если вершина угла лежит на окружности, а стороны пересекают её, то это …	А) центральный угол; Б) развернутый угол; В) вписанный угол; Г) нет правильного ответа.
6	Треугольники подобны, если …	А) два угла одного тр-ка равны двум углам другого тр-ка; Б) две стороны одного тр-ка пропорциональны двум сторонам другого тр-ка; В) углы одного тр-ка пропорциональны углам другого тр-ка; Г) нет правильного ответа.
7	Средняя линия треугольника …	А) равна одной из сторон тр-ка; Б) делит одну сторону тр-ка пополам; В) параллельна одной из сторон тр-ка и равна ее половине; Г) нет правильного ответа.
8	Косинус острого угла прямоугольного треугольника – это отношение …	А) прилежащего катета к гипотенузе; Б) катетов; В) гипотенузы и катета; Г) нет правильного ответа.
9	Сумма острых углов прямоугольного треугольника равна …	А) 450; Б) 900; В) 1800; Г) нет правильного ответа.
10	Найдите стороны параллелограмма, если одна из них в 3 раза меньше другой, а периметр параллелограмма равен 60 см.
11	Найдите биссектрису угла, проведенную к основанию равнобедренного треугольника, если его боковая сторона равна 25 см, а основание равно 14 см.

№№	Вопросы	Варианты ответов
1	Параллелограмм – это четырехугольник, у которого …	А) все стороны равны; Б) противоположные стороны попарно параллельны; В) диагонали равны; Г) нет правильного ответа.
2	Квадрат – это прямоугольник, у которого …	А) диагонали перпендикулярны; Б) противоположные стороны равны; В) все стороны равны; Г) нет правильного ответа.
3	В трапеции основания а и в, высота – h. Какова площадь трапеции?	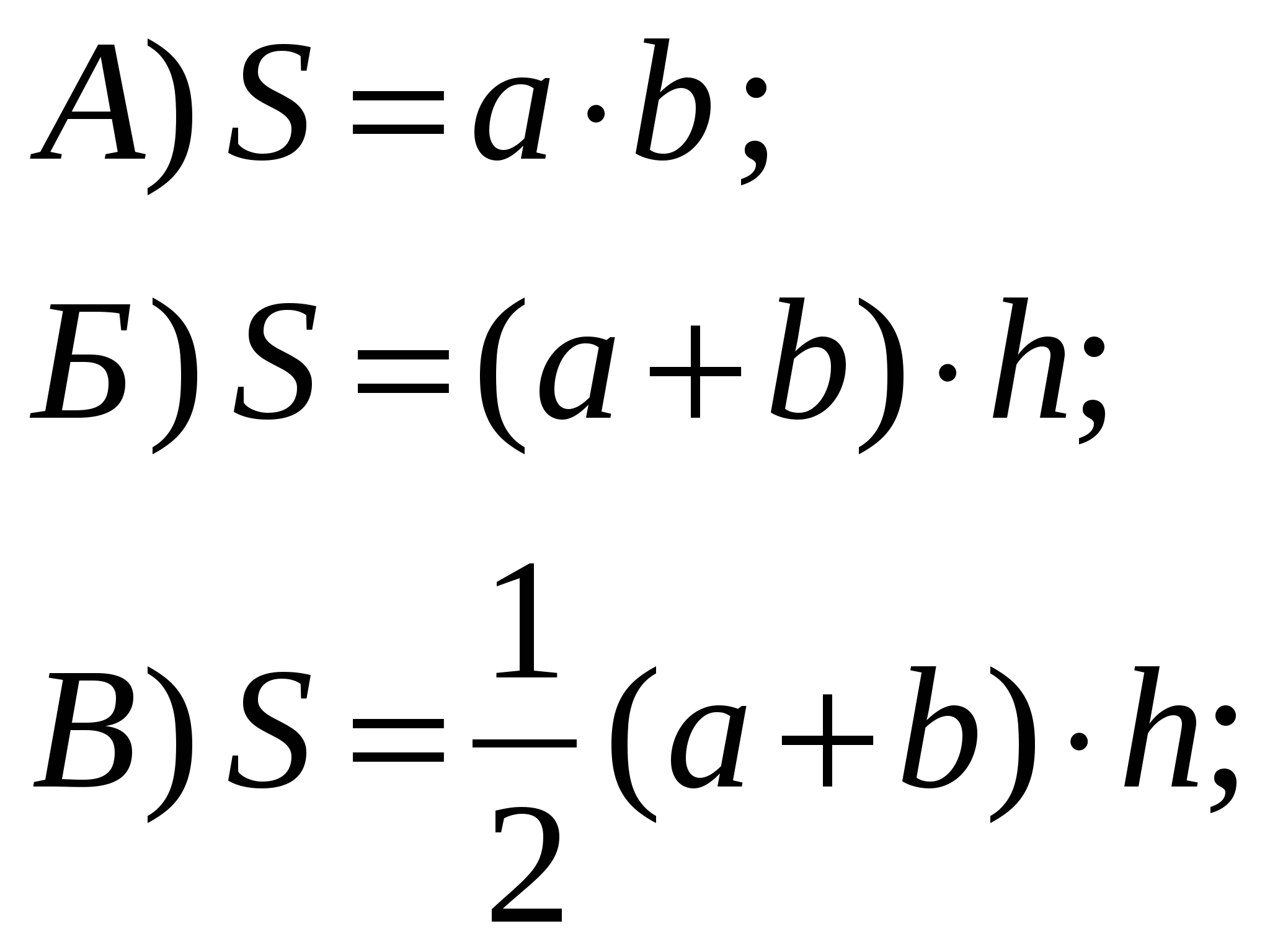Г) нет правильного ответа.
4	Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то этот треугольник …	А) прямоугольный; Б) равнобедренный; В) тупоугольный; Г) нет правильного ответа.
5	Центр вписанной в треугольник окружности – это точка пересечения …	А) высот; Б) медиан; В) биссектрис; Г) нет правильного ответа.
6	Треугольники подобны, если …	А) две стороны одного тр-ка пропорциональны сторонам другого; Б) две стороны одного тр-ка равны двум сторонам другого; В) два угла одного тр-ка равны двум углам другого; Г) нет правильного ответа.
7	Отношение площадей подобных треугольников равно …	А) коэффициенту подобия; Б) квадрату коэффициента подобия; В) cos 450; Г) нет правильного ответа.
8	Прямая, проходящая через конец радиуса, лежащий на окружности, и перпендикулярная к этому радиусу, является …	А) секущей; Б) касательной; В) диаметром; Г) нет правильного ответа.
9	Диагонали ромба …	А) равны; Б) перпендикулярны и точкой пересечения делятся пополам; В) параллельны; Г) нет правильного ответа.
10	Найдите стороны параллелограмма, если одна из них на 6 см больше другой, а периметр параллелограмма равен 42 см.
11	Найдите боковую сторону равнобедренного треугольника, если основание равно 10 см, а медиана, проведенная к основанию, равна 6 см.

№№	Вопросы	Варианты ответов
1	Ромб – это параллелограмм, у которого …	А) все стороны равны; Б) диагонали равны; В) углы равны; Г) нет правильного ответа.
2	Четырехугольник является параллелограммом, если …	А) все стороны равны; Б) диагонали точкой пересечения делятся пополам; В) диагонали равны; Г) нет правильного ответа.
3	В треугольнике сторона равна а, проведенная к ней высота – h. Площадь этого треугольника …	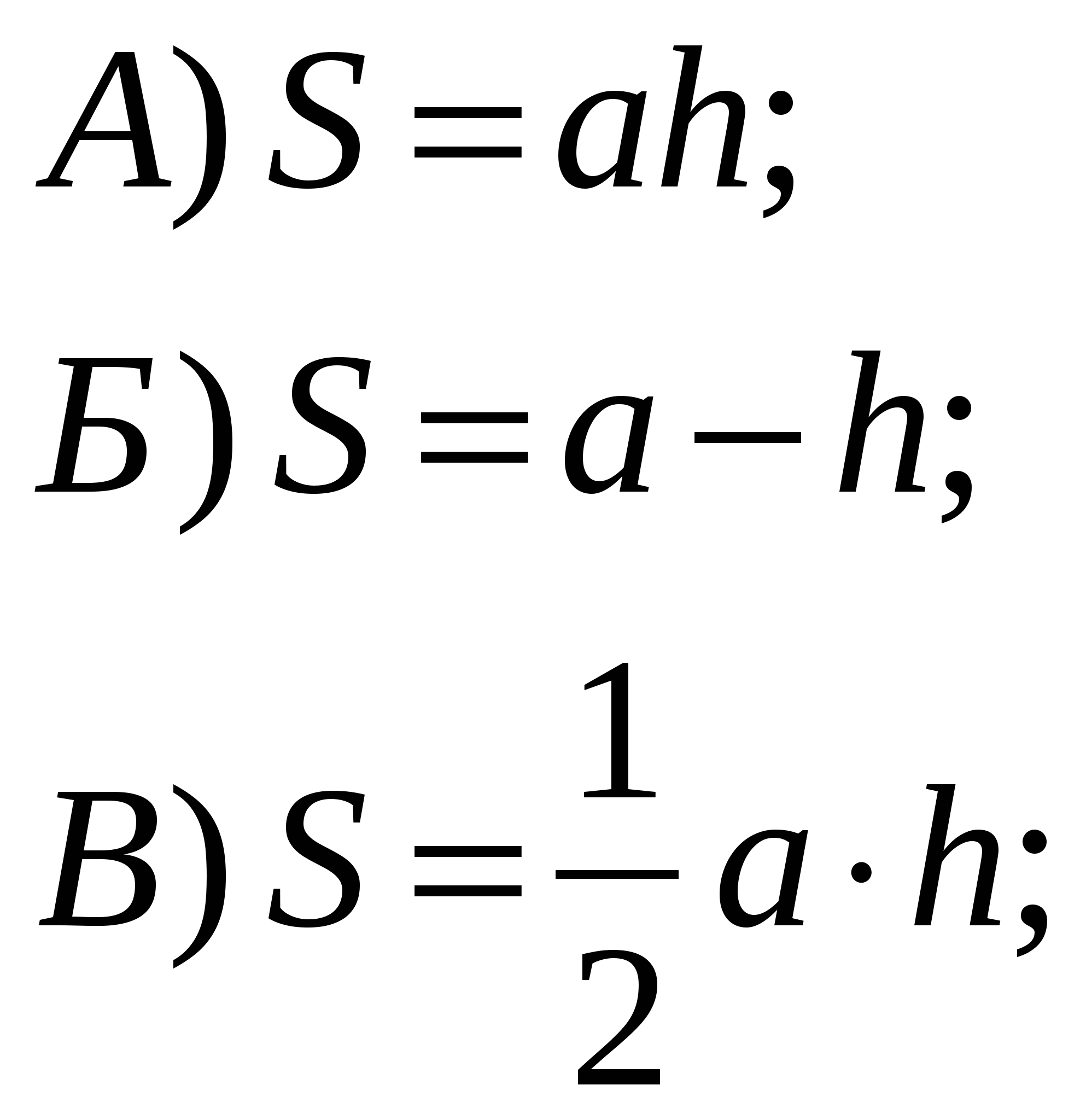Г) нет правильного ответа.
4	Квадрат гипотенузы равен сумме квадратов катетов в …	А) равностороннем треугольнике; Б) равнобедренном треугольнике; В) прямоугольном треугольнике; Г) нет правильного ответа.
5	Центр описанной около треугольника окружности – это точка пересечения …	А) серединных перпендикуляров к сторонам; Б) биссектрис; В) высот; Г) нет правильного ответа.
6	Треугольники подобны, если …	А) стороны одного тр-ка равны сторонам другого треугольника; Б) углы одного треугольника пропорциональны углам другого треугольника; В) две стороны одного тр-ка пропорциональны двум сторонам другого тр-ка; Г) нет правильного ответа.
7	Медианы треугольника точкой пересечения делятся в отношении ….., считая от вершины.	А) 2:1; Б) 3:5; В) 1:2; Г) нет правильного ответа.
8	Тангенс острого угла прямоугольного треугольника – это отношение …	А) противолежащего катета к гипотенузе; Б) гипотенузы к прилежащему катету; В) противолежащего катета к прилежащему; Г) нет правильного ответа.
9	Вписанный в окружность угол равен …	А) дуге, на которую он опирается; Б) половине дуги, на которую опирается; В) 1800; Г) нет правильного ответа.
10	Найдите стороны параллелограмма, если одна из них в 5 раз больше другой, а периметр параллелограмма равен 54 см.
11	Найдите основание равнобедренного треугольника, если его боковая сторона 15 см, а биссектриса угла, лежащего против основания, равна 12 см.

ПЕРЕЧЕНЬ КОНТРОЛЬНЫХ РАБОТ ПО ТЕМАМ

ПЕРЕЧЕНЬ ПРАКТИЧЕСКИХ РАБОТ

1. 
   Площадь квадрата, описанного около окружности, равна 16 см². Найдите площадь правильного треугольника, вписанного в ту же окружность.
   
2. 
   Две стороны треугольника равны 9 см и 21 см, а угол, противолежащий большей из них, – 60^о. Найдите периметр и площадь треугольника.
   
3. 
   В треугольнике АВС АВ=ВС=20 см, АС=24 см. Найдите:
   

1. 
   Площадь квадрата, вписанного в окружность, равна 16 см². Найдите площадь правильного треугольника, описанного около этой же окружности.
   
2. 
   Две стороны треугольника равны 33 см и 37 см, а угол, противолежащий большей из них, – 120^о. Найдите периметр и площадь треугольника.
   
3. 
   В треугольнике АВС АВ=ВС=15 см, АС=24 см. Найдите:
   

КОМПЛЕКТ ТЕОРЕТИЧЕСКИХ ВОПРОСОВ

НА КОНЕЦ ГОДА

1. 
   Что такое вектор? Какой вектор называется нулевым?
   
2. 
   Что называется длиной ненулевого вектора?
   
3. 
   Какие векторы называются коллинеарными?
   
4. 
   Дайте определение равных векторов.
   
5. 
   Какой вектор называется суммой двух векторов?
   
6. 
   В чем заключаются правило треугольника, правило параллелограмма и правило многоугольника для сложения векторов?
   
7. 
   Какой вектор называется разностью двух векторов?
   
8. 
   Какой вектор называется противоположным данному?
   
9. 
   Какой вектор называется произведением данного вектора на данное число?
   
10. 
    Сформулируйте основные свойства умножения вектора на число.
    
11. 
    Какой отрезок называется средней линией трапеции?
    
12. 
    Сформулируйте теорему о средней линии трапеции.
    
13. 
    Сформулируйте лемму о коллинеарных векторах.
    
14. 
    Сформулируйте теорему о разложении вектора по двум данным неколлинеарным векторам.
    
15. 
    Что такое координатные векторы?
    
16. 
    Что такое координаты вектора?
    
17. 
    Сформулируйте правила нахождения координат суммы и разности векторов, а также произведения вектора на число по заданным координатам векторов.
    
18. 
    Формулы для вычисления координат вектора по координатам его начала и конца.
    
19. 
    Формулы для вычисления координат середины отрезка по координатам его концов.
    
20. 
    Формула для вычисления расстояния между точками по их координатам.
    
21. 
    Какое уравнение называется уравнением данной линии. Напишите уравнение окружности данного радиуса с центром в данной точке.
    
22. 
    Напишите уравнение данной прямой в прямоугольной системе координат.
    
23. 
    Объясните, что такое синус и косинус угла α из промежутка 0⁰≤α≤180⁰.
    
24. 
    Что называется тангенсом угла α?
    
25. 
    Запишите основное тригонометрическое тождество.
    
26. 
    Напишите формулы приведения.
    
27. 
    Сформулируйте теорему синусов.
    
28. 
    Сформулируйте теорему косинусов.
    
29. 
    Объясните понятие угла между векторами.
    
30. 
    Какие два вектора называются перпендикулярными?
    
31. 
    Что такое скалярное произведение векторов?
    
32. 
    Напишите формулу, выражающую скалярное произведение векторов через их координаты.
    
33. 
    Сформулируйте свойства скалярного произведения векторов.
    
34. 
    Какой многоугольник называется правильным?
    
35. 
    Напишите формулу для вычисления угла правильного п-угольника.
    
36. 
    Сформулируйте теорему об окружности, описанной около правильного многоугольника.
    
37. 
    Сформулируйте теорему об окружности, вписанной в правильный многоугольник.
    
38. 
    Напишите формулу для вычисления площади правильного многоугольника через его периметр и радиус вписанной окружности.
    
39. 
    Напишите формулы для вычисления стороны правильного п-угольника и радиуса вписанной в него окружности через радиус описанной окружности.
    
40. 
    Напишите формулы для вычисления длины окружности и длины дуги окружности.
    
41. 
    Напишите формулы для вычисления площади круга и площади кругового сектора.
    
42. 
    Объясните, что такое отображение плоскости на себя.
    
43. 
    Какое отображение плоскости называется осевой симметрией, центральной симметрией?
    
44. 
    Что такое движение плоскости?
    
45. 
    Какое отображение плоскости называется параллельным переносом?
    
46. 
    Какое отображение плоскости называется поворотом?
    
47. 
    Объясните, что такое многогранник и назовите его элементы.
    
48. 
    Объясните, как построить призму, и назовите ее элементы.
    
49. 
    Какая призма называется: а) прямой; б) правильной?
    
50. 
    Объясните, как измеряются объемы тел и перечислите основные свойства объемов.
    
51. 
    Свойство диагонали прямоугольного параллелепипеда.
    
52. 
    Формула объем прямоугольного параллелепипеда.
    
53. 
    Какой многогранник называется пирамидой? Назвать и показать ее элементы.
    
54. 
    Какое тело называется цилиндром? Назовите и покажите его элементы.
    
55. 
    Формулы объема цилиндра и площади его боковой поверхности.
    
56. 
    Объясните, какое тело называется конусом. Назовите и покажите элементы конуса.
    
57. 
    Формулы объема и площади боковой поверхности конуса.
    
58. 
    Что называется сферой и что такое ее центр, радиус и диаметр?
    
59. 
    Какое тело называется шаром, и что такое его центр, радиус и диаметр?
    
60. 
    Формулы объема шара и площади сферы.