Главная страница
Анализ
Анкета
архив
Биография
Бюллетень
Викторина
Глава
Диплом
Доклад
Документация
Задача

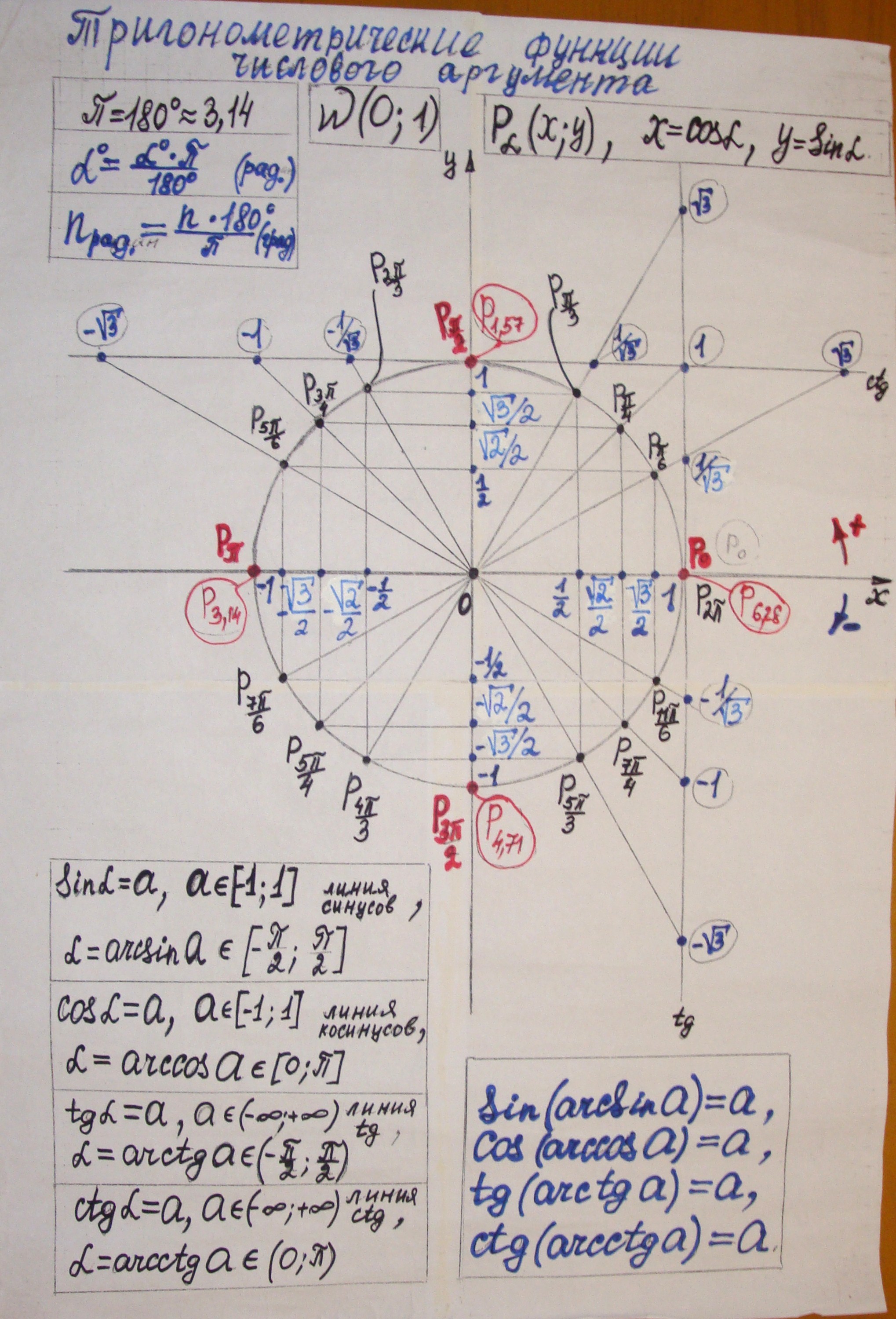
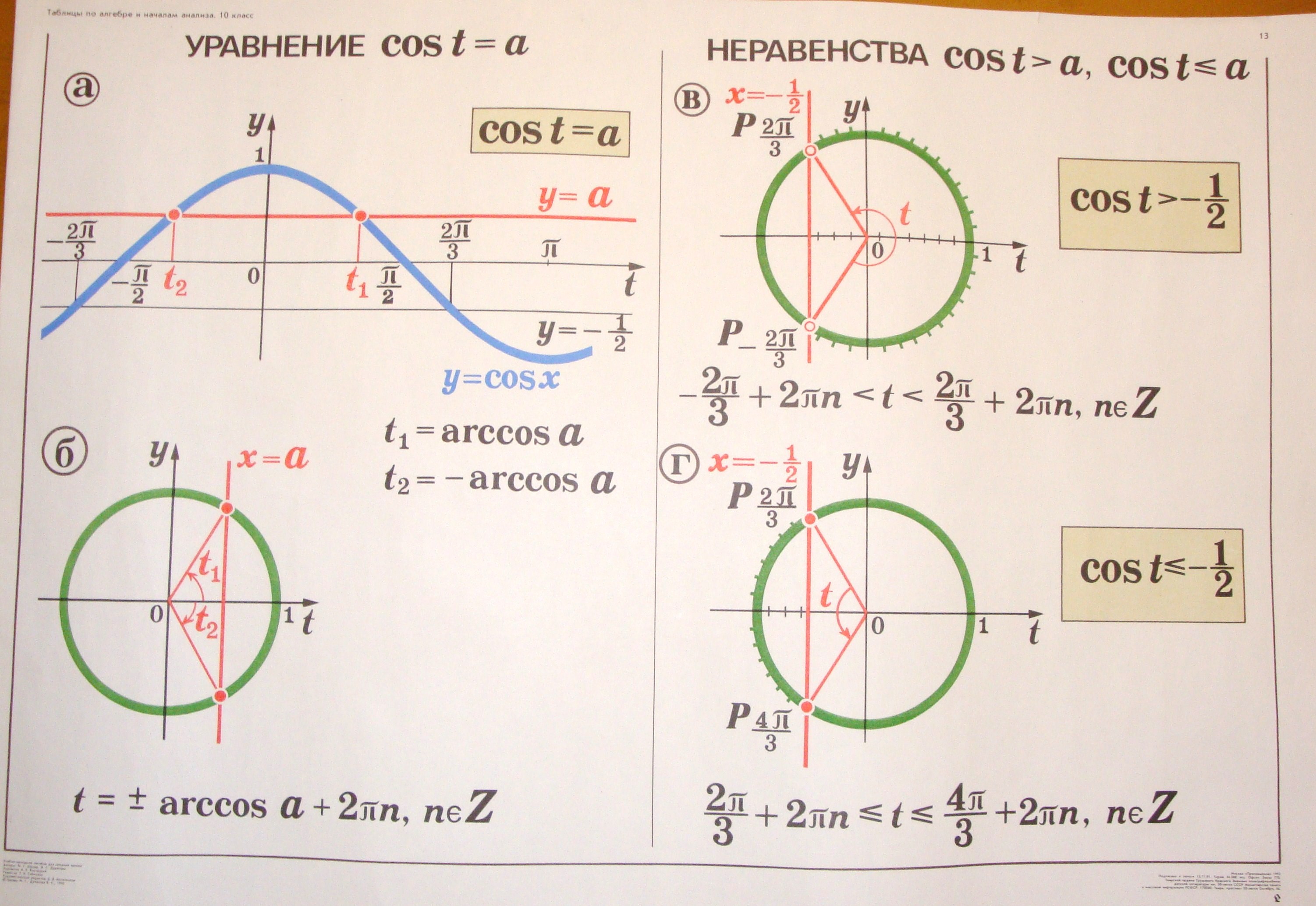
Урока Тема урока: «Арккосинус и решение уравнения cos t = a». Учебный предмет: алгебра и начала анализа. Класс: 10 класс



Скачать 94.25 Kb.
НазваниеУрока Тема урока: «Арккосинус и решение уравнения cos t = a». Учебный предмет: алгебра и начала анализа. Класс: 10 класс
Дата13.02.2016
Размер94.25 Kb.
ТипУрок

Технологическая карта дистанционного урока

Тема урока: «Арккосинус и решение уравнения cos t = a».

Учебный предмет: алгебра и начала анализа.

Класс: 10 класс.

Тип урока: поисковая беседа.

Ученик: Елизавета.

Цели урока:

Обучающая: организовать работу по усвоению новых понятий (научить решать простейшие тригонометрические уравнения вида cos t = a, используя, числовую окружность и по формулам, вычислять значения обратных тригонометрических функций; осуществлять отбор корней в простейших уравнениях вида cos t = a).

Развивающая: упражнять в самостоятельном анализе, сравнении, умозаключениях.

Воспитательная: воспитывать трудолюбие, ответственность и самостоятельность в принятии решений.

Основная проблема занятия: как записать на математическом языке решение уравнения cos t = 2/5 вывести общую формулу для решения уравнения cos t = a.

Проблема, поставленная в перспективу (над ней ученики смогут подумать после занятий): вывести общую формулу для решения уравнения sin t = a .

Учащиеся создают на уроке: новые знания (arccos a (его состав), определение арккосинуса в общем виде, общая формула решения уравнения вида cos t = a, частные случаи cos t = 0, cos t = 1, cos t = -1 ).

Учащиеся учатся на уроке: формулировать проблему; устанавливать связи между новыми и уже имеющимися знаниями; решение проблемы - награда за труды.

Краткий план занятия:

1) актуализация знаний;

2) создание проблемной ситуации;

3) выдвижение гипотезы;

4) поиск решения проблемы;

5) проверка найденного решения.

Этапы урока:

1)орг. момент (2 мин.);

2) актуализация знаний (5 мин.);

3) создание проблемной ситуации (5 мин.);

4) физ. минутка (2 мин.);

5) выдвижение гипотезы (5 мин.);

6) поиск решения проблемы (15мин.);

7) проверка найденного решения (6 мин.);

8) итоги урока: дом. задание, оценка за урок, постановка проблемы на следующий урок. (5 мин.).

Учитель организует работу ученика по созданию проблемной ситуации, если она не возникла на этапе актуализации. После постановки проблемы, организует поиск её решения и проверку на практике правильности решения учебной проблемы.

После урока анализирует результаты урока, планирует работу на следующий урок.

О рефлексии и результативности занятия можно будет судить по результатам опроса.

Технические средства обучения и оборудование. специализированный программно-технический комплекс ученика с ограниченными возможностями здоровья:

компьютер Apple Mac mini, Мышь Logitech RX250, Клавиатура Apple Keyboard, Монитор LG W2043T, Системное программное обеспечение Apple Mac OS X Snow Leopard, Наушники DIALOG M-881HV, Микрофон USB Desktop Microphone, Колонки Dialog W-203, Веб-камера CNR-WCAM820; компьютерные программы — Skype, УМК «Живая математика», презентация Power Point, электронные файлы (Word 2007):»; учебник «Алгебра и начала математического анализа» базовый уровень. Изд. «Мнемозина» под ред. Мордкович А.Г.. Москва.

План урока.

Деятельность учителя.
Деятельность ученика.

1)орг. момент (2 мин.);



-приветствие ученика;

-перед уроком учитель загружает УМК «Живая математика»;

-включает демонстрацию экрана;

-сообщение темы урока: «Арккосинус и решение уравнения cos t = a».

Перед изучением новой темы необходимо повторить материал, изученный ранее.
-приветствие учителя;

-перед уроком ученик загружает УМК «Живая математика».

  1. актуализация знаний

    (5 мин.);




Сдать дом. практическую работу ( Презентация «Преобразование графиков тригонометрических функций»).

Определите координаты точек, значения cos t и Sin t :

Р п/3

Р п/2

Р п

Р п/4

Р- п/3

Р -п/2

Р -п

Р- п/4

Используя числовую окружность,найти значение t:

cos t = 0, t= +п/2; - п/2
cos t = ½ t= +п/3; - п/3
cos t = 3, t=
cos t = - ¾, t=
cos t = -1, t=+ п ; - п
cos t = √3/2, t=+п/6; - п/6
cos t = ¾, t=
cos t = -√3/2, t=+5п/6; - 5п/6
cos t = −½, t=+2п/3; - 2п/3
cos t = 2/5.
cos t = - √2/2, t= +3 п/4: -3 п/4
cos t = 1, t=0
cos t = −5, t=
cos t = √2/2, t=+п/4; - п/4
cos t = - 2/5.




Отвечает на поставленный вопрос, если возникают трудности, то повторяем числовую окружность, где находятся значения тригонометрических функций на числовой окружности, их периодичность.

Не забываем + 2Пк, где к-целое .

Найти ошибки в записи.

3) создание проблемной ситуации (5 мин.);




1) Что это за число t,

при котором cos t = 2/5, cos t = -2/5, cos t = ¾ , cos t = - ¾ ?

2) Как же решается уравнение вида cos t = а?



4) физ. минутка (2 мин.);




5) выдвижение гипотезы (5 мин.);



Разрешимо ли это уравнение?

Ведь на линии косинусов есть значение 2/5, значит и решение уравнения существует, как записать его?

Ввожу новое понятие.

Арккосинус двух пятых (arcus в переводе с латинского значит дуга-арка)
Длина дуги числовой окружности равна arccos 2/5 .

arccos 2/5

(arc)-математический знак,

cos t - исходная функция,

2/5 напоминание о правой части уравнения cos t = 2/5
+ arccos 2/5

- arccos 2/5

Определение:

если│а│≤ 1, то

arccos a = t ↔ { cos t = a, 0 ≤ t ≤ П.

arccos a - это такое число из отрезка [0;П], косинус которого равен а.






  1. поиск решения проблемы (15мин.);



Решить уравнение:

cos t = 2/5,


cos t = - 2/5,


cos t = 3,
cos t = −5,
cos t = 1,
cos t = -1,
cos t =0.
cos t = a,

Все ли корни уравнения указаны?

Будет ли корнем уравнения корень

arccos( 0,5) + 2п;
arccos( 0,5) + 22п;
arccos( 0,5) — 12п;

cos t = 2/5.

t =+-arccos 2/5 + 2Пк, где к-целое.

cos t = - 2/5.

t =+-arccos( -2/5) + 2Пк, где к-целое.
Решений нет.
Решений нет.
t = 2Пк, где к-целое.
t = П + 2Пк, где к-целое .
t = П/2 + 2Пк, где к-целое .
t =+-arccos a + 2Пк, где к-целое.

Проблема решена!!!!









7) проверка найденного решения (6 мин.);




Решить уравнения:
cos t = - ¾,
cos t = ¾.

Найти значение выражения:
arccos 0,5,
arccos 5/2,

arccos 0
cos t = ¾,
arccos (-1)




8) итоги урока: дом. Задание глава3,§15,№15.1 - №15.7(в,г); оценка за презентацию (хорошо), оценка за урок (отлично), постановка проблемы на следующий урок. (5 мин.).




Проблема, поставленная в перспективу: Как же решается уравнение вида sin t = а?

Ученик подводит итог урока, отвечая на вопросы; 1) решены ли проблемы, поставленные в начале урока; 2) какие новые знания открыл для себя на уроке; 3) применение новых знаний при решении задач.

Рефлексия: ученик заинтересовался поставленной перед ним проблемой – всё прекрасно, знания будут; не заинтересовался – заинтересуем на следующем уроке.