Рабочая программа по алгебре разработана на основании авторской программы по математике для 5-6 классов (автор В. И. Жохов,М.: Мнемозина,2009) и учебного плана мбоу сш №5 г. Павлово
 Скачать 392.94 Kb. Скачать 392.94 Kb.
|
1 2
| Пояснительная записка Рабочая программа по алгебре разработана на основании авторской программы по математике для 5-6 классов (автор В.И.Жохов,М.:Мнемозина,2009) и учебного плана МБОУ СШ №5 г.Павлово. Рабочая программа составлена для учащихся 6 класса МБОУ СШ №5, рассчитана на 175 часов в год, 5 часа в неделю. В основу изучения курса положены принципы: дидактические (научности, сознательности и активности, наглядности, систематичности и последовательности, прочности, доступности, связи обучения с жизнью); воспитания (социальной активности, социального творчества, развивающее воспитание, мотивированность, проблемность, индивидуализация, опора на ведущую деятельность); развития (деятельности, непрерывности, целостного представления о мире, минимакса, психологической комфортности, вариативности, творчества); педагогики здоровья: ненанесения вреда; субъект-субъектного взаимоотношения с учащимися; соответствия содержания и организации обучения возрастным особенностям учащихся; гармоничного сочетания обучающих, воспитывающих и развивающих педагогических воздействий; приоритет активных методов обучения; принцип отсроченного результата Цели и задачи изучения курса математики: Развитие:
Формированиепредставлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов Воспитание:
Общая характеристика учебного предмета: Курс математики 6-го класса – важное звено математического образования и развития школьников. На этом этапе заканчивается изучение вопросов, связанных с натуральными числами и завершается работа над формированием навыков арифметических действий с обыкновенными дробями. Формируются понятия «общий делитель» и «общее кратное», необходимые для полного усвоения основного свойства дроби. Даются первые знания о положительных и отрицательных числах, вводятся арифметические действия над положительными и отрицательными числами, что позволяет ознакомить учащихся с общими приемами решения линейных уравнений с одним неизвестным. Особое внимание уделяется усвоению понятия модуля числа. Продолжается обучение решению текстовых задач, совершенствуются и обогащаются умения геометрических построений и измерений. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. При этом учащиеся постепенно осознают правила выполнения основных логических операций. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов. Используются педагогические технологии: методы дифференцированного и здоровьесберегающего обучения, личностно-ориентированное обучение. Методы :
Формы текущего и итогового контроля: контроль осуществляется в виде самостоятельных работ, математических диктантов, тестов, контрольных работ. Календарно-тематическое планирование Математика, 6 класс, 5 часа в неделю (175ч в год)
Содержание тем учебного курса 1. Делимость чисел Делители и кратные числа. Общий делитель и общее кратное. Признаки делимости на 2, 3, 5, 9, 10. Простые и составные числа. Разложение натурального числа на простые множители. Основная цель — завершить изучение натуральных чисел, подготовить основу для освоения действий с обыкновенными дробями. В данной теме завершается изучение вопросов, связанных с натуральными числами. Основное внимание должно быть уделено знакомству с понятиями «делитель» и «кратное», которые находят применение при сокращении обыкновенных дробей и при их приведении к общему знаменателю. Упражнения полезно выполнять с опорой на таблицу умножения — прямым подбором. Определенное внимание уделяется знакомству с признаками делимости, понятиям простого и составного чисел. При их изучении целесообразно формировать умения проводить простейшие умозаключения, обосновывая свои действия ссылками на определение, правило. Учащиеся должны уметь разложить число на множители. Например, они должны понимать, что 36 = 6· 6 = 4· 9 = 2 ·18 и т. п. Умения разложить число на простые множители не обязательно добиваться от всех учащихся. 2. Сложение и вычитание дробей с разными знаменателями Основное свойство дроби. Сокращение дробей. Приведение дробей к общему знаменателю. Понятие о наименьшем общем знаменателе нескольких дробей. Сравнение дробей. Сложение и вычитание дробей. Решение текстовых задач. Основная цель — выработать прочные навыки преобразования дробей, сложения и вычитания дробей. Одним из важнейших результатов обучения является усвоение основного свойства дроби, применяемого для преобразования дробей: сокращения, приведения к новому знаменателю. Умение приводить дроби к общему знаменателю используется для сравнения дробей. При рассмотрении действий с дробями используются правила сложения и вычитания дробей с одинаковыми знаменателями, понятие смешанного числа. Важно обратить внимание на случай вычитания дроби из целого числа. 3. Умножение и деление обыкновенных дробей Умножение и деление обыкновенных дробей. Основные задачи на дроби. Основная цель — выработать прочные навыки арифметических действий с обыкновенными дробями и решения основных задач на дроби. В этой теме завершается работа над формированием навыков арифметических действий с обыкновенными дробями. Навыки должны быть достаточно прочными, чтобы учащиеся не испытывали затруднений в вычислениях с рациональными числами, чтобы алгоритмы действий с обыкновенными дробями могли стать в дальнейшем опорой для формирования умений выполнять действия с алгебраическими дробями. Расширение аппарата действий с дробями позволяет решать текстовые задачи, в которых требуется найти дробь от числа или число по данному значению его дроби. 4. Отношения и пропорции Пропорция. Основное свойство пропорции. Решение задач с помощью пропорции. Понятия о прямой и обратной пропорциональности величин. Задачи на пропорции. Масштаб. Формулы длины окружности и площади круга. Шар. Основная цель — сформировать понятия пропорции, прямой и обратной пропорциональности величин. Необходимо, чтобы учащиеся усвоили основное свойство пропорции, так как оно находит применение на уроках математики, химии, физики. В частности, достаточное внимание должно быть уделено решению с помощью пропорции задач на проценты. Понятия о прямой и обратной пропорциональности величин можно сформировать как обобщение нескольких конкретных примеров, подчеркнув при этом практическую значимость этих понятий, возможность их применения для упрощения решения соответствующих задач. В данной теме даются представления о длине окружности и площади круга. Соответствующие формулы к обязательному материалу не относятся. Рассмотрение геометрических фигур завершается знакомством с шаром. 5. Положительные и отрицательные числа Положительные и отрицательные числа. Противоположные числа. Модуль числа и его геометрический смысл. Сравнение чисел. Целые числа. Изображение чисел на координатной прямой. Координата точки. Основная цель — расширить представления учащихся о числе путем введения отрицательных чисел. Целесообразность введения отрицательных чисел показывается на содержательных примерах. Учащиеся должны научиться изображать положительные и отрицательные числа на координатной прямой. В дальнейшем она будет служить наглядной основой для правил сравнения чисел, сложения и вычитания чисел. Специальное внимание должно быть уделено усвоению вводимого здесь понятия модуля числа, прочное знание которого необходимо для формирования умения сравнивать отрицательные числа, а в дальнейшем и для овладения алгоритмами арифметических действий с положительными и отрицательными числами. 6. Сложение и вычитание положительных и отрицательных чисел Сложение и вычитание положительных и отрицательных чисел. Основная цель — выработать прочные навыки сложения и вычитания положительных и отрицательных чисел. Действия с отрицательными числами вводятся на основе представлений об изменении величин: сложение и вычитание чисел иллюстрируется соответствующими перемещениями точек координатной прямой. При изучении данной темы отрабатываются алгоритмы сложения и вычитания при выполнении действий с целыми и дробными числами. 7. Умножение и деление положительных и отрицательных чисел Умножение и деление положительных и отрицательных чисел. Понятие о рациональном числе, десятичное приближение обыкновенной дроби. Применение законов арифметических действий для рационализации вычислений. Основная цель — выработать прочные навыки арифметических действий с положительными и отрицательными числами. Навыки умножения и деления положительных и отрицательных чисел отрабатываются сначала при выполнении отдельных действий, а затем в сочетании с навыками сложения и вычитания при вычислении значений числовых выражений. При изучении данной темы учащиеся должны усвоить, что для обращения обыкновенной дроби в десятичную достаточно разделить (если это возможно) числитель на знаменатель. В каждом конкретном случае они должны знать, в какую дробь обращается данная обыкновенная дробь — в десятичную или периодическую. Учащиеся должны знать представление в виде десятичной дроби таких дробей, как 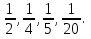 8. Решение уравнений Простейшие преобразования выражений: раскрытие скобок, приведение подобных слагаемых. Решение линейных уравнений. Примеры решения текстовых задач с помощью линейных уравнений. Основная цель — подготовить учащихся к выполнению преобразований выражений, решению уравнений. Преобразования буквенных выражений путем раскрытия скобок и приведения подобных слагаемых отрабатываются в той степени, в которой они необходимы для решения несложных уравнений. Введение арифметических действий над отрицательными числами позволяет ознакомить учащихся с общими приемами решения линейных уравнений с одной переменной. 9. Координаты на плоскости Построение перпендикуляра к прямой и параллельных прямых с помощью чертежного треугольника и линейки. Прямоугольная система координат на плоскости, абсцисса и ордината точки. Примеры графиков, диаграмм. Основная цель — познакомить учащихся с прямоугольной системой координат на плоскости. Учащиеся должны научиться распознавать и изображать перпендикулярные и параллельные прямые. Основное внимание следует уделить отработке навыков их построения с помощью линейки и чертежного треугольника, не требуя воспроизведения точных определений. Основным результатом знакомства учащихся с координатной плоскостью должны стать знания порядка записи координат точек плоскости и их названий, умения построить координатные оси, отметить точку по заданным координатам, определить координаты точки, отмеченной на координатной плоскости. Формированию вычислительных и графических умений способствует построение столбчатых диаграмм. При выполнении соответствующих упражнений найдут применение изученные ранее сведения о масштабе и округлении чисел. 10. Повторение. Решение задач Основные требования к уровню подготовки обучающихся Делимость чисел Учащиеся должны знать/понимать:
Учащиеся должны уметь:
Сложение и вычитание дробей с разными знаменателями Учащиеся должны знать/понимать:
Учащиеся должны уметь:
Умножение и деление обыкновенных дробей. Учащиеся должны знать/понимать:
Учащиеся должны уметь:
Отношения и пропорции Учащиеся должны знать/понимать:
Учащиеся должны уметь:
Положительные и отрицательные числа Учащиеся должны знать/понимать:
Учащиеся должны уметь:
Сложение и вычитание положительных и отрицательных чисел Учащиеся должны знать/понимать:
Учащиеся должны уметь:
Умножение и деление положительных и отрицательных чисел Учащиеся должны знать/понимать:
Учащиеся должны уметь:
Решение уравнений Учащиеся должны знать/понимать:
Учащиеся должны уметь:
Координаты на плоскости Учащиеся должны знать/понимать:
Учащиеся должны уметь:
Контрольно-измерительные материал Контрольная работа №1 Вариант I 1.Найдите: а) наибольший общий делитель чисел 24 и 18 б) наименьшее общее кратное чисел 12 и 15 2. Разложите на простые множители число 546. 3. Какую цифру можно записать вместо звездочки в числе 681*, чтобы оно а) делилось на 9 б) делилось на 5 в) было кратно 6 4.Выполните действия а) 7 – 2,35 + 0,435 б) 1,763:0,086 – 0,34∙16 5. Найдите произведение чисел a и b, если их наименьшее общее кратное равно 420, а наибольший общий делитель равен 30. Вариант II 1. Найдите а) наибольший общий делитель чисел 28 и 42 б) наименьшее общее кратное чисел 20 и 35 2. Разложите на простые множители число 510. 3. Какую цифру можно записать вместо звездочки в числе 497*, чтобы оно а) делилось на 3 б) делилось на 10 в) было кратно 9 4. Выполните действия а) 9 – 3,46 +0,535 б) 2,867:0,094 + 0,31∙15 5. Найдите наименьшее общее кратное чисел m и n, если их произведение равно 67200, а наибольший общий делитель равен 40. Контрольная работа №2 Вариант I 1. Сократите: 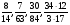 2. Выполните действия а) 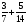 б) б) 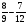 в) в) 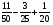 3. Решите уравнение а) 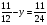 б) 5,86х + 1,4х = 76,23 б) 5,86х + 1,4х = 76,234. В первые сутки теплоход прошёл 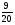 всего пути, во вторые сутки – на всего пути, во вторые сутки – на 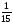 пути больше, чем в первые. Какую часть всего пути теплоход прошел за эти двое суток? пути больше, чем в первые. Какую часть всего пути теплоход прошел за эти двое суток?5. Найдите четыре дроби, каждая из которых больше 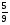 и меньше и меньше 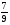 . .Вариант II 1. Сократите: 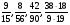 2. Выполните действия а) 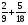 б) б) 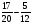 в) в) 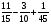 3. Решите уравнение а) 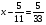 б) 6,28х – 2,8х = 36,54 б) 6,28х – 2,8х = 36,544. В первый день засеяли 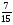 всего поля, во второй день засеяли на всего поля, во второй день засеяли на 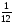 поля меньше, чем в первый. Какую часть поля засеяли за эти два дня? поля меньше, чем в первый. Какую часть поля засеяли за эти два дня?5. Найдите четыре дроби, каждая из которых больше 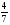 и меньше и меньше 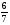 . .Контрольная работа №3 Вариант I 1. Сравните числа а) 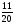 и и 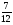 б) б) 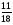 и и 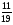 в) 0,48 и в) 0,48 и 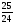 2. Найдите значение выражения а) 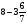 б) б) 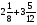 в) в) 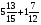 г) г) 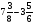 3. На автомашине планировали перевезти сначала 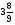 т груза, а потом ещё т груза, а потом ещё 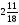 т. Однако перевезли на т. Однако перевезли на 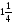 т меньше, чем предполагали. Сколько всего тонн груза перевезли на автомашине? т меньше, чем предполагали. Сколько всего тонн груза перевезли на автомашине?4. Решите уравнение а) 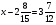 б) 3,45∙(2,08 – к) = 6,21 б) 3,45∙(2,08 – к) = 6,215. Представьте дробь 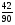 в виде суммы трех дробей, у каждой из которых числитель равен 1. в виде суммы трех дробей, у каждой из которых числитель равен 1.Вариант II 1. Сравните числа а) 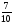 и и 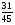 б) б) 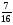 и и 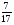 в) в) 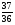 и 0,72 и 0,722. Найдите значения выражения а)7 - 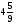 б) б) 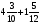 в) в) 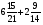 г) г) 3. С одного опытного участка рассчитывали собрать 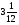 т пшеницы, а с другого т пшеницы, а с другого 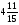 т. Однако с них собрали на т. Однако с них собрали на 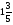 т пшеницы больше. Сколько тонн пшеницы собрали с этих двух участков? т пшеницы больше. Сколько тонн пшеницы собрали с этих двух участков?4. Решите уравнение а) 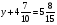 б) 2,65∙(к – 3,06) = 4,24 б) 2,65∙(к – 3,06) = 4,245. Представьте дробь 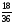 в виде суммы трех дробей, у каждой из которых числитель равен 1. в виде суммы трех дробей, у каждой из которых числитель равен 1.Контрольная работа №4 Вариант I 1. Найдите произведение а) 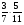 б) б) 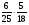 в) в)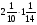 г) г)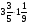 д) д) 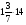 2. Выполните действия а) 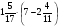 б) (4,2:1,2 – 1,05)∙1,6 б) (4,2:1,2 – 1,05)∙1,63. В один пакет насыпали 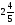 кг пшена, а в другой кг пшена, а в другой 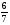 этого количества. На сколько меньше пшена насыпали во второй пакет чем в первый? этого количества. На сколько меньше пшена насыпали во второй пакет чем в первый?4. Упростите выражение 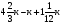 и найдите его значение при к = и найдите его значение при к = 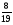 . .5. В овощехранилище привезли 320т овощей. 75% привезенных овощей составлял картофель, а 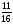 остатка – капуста. Сколько тонн капусты привезли в овощехранилище? остатка – капуста. Сколько тонн капусты привезли в овощехранилище?Вариант II 1. Найдите произведение а) 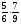 б) б) 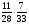 в) в) 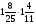 г) г) 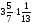 д) д) 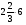 2. Выполните действия а) 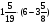 б) (6,3:1,4 – 2,05)∙1,8 б) (6,3:1,4 – 2,05)∙1,83. Площадь одного участка земли 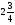 га, а другого – в га, а другого – в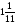 раза больше. На сколько гектаров площадь первого участка меньше площади второго? раза больше. На сколько гектаров площадь первого участка меньше площади второго?4. Упростите выражение 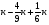 и найдите его значение при к = и найдите его значение при к =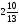 . .5. В книге 240 страниц. Повесть занимает 60% книги, а рассказы 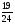 остатка. Сколько страниц в книге занимают рассказы? остатка. Сколько страниц в книге занимают рассказы?Контрольная работа №5 Вариант I 1. Выполните действия а) 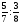 б) б) 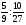 в) в) 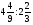 г) г) 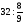 д) д) 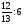 2. За 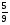 кг конфет заплатили 15р. Сколько стоит 1кг этих конфет? кг конфет заплатили 15р. Сколько стоит 1кг этих конфет?3. Решите уравнение а) 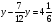 б) (3,1х + х):0,8 = 2,05 б) (3,1х + х):0,8 = 2,054. У Сережи и Пети всего 69 марок. У Пети марок в 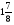 раза больше, чем у Сережи. Сколько марок у каждого из мальчиков? раза больше, чем у Сережи. Сколько марок у каждого из мальчиков?5. Сравните числа р и к, если 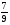 числа р равны 35% числа к. числа р равны 35% числа к.Вариант II 1. Выполните действия а) 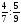 б) б) 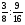 в) в) 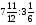 г) г) 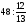 д) д) 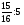 2. За 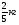 печенья заплатили 6р. Сколько стоит 1кг этого печенья? печенья заплатили 6р. Сколько стоит 1кг этого печенья?3. Решите уравнение: а) 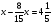 б) (7,1у – у):0,6 = 3,05 б) (7,1у – у):0,6 = 3,054. В два железнодорожных вагона погрузили 91 т угля. Во втором вагоне угля оказалось в 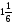 раза больше. Сколько угля погрузили в каждый из этих вагонов? раза больше. Сколько угля погрузили в каждый из этих вагонов?5. Сравните числа р и к, если 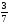 числа р равны 15% числа к. числа р равны 15% числа к.Контрольная работа №6 Вариант I 1. Найдите значение выражения: а) 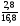 б) б) 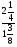 в) в) 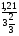 2. Решите уравнение 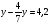 3. Вспахали 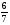 поля, что составило 210 га. Какова площадь всего поля? поля, что составило 210 га. Какова площадь всего поля?4. Заасфальтировали 35% дороги, после чего осталось заасфальтировать ещё 13 км. Какова длина всей дороги? 5. 0,9 от 20% числа р равны 5,49. Найдите число р. Вариант II 1. Найдите значение выражения: а) 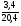 б) б) 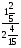 в) в) 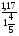 2. Решите уравнение 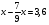 3. Заасфальтировали 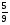 дороги, что составило 45 км. Какова длина всей дороги? дороги, что составило 45 км. Какова длина всей дороги?4. Вспахали 45% поля, после чего осталось вспахать ещё 165 га. Какова площадь всего поля? 5. 0,7 от 40% числа d равны 2,94. Найдите число d. Контрольная работа №7 Вариант I 1. Решите уравнение 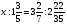 2. Автомобиль первую часть пути прошёл за 2,8 ч, а вторую – за 1,2ч. Во сколько раз меньше времени израсходовано на вторую часть пути, чем на первую? Сколько процентов всего времени движения затрачено на первую часть пути? 3. В 8 кг картофеля содержится 1,4 кг крахмала. Сколько крахмала содержится в 28 кг картофеля? 4. Поезд путь от одной станции до другой прошёл за 3,5 ч со скоростью 70 км/ч. С какой скоростью должен был идти поезд, чтобы пройти этот путь за 4,9ч? 5. 40% от 30% числа х равны 7,8 Найдите число х. Вариант II 1. Решите уравнение 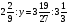 2. Трубу разрезали на две части длиной 3,6м и 4,4м. Во сколько раз первая труба короче второй? Сколько процентов длины всей трубы составляет длина первой её части? 3. Из 6 кг льняного семени получается 2,7 кг масла. Сколько масла получится из 34 кг семян льна? 4. Теплоход прошел расстояние между двумя пристанями со скоростью 40 км/ч за 4,5ч. С какой скоростью должен идти теплоход, чтобы пройти это расстояние за 3,6ч? 5. 60% от 40% числа у равны 8,4. Найдите число у. Контрольная работа №8 Вариант I 1. Найдите длину окружности, если её диаметр равен 25 см. Число п округлите до десятых. 2. Расстояние между двумя пунктами на карте равно 3,8 см. Определите расстояние между этими пунктами на местности, если масштаб карты 1:100000. 3. Найдите площадь круга, радиус которого равен 6 м. Число п округлите до десятых. 4. Цена товара понизилась с 42,5р. до 37,4р. На сколько процентов понизилась цена товара? 5. Прямоугольный земельный участок изображен на плане в масштабе 1:300. Какова площадь земельного участка, если площадь его изображения на плане 18 см2. Вариант II 1. Найдите длину окружности, если её диаметр равен 15 дм. Число п округлите до десятых. 2. Расстояние между двумя пунктами на карте равно 8,2 см. Определите расстояние между этими пунктами на местности, если масштаб карты 1:10000. 3. Найдите площадь круга, радиус которого равен 8 см. Число п округлите до десятых. 4. Цена товара понизилась с 57,5 до 48,3 р. На сколько процентов понизилась цена товара? 5. Прямоугольный земельный участок изображен на плане в масштабе 1:400. Какова площадь земельного участка, если площадь его изображения на плане 16 см2? Контрольная работа №9 Вариант I 1.Отметьте на координатной прямой точки А(-5), С(3), Е(4,5), К(-3), N(-0,5), S(6). 2. Сравните числа: а) 2,8 и -2,5; б) -4,1 и -4; в)  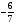 и и 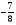 , г) 0 и , г) 0 и 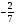 3. Найдите значение выражения: а) |-6,7| + |-3,2|; б) |2,73|:|-2,1| в) 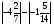 4. Решите уравнение: а) –х=3,7 б) –у=-12,5 в) |х|=6 5. Сколько целых решений имеет неравенство -18 Вариант II 1.Отметьте на координатной прямой точки B(-6), D(-3,5), F(4), M(0,5), P(-4), T(5). 2. Сравните числа: а) -4,6 и 4,1, б) -3 и -3,2, в)  , г) , г)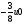 3. Найдите значение выражения: а) |-5,2| + |3,6|, б) |-4,32|:| - 1,8|, в) 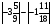 4. Решите уравнение: а) –у = 2,5 б) –х = -4,8 в) |y| = 8 5. Сколько целых решений имеет неравенство -26 Контрольная работа №10 Вариант I 1. Выполните действие: а) 42-45 г) 17-(-8) б) -16-31 д) -3,7-2,6 в) -15+18 е) 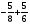 2. Найдите расстояние между точками координатной прямой: а) М(-13) и К(-7) б) В(2,6) и Т(-1,2) 3. Решите уравнение: а) х – 2,8 = -1,6 б) 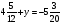  4. Цена товара повысилась с 84р. до 109,2р. На сколько процентов повысилась цена товара? 5. Решите уравнение |x-3|=6 Вариант II 1. Выполните действие: а) -39+42 г) -16 – (-10) б) -17-20 д) 4,3 – 6,2 в) 28-35 е) 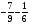 2. Найдите расстояние между точками координатной прямой: а) N(-4) и С(-9); б) А(-6,2) и Р(0,7) 3. Решите уравнение: а) 3,2 – х = -5,1 б) 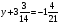 4. Цена товара повысилась с 92р. до 110,4 р. На сколько процентов повысилась цена товара? 5. Решите уравнение |y + 2| = 8 Контрольная работа №11 Вариант I 1. Выполните умножение: а) -8∙12 в) 0,8∙(-2,6) б) -14∙(-11) г) 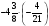 2. Выполните деление: а) 63:(-21) в) -0,325:1,3 б) -24:(-6) г) 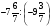 3. Решите уравнение: а) 1,8у = -3,69б) х:(-2,3) = -4,6 4. Представьте числа 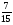 и и 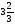 в виде периодических дробей. Запишите приближенные значения данных чисел, округлив периодические дроби до сотых. в виде периодических дробей. Запишите приближенные значения данных чисел, округлив периодические дроби до сотых.5. Сколько целых решений имеет неравенство |x| <64? Вариант II 1. Выполните умножение: а) 14∙(-6) в) -0,7∙3,2 б) -12∙(-13) г) 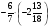 2. Выполните деление: а) -69:23 в) 0,84:(-2,4) б) -35:(-7) г) 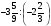 3. Решите уравнение а) -1,4х =-4,27 б) у:3,1 = -6,2 4. Представьте числа 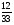 и и 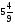 в виде периодических дробей. Запишите приближенные значения данных чисел, округлив периодические дроби до сотых. в виде периодических дробей. Запишите приближенные значения данных чисел, округлив периодические дроби до сотых.5. Сколько целых решений имеет неравенство |y|<72? Контрольная работа №12 Вариант I 1. Найдите значение выражения: а) раскрыв скобки: 34,4 – (18,1 – 5,6) + (-11,9 +8) б) применив распределительное свойство умножения: 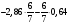 2. Упростите выражение: а) 4m – 6m – 3m+7+m б) -8(к-3)+4(к-2)-2(3к+1) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 2