Знать:
понятие плоского угла, дополнительных углов; определения центрального угла, дуги окружности, градусной меры дуги окружности, угла, вписанного в окружность;
формулировку теоремы о связи градусных мер центрального и вписанного углов;
свойство вписанных углов в окружность.
Уметь:
по чертежу определять дополнительные углы, центральные и вписанные в окружность;
строить центральный и вписанный в окружность углы;
записывать пропорциональность отрезков хорд и секущих окружности.
П.107
|
12
|
Вписанный угол; величина вписанного угла.
|
|
|
|
П.107
|
13
|
Метрические соотношения в окружности: свойства секущих, касательных, хорд.
|
|
|
|
П.108
|
14
|
Метрические соотношения в окружности: свойства секущих, касательных, хорд.
|
|
|
|
П.108
|
15
|
Метрические соотношения в окружности: свойства секущих, касательных, хорд.
|
|
|
|
П.108
|
16
|
Контрольная работа №2
|
|
|
|
|
Решение треугольников – 9 ч
|
17
|
Теорема косинусов; примеры применения для вычисления элементов треугольника
|
|
|
|
Знать:
формулировки теоремы косинусов и следствий из нее, утверждения о свойстве диагоналей параллелограмма;
формулировки теоремы синусов и следствия из нее о соотношении между сторонами и углами треугольника;
Уметь:
доказывать теорему косинусов, записывать в виде равенства теорему косинусов применительно к данному треугольнику, по трем данным сторонам находить его углы, по данным двум сторонам треугольника и углу между ними находить третью сторону, применять теорему косинусов и следствия из нее к решению задач;
доказывать теорему синусов, записывать ее формулировку символически и составлять пропорции для сторон и углов данного треугольника, решать задачи;
для каждой из трех основных задач проводить решение в общем виде и для конкретных треугольников.
|
|
18
|
Теорема косинусов; примеры применения для вычисления элементов треугольника.
|
|
|
|
|
19
|
Теорема синусов; примеры применения для вычисления элементов треугольника.
|
|
|
|
|
20
|
Теорема синусов; примеры применения для вычисления элементов треугольника.
|
|
|
|
|
21
|
Теорема косинусов и теорема синусов; примеры их применения для вычисления элементов треугольника.
|
|
|
|
|
22
|
Теорема косинусов и теорема синусов; примеры их применения для вычисления элементов треугольника.
|
|
|
|
|
23
|
Теорема косинусов и теорема синусов; примеры их применения для вычисления элементов треугольника.
|
|
|
|
|
24
|
Теорема косинусов и теорема синусов; примеры их применения для вычисления элементов треугольника.
|
|
|
|
|
25
|
Контрольная работа №3
|
КЗУ
|
КР
|
Итог.
|
|
Многоугольники – 12 ч
|
26
|
Ломаная. Длина ломаной
|
|
|
|
Знать:
что длина ломаной не меньше длины отрезка, соединяющего ее концы;
сумма углов выпуклого n-угольника равна 180º∙(n-2), а сумма внешних углов выпуклого n-угольника равна 360º;определения правильного многоугольника, многоугольника, вписанного в окружность, многоугольника, описанного около окружности;
что для каждого правильного многоугольника существует окружность, вписанная в него, и окружность, описанная около него, и что такие окружности имеют общий центр, который находится в точке пересечения биссектрис правильного многоугольника;
формулы, связывающие радиус описанной окружности и радиус вписанной окружности со стороной a правильного n-угольника для n=3,4,6; что периметры правильных n- угольников относятся как радиусы описанных (вписанных) окружностей, отношение длины окружности к ее диаметру одно и тоже (π), что такое радианная мера угла, какой центральный угол является углом в 1 радиан, что радианная мера угла 180º равна π радианам.
Уметь:
изображать ломаную, называть по рисунку ее элементы, проводить доказательство теоремы;
доказывать теорему о сумме углов выпуклого n-угольника, решать задачи;
проводить доказательство теоремы;
выводить формулы для R, r, конкретизировать их для правильного многоугольника с заданным числом сторон, выводить частные случаи этих формул для n=3,4,6 без использования общей формулы;составлять пропорцию, связывающую градусную и радианную меры угла, и использовать ее для перевода градусной меры угла в радианную и наоборот.
|
П.113
|
27
|
Выпуклые многоугольники. Периметр многоугольника. Сумма углов выпуклого многоугольника. Вписанные и описанные многоугольники. Правильные многоугольник
|
|
|
|
П.114
|
28
|
Выпуклые многоугольники. Сумма углов выпуклого многоугольника. Правильные многоугольники
|
|
|
|
П.114,115
|
29
|
Формулы для радиусов вписанных и описанных окружностей правильных многоугольников
|
|
|
|
П.116
|
30
|
Формулы для радиусов вписанных и описанных окружностей правильных многоугольников
|
|
|
|
|
31
|
Формулы для радиусов вписанных и описанных окружностей правильных многоугольников
|
|
|
|
|
32
|
Вписанные и описанные многоугольники. Правильные многоугольники.
|
|
|
|
|
33
|
Вписанные и описанные многоугольники. Правильные многоугольники.
|
|
|
|
|
34
|
Вписанные и описанные многоугольники. Правильные многоугольники.
|
|
|
|
|
|
35
|
Решение задач. Вписанные и описанные многоугольники. Правильные многоугольники.
|
|
|
|
|
36
|
Решение задач. Вписанные и описанные многоугольники. Правильные многоугольники.
|
|
|
|
|
37
|
Контрольная работа №4
|
КЗУ
|
КР
|
Итог.
|
|
Площади фигур – 18 ч
|
38
|
Понятие о площади плоских фигур. Равносоставленные и равновеликие фигуры. Площади фигур
|
|
|
|
Знать:
свойства площади простой фигуры, формулу площади прямоугольника, параллелограмма, трапеции, треугольника;
площади подобных фигур относятся как квадраты их соответствующих линейных размеров, что с увеличением (уменьшением) линейных размеров фигуры в k раз ее площадь увеличивается (уменьшается) в k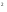 раз; раз;
- определение круга, формулу площади круга. Что такое круговой сектор и круговой сегмент.
Уметь:
вывести формулу площади прямоугольника для случая, когда длины сторон – рациональные числа;
провести доказательство справедливости формул для параллелограмма, трапеции, треугольника, применять их для решения задач;
использовать формулы площади треугольника через синус, Герона, радиуса описанной и вписанной окружностей при решении задач;
находить отношение площадей подобных фигур по известным длинам пары соответствующих элементов этих фигур;
вычислять площади круга, кругового сектора и кругового сегмента.
|
|
39
|
Площадь прямоугольника.
|
|
|
|
П.122
|
40
|
Площадь параллелограмма
|
|
|
|
П.123
|
41
|
Площадь параллелограмма
|
|
|
|
П.123
|
42
|
Площадь треугольника. Формулы, выражающие площадь треугольника через две стороны и угол между ними
|
|
|
|
|
43
|
Формулы, выражающие площадь треугольника. Формула Герона
|
|
|
|
П.125
|
44
|
Формулы, выражающие площадь треугольника: через две стороны и угол между ними, через периметр и радиус вписанной окружности
|
|
|
|
|
45
|
Площадь параллелограмма, треугольника и трапеции (основные формулы).Площадь четырехугольника.
|
|
|
|
П.126
|
46
|
Площадь параллелограмма, треугольника и трапеции (основные формулы).
|
|
|
|
|
47
|
Решение задач. Площадь четырехугольника.
|
|
|
|
|
48
|
Контрольная работа №5
|
КЗУ
|
КР
|
Итог.
|
|
49
|
Формулы для радиусов вписанной и описанной окружностей треугольника
|
|
|
|
П.127
|
50
|
Формулы для радиусов вписанной и описанной окружностей треугольника
|
|
|
|
П.127
|
51
|
Формулы для радиусов вписанной и описанной окружностей треугольника
|
|
|
|
П.127
|
52
|
Площади подобных фигур, Связь между площадями подобных фигур.
|
|
|
|
П.128
|
53
|
Площадь круга
|
|
|
|
П.129
|
54
|
Площадь круга
|
|
|
|
П.129
|
55
|
Контрольная работа №6 по теме «Площади фигур»
|
КЗУ
|
КР
|
Итог.
|
|
Элементы стереометрии – 8 ч
|
56
|
Аксиомы стереометрии. Параллельность прямых и плоскостей в пространстве.
|
|
|
|
Знать:
Аксиомы стереометрии, основные сведения о взаимном расположении прямой и плоскости, теорему о трех перпендикулярах;
понятие о многогранниках и телах вращения, формулы объемов их;
Уметь: применять теорию к решению задач.
|
П.130,131
|
57,58
|
Перпендикулярность прямых и плоскостей в пространстве.
|
|
|
|
П.132
|
59,60
|
Перпендикулярность прямых и плоскостей в пространстве. Перпендикуляр и наклонная. Теорема о трех перпендикулярах.
|
|
|
|
П.132
|
61
|
Многогранники
|
|
|
|
П.133
|
62,63
|
Тела вращения. Объемы тел вращения. Сфера. Шар. Шаровой сегмент
|
|
|
|
П.134
|
Повторение – 5 ч
|
64
|
Повторение «Решение треугольников»
|
|
|
|
|
|
65
|
Повторение «Многоугольники»
|
|
|
|
|
66
|
Повторение «Площади фигур»
|
|
|
|
|
67
|
Итоговая контрольная работа
|
КЗУ
|
КР
|
Итог.
|
|
68
|
Анализ контрольной работы
|
|
|
|
|
 Скачать 433.18 Kb.
Скачать 433.18 Kb.