Теорема Пифагора
 Скачать 89 Kb. Скачать 89 Kb.
|
| МБОУСОШ №3 с. Безопасное Урок алгебры в 8 классе на тему: «Теорема Пифагора» учитель математики Мокроусова.Е.Н. 2013 г Содержание Теорема Пифагора. Применение теоремы Пифагора к решению задач. Цель изучения
Прогнозируемый результат
План урока
Ход урока:
Открыть новые тетради, записать число и тему урока.
Сегодня ребята у нас будет не простой урок, а урок – путешествие. Мы с вами познакомимся с самой важной теоремой в математике и совершим круиз на необычном корабле, который умеет перевозить своих пассажиров не только в разные страны, но и в разные времена. А отправимся мы вслед за историей теоремы Пифагора по следующему маршруту
Для того, чтобы наше путешествие прошло без происшествий, я прошу всех занять свои каюты, мы с вами сегодня не просто пассажиры – а исследователи, учёные – математики, историки и литераторы. Прежде, чем отправится в плавание, нужно потренироваться перед долгим путешествием, и вспомнить всё, что нам может пригодиться в дороге. 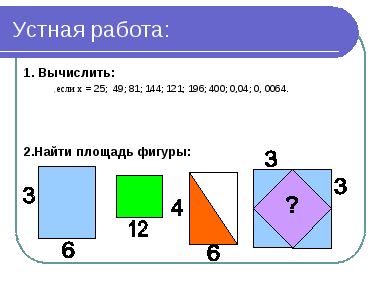
Хорошо, я вижу, что к путешествию вы готовы. Но на нашем корабле возникла небольшая проблема: Задача  Если мы не сможем определить точное значение, то не сможем отправиться в путь. Для решения этой проблемы мы проведём практическую работу исследовательского характера, предложив учащимся задание по группам: построить прямоугольные треугольники с катетами 12 см и 5 см; 6 см и 8 см; 8 см и 15 см и измерить гипотенузу. 4. Сообщения о Пифагоре Самосском и истории открытия теоремы. Сейчас мы узнаем побольше о том, кто такой Пифагор и почему эта теорема была названа его именем (сообщение учащегося) 1 учащийся: ПИФАГОР САМОССКИЙ (ок. 580 – ок. 500 г. до н.э.) О жизни Пифагора известно немного. Он родился в 580 г. до н.э. в Древней Греции на острове Самос, который находится в Эгейском море у берегов Малой Азии, поэтому его называют Пифагором Самосским. Родился Пифагор в семье резчика по камню, который сыскал скорее славу, чем богатство. Ещё в детстве он проявлял незаурядные способности, и когда подрос, неугомонному воображению юноши стало тесно на маленьком острове. Пифагор перебрался в город Милеет и стал учеником Фалеса, которому в то время шёл восьмой десяток. Мудрый учёный посоветовал юноше отправиться в Египет, где сам, когда-то изучал науки. Перед Пифагором открылась неизвестная страна. Его поразило то, что в родной Греции боги были в образе людей, а египетские боги – в образе полулюдей-полуживотных. Знания были сосредоточены в храмах, доступ в которые был ограничен. Пифагору потребовались годы, чтобы глубоко изучить египетскую культуру прежде, чем, ему было разрешено познакомиться с многовековыми достижениями египетской науки. Когда Пифагор постиг науку египетских жрецов, то засобирался домой, чтобы там создать свою школу. Жрецы, не желавшие распространения своих знаний за пределы храмов, не хотели его отпускать. С большим трудом ему удалось преодолеть эту преграду. Однако по дороге домой, Пифагор попал в плен и оказался в Вавилоне. Вавилоняне ценили умных людей, поэтому он нашёл своё место среди вавилонских мудрецов. Наука Вавилона была более развитой, нежели египетская. Наиболее поразительными были успехи алгебры. Вавилоняне изобрели и применяли при счёте позиционную систему счисления, умели решать линейные, квадратные и некоторые виды кубических уравнений. Пифагор прожил в Вавилоне около десяти лет и в сорокалетнем возрасте вернулся на родину. Но на острове Самос он оставался недолго. В знак протеста против тирана Поликрата, который тогда правил островом, поселился в одной из греческих колоний Южной Италии в городе Кротоне. Там Пифагор организовал тайный союз молодёжи из представителей аристократии. В этот союз принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками. В школе существовал декрет, по которому авторство всех математических работ приписывалось учителю. Пифагорейцами было сделано много важных открытий в арифметике и геометрии, в том числе:
Известно также, что кроме духовного и нравственного развития учеников Пифагора заботило их физическое развитие. Он не только сам участвовал в Олимпийских играх и два раза побеждал в кулачных боях, но и воспитал плеяду великих олимпийцев. Около сорока лет учёный посвятил созданной им школе и, по одной из версий, в возрасте восьмидесяти лет Пифагор был убит в уличной схватке во время народного восстания. После его смерти ученики окружили имя своего учителя множеством легенд. 2 учащийся: Как утверждают все античные авторы, Пифагор первый дал полноценное доказательство теоремы, носящей его имя. К сожалению, мы не знаем, в чем оно состояло, потому что древние математики и писатели об этом умалчивают, а от самого Пифагора и ранних пифагорейцев до нас не дошло ни одного письменного документа. Только позже у Евклида было обнаружено доказательство этой теоремы. У Евклида эта теорема гласит (дословный перевод): "В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол". В настоящее время известно, что эта теорема не была открыта Пифагором. Однако одни полагают, что Пифагор первым дал ее полноценное доказательство, а другие отказывают ему и в этой заслуге. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих "Начал". С другой стороны, Прокл утверждает, что доказательство в "Началах" принадлежит самому Евклиду. Как мы видим, история математики почти не сохранила достоверных данных о жизни Пифагора и его математической деятельности. Рассказывают – это, конечно, лишь легенда, – что, когда Пифагор доказал свою знаменитую теорему, он отблагодарил богов, принеся им в жертву сто быков. Этот рассказ о жертвоприношении, сообщаемый Диогеном и Плутархом, скорее всего, вымышлен, ибо, как известно, Пифагор был вегетарианцем и непримиримым противником убоя и пролития крови животных. Учитель: В настоящее время их насчитывается более ста. Большинство способов её доказательства сводятся к разбиению квадратов на более мелкие части. На сайтеhttps://th-pif.narod.ru вы сможете познакомиться с 30 доказательствами этой теоремы, некоторые из которых мы будет чуть позже рассматривать на уроках геометрии. Вероятно, факт, изложенный в теореме Пифагора, был сначала установлен для равнобедренных прямоугольных треугольников. Квадрат, построенный на гипотенузе, содержит четыре треугольника. А на каждом катете построен квадрат, содержащий два треугольника. Из рисунка видно, что площадь квадрата, построенного на гипотенузе равна сумме площадей квадратов, построенных на катетах. Такие стишки придумывали школьники при изучении этой теоремы и даже рисовали шаржи. Например, такие: 5 Путешествие в Древний Китай. Как свидетельствуют летописи, в Древнем Китае уже около 2200 года до н.э. для треугольника со сторонами 3, 4, 5 было найдено правило «гоу-гу», с помощью которого можно было по известным гипотенузе и одному из катетов находить другой неизвестный катет, а также гипотенузу. 6 Путешествие в Древний Египет 2300 г. до н. э. В древнем Египте в это время активно велось строительство храмов, гробниц и даже была такая профессия -гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5. 7 Практическая работа по построению прямого угла с помощью египетского треугольника Давайте проверим, действительно ли это так? Какой длины нужно отмерить верёвку, чтобы построить треугольник? 3+4+5=12см. Отмерим с помощью линейки 3 см, 4 см, закрепим с помощью пластилина на картоне стороны. Что мы получили? Получили прямоугольный треугольник со сторонами 3, 4 и 5 ед. Это единственный прямоугольный треугольник, стороны которого равны трём последовательным натуральным числам. Его часто называют египетским треугольником, так как он был известен ещё древним египтянам. Они использовали этот треугольник в "правиле верёвки" для построения прямых углов при закладке зданий, храмов, алтарей. 8 Путешествие в Индию В самом древнем индийском геометрическом сборнике «Сульвасутра» («Правила веревки», 600 год до н.э.), представляющем собой своеобразную инструкцию по сооружению алтарей в храмах, даются правила построения прямых углов при помощи веревки с узлами, расстояния между которыми равны 15, 36 и 39 падас (мера длины Первое упоминание о теореме Пифагора в России было сделано в 18 веке, в первом русском переводе евклидовых "Начал", сделанном Ф. И. Петрушевским, там теорема Пифагора изложена так: "В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол". После этого, она уже встречается в задачнике Магницкого: 9 Наше время:
10 Работа с тестами. Т 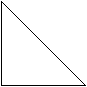 ест по теме: «Теорема Пифагора» ест по теме: «Теорема Пифагора»1  ) )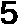 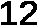 А) 7 А) 7Б) 13 В) 17 Г) 169  2    ) А) 2 ) А) 2Б) 164 В) 18 Г) 6 11 Подведение итога: Как звучит теорема Пифагора? Что такое египетский треугольник? 12 Д/З с. 69-71 №276 | ||||||||||||||||||||||
