№ урока
|
Содержание изучаемого материала
|
Знания и умения
|
Основное содержание
|
Дата проведения
|
По плану
|
фактически
|
|
Повторение(4 часа)
|
1
|
Тригонометрические функции, их свойства и графики
|
тригонометрические функции числового аргумента, тригонометрические соотношения одного аргумента, тригонометрические функции:  , ,  , ,  , ,  , график и свойства функций , график и свойства функций
|
Учащиеся умеют свободно читать графики, отражать свойства функции на графике.
|
|
|
2
|
Преобразование тригонометрических выражений Тригонометрические уравнения
|
тригонометрические формулы одного, двух и половинного аргумента, формулы приведения, формулы перевода произведения функций в сумму и наоборот, метод разложения на множители, однородные тригонометрические уравнения первой и второй степени, алгоритм решения уравнения
|
Умеют использовать формулы, содержащие тригонометрические выражения для выполнения соответствующих расчетов; преобразовывать формулы, выражая одни тригонометрические функции через другие. Учащиеся умеют решать простейшие тригонометрические уравнения. Владеют основными способами решения тригонометрических уравнений..
|
|
|
3
4
|
Производная, ее применение для исследования функции на монотонность
|
построение графика, возрастающая функция, убывающая функция, монотонность
|
Умеют находить производные элементарных функций, применяя таблицу производных и правила дифференцирования. Знают и умеют осуществлять алгоритм исследования функции на монотонность
|
|
|
Степени и корни. Степенные функции(15 часов)
|
5
6
|
Понятие корня n-й степени из действительного числа
|
Знать: понятие корня n-ой степени из неотрицательного числа, корня нечетной степени из отрицательного числа.
Уметь: вычислять корни n-ой степени из действительного числа, решать уравнения, корни которых являются корнями n-ой степени из действительного числа.
|
Определения: корня n-ой степени из неотрицательного числа, корня нечетной степени n из отрицательного числа, понятие радикала, решение уравнений с радикалами.
|
|
|
7
8
|
Функции у=n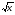 , их свойства и графики , их свойства и графики
|
Знать: что представляет собой график функции у=n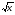 , при n – четном и n – нечетном, свойства функции у=n , при n – четном и n – нечетном, свойства функции у=n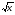
Уметь: строить графики и решать уравнения и неравенства с радикалами.
|
Функции у=n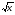 , их свойства и графики. Построение графиков функций с радикалами, графическое решение уравнений и неравенств с радикалами. , их свойства и графики. Построение графиков функций с радикалами, графическое решение уравнений и неравенств с радикалами.
|
|
|
9
10
|
Свойства корня n-й степени
|
Знать: теоремы выражающее свойства корня n-й степени
Уметь: доказывать теоремы и применять их при упрощении выражений
|
5 теорем, выражающих свойства корня n-й степени; упрощение выражений, нахождение значений числовых выражений, содержащих корни n-й степени
|
|
|
11
12
13
|
Преобразование выражений содержащих радикалы
|
Знать: что такое внесение/вынесение множителя под/за знак радикала, понятие иррационального выражения
Уметь: выносить множитель за знак радикала, вносить множитель под знак радикала, упрощать иррациональные выражения, используя свойства извлечения корня n-й степени из действительного числа
|
Понятие иррационального выражения, операции внесения и вынесение множителя под/за знак радикала, упрощение иррациональных выражений, разложение на множители, сокращение дробей
|
|
|
14
|
Контрольная работа № 1 «Степени и корни. Степенные функции»
|
|
|
15
16
17
18
|
Обобщение понятия о показателе степени
|
Знать: определение степени с любым рациональным показателем, понятие иррационального уравнения, основные методы решения иррациональных уравнений
Уметь: представлять заданное выражение в виде степени с рациональным показателем, степень с дробным показателем в виде корня, упрощать выражения содержащие степени с дробным показателем
|
Понятие степени с рациональным показателем, определения, относящиеся к операции возведения в степень, понятие иррационального уравнения и основные методы решения иррациональных уравнений; упрощение выражений со степенями, нахождение значений числовых выражений со степенями и буквенных выражений со степенями при заданных значениях переменной
|
|
|
19 20
21
|
Степенные функции, их свойства и графики
|
Знать: определение степенной функции, свойства функции y=xr, где r – любое действительное число, свойства степенной функции, теорему о производной степенной функции, формулу для интегрирования степенной функции
Уметь: строить график степенной функции для любого рационального показателя r, исследовать степенную функцию на четность, ограниченность, монотонность и экстремумы, составлять уравнения касательной, находить наибольшее и наименьшее значения функции на промежутке, с помощью производной, вычислять первообразные , интегралы и площади плоских фигур
|
Эскизы графика степенной функции y=xr для любого рационального показателя r:
при четном натуральном значении r график похож на параболу, а при нечетном, большем чем 1,— на кубическую параболу;
при нечетном отрицательном целом значении r график похож на гиперболу, а при четном состоит как бы из 2-х ветвей гиперболы, симметричных относительно оси y;
при положительном дробном значении r трафик похож на одну ветвь параболы, которая ориентирована вверх при r>1 и вправо – при 0
при отрицательном дробном значении r график похож на одну ветвь гиперболы;
график любой степенной функции проходит через точку (1; 1).
|
|
|
|
Показательная и логарифмическая функции(24 часа)
|
22
23
24
|
Показательная функция ,ее свойства и график
|
Знать: определение показательной функции, ее свойства; теоремы на которых базируется теория решения показательных уравнений и нера�венств
Уметь: строить графики показатель�ных функций, применять свойства функции при сравнении степеней, исследовании функции на монотон�ность, решении уравнений и нера�венств
|
Определение показательной функции, ее свойства и теоремы на которых базируется теория решения показательных уравнений и неравенств
|
|
|
25
26
27
|
Показательные уравнения
|
Знать: определение показательного уравнения, методы решения показательных уравнений
Уметь: решать показательные уравнения, применяя изученные методы
|
Понятие показательного уравнения, 3 метода решения показательных уравнений (функционально-графический метод, метод уравнивания показателей, метод введения новой переменной)
|
|
|
28
29
|
Показательные неравен�ства
|
Знать: определение показательного неравенства, теорему, на которой базируется решение показательных неравенств
Уметь: применять теорему при решении показательных неравенств
|
Понятие показательного неравенства, теорема, на которой базируется решение показательных неравенств, решение показательных неравенств
|
|
|
30
|
Контрольная работа
№ 3 «Показательная функция»
|
|
|
31
32
|
Понятие логарифма
|
Знать: определение логарифма, понятия десятичного и натурального логарифмов, обозначения логарифмов, определение операции логарифмирования
Уметь: вычислять логарифмы от заданных чисел и выражений
|
Понятие логарифма, основные формулы и основное логарифмическое тождество, вычисление логарифмов от заданных чисел и выражений
|
|
|
33
34
35
|
Функция y=logax, ее свойства и график
|
Знать: определение логарифмической функции, свойства функции в зависимости от основания логарифма
Уметь: строить и читать графики логарифмической функции, находить наибольшее и наименьшее значения функции на заданном промежутке
|
Понятие логарифмической функции, ее свойства и графики в зависимости от основания логарифма, построение и чтение графиков логарифмической функции, нахождение наибольшего и наименьшего значения функции на заданном промежутке
|
|
|
36
37
38
|
Свойства логарифмов
|
Знать: основные теоремы, выражающие свойства логарифмов, определения операций логарифмирования и потенцирования, понятия дробной части и мантиссы десятичного логарифма
Уметь: доказывать основные теоремы, выражающие свойства логарифмов, применять свойства логарифмов при вычислении логарифмов, упрощении логарифмических выражений, решении логарифмических уравнений
|
Теоремы: логарифм произведения двух положительных чисел, частного, степени, равенства двух логарифмов, понятие дробной части и мантиссы десятичного логарифма; применение теорем при вычислении логарифмов, упрощении логарифмических выражений, решении логарифмических уравнений
|
|
|
39
40
41
42
43
|
Логарифмические урав�нения
|
Знать: определение логарифмического уравнения, теорему, применяемую при решении логарифмических уравнений, основные методы решения логарифмических уравнений
Уметь: применять рассмотренные методы при решении логарифмических уравнений
|
Определение логарифмического уравнения, основные методы решения логарифмических уравнений: функционально-графический, метод потенцирования, метод введения новой переменной, метод логарифмирования
|
|
|
44
|
Контрольная работа
№ 4 «Логарифмическая функция»
|
|
|
|
|
45
46
47
|
Логарифмические неравенства
|
Знать: определение логарифмического неравенства, теорему перехода от логарифмического неравенства к равносильной ему системе неравенств
Уметь: применять рассмотренную теорему при решении логарифмических неравенств
|
Определение логарифмического неравенства, теорема перехода от логарифмического неравенства к равносильной ему системе неравенств; применение теоремы при решении логарифмических неравенств и систем логарифмических неравенств
|
|
|
48
49
|
Переход к новому основанию логарифма
|
Знать: Формулу перехода от логарифма по одному основанию к логарифму по другому основанию и частные случаи этой формулы
Уметь: использовать эту формулу при решении логарифмических уравнений и неравенств.
|
Формула перехода от логарифма по одному основанию к логарифму по другому основанию и частные случаи этой формулы
|
|
|
50
51
|
Дифференцирование показательной и логарифмической функций
|
Знать: что такое число е, понятие зкспоненты, свойства функции у=ех, формулы дифференцирования и интегрирования функции у=ех, определение натурального логарифма, функции у = lnх, ее свойства и график, формулы дифференцирования и интегрирования функций у=lnх,
у=ах, у=logах
Уметь: находить производные и интегралы
|
Понятия числа е, экспоненты, натурального логарифма, функции у=lnх, графики , свойства, формулы дифференцирования и интегрирования функций у=ех, у=lnх.. Нахождение производных, интегралов функций, содержащих ех, lnх, решение уравнения, неравенства и задачи на вычисление площадей фигур и касательную с применением этих формул
|
|
|
52
|
Контрольная работа
№ 5 «Показательная и логарифмическая функция»
|
|
|
Первообразная и интеграл(7 часов)
|
53
54
55
56
|
Первообразная и неопределенный интеграл
|
Знать: понятие первообразной, формулы для отыскания первообразных, правила отыскания первообразных; определение неопределенного интеграла, таблицу основных неопределенных интегралов, правила интегрирования
Уметь: доказывать, что функция является первообразной, находить множество первообразных для заданной функции, находить первообразную, график которой проходит через заданную точку, находить неопределенный интеграл, используя правила интегрирования и таблицу основных неопределенных интегралов
|
Понятие первообразной, неопределенного интеграла, правила для отыскания первообразных, правила интегрирования, формулы для отыскания первообразных и неопределенных интегралов; нахождение множества первообразных для заданной функции, решение задач по нахождению первообразной, график которой проходит через заданную точку, решение задачи по нахождению неопределенных интегралов
|
|
|
57
58
59
60
61
|
Определенный интеграл
|
Знать: понятие определенного интеграла, геометрический и физический смысл определенного интеграла, формулу Ньютона-Лейбница.
Уметь: вычислять определенный интеграл, вычислять площади плоских фигур с помощью определенного интеграла.
|
3 задачи, приводящие к понятию определенного интеграла: о вычислении площади криволинейной трапеции, о вычислении массы стержня, о перемещении точки, понятие определенного интеграла, формулу Ньютона-Лейбница. Вычисление определенных интегралов, площади плоских фигур с помощью определенного интеграла.
|
|
|
62
|
Контрольная работа
№7 «Первообразная и интеграл»
|
|
|
Элементы математической статистики, комбинаторики и теории вероятностей(12 часов)
|
63
64
65
|
Статистическая обработка данных
|
классическая вероятностная схема, вероятность событий, геометрическая вероятность, равновозможные исходы, предельный переход
|
Знают классическую вероятностную схему для равновозможных испытаний;
знают правило геометрических вероятностей. Используют компьютерные технологии для создания базы данных.
|
|
|
66
67
68
|
Простейшие вероятностные задачи
|
схема Бернулли, теорема Бернулли, биноминальное распределение, многоугольник распределения
|
Учащиеся решают вероятностные задачи, используя вероятностную схему Бернулли, теорему Бернулли, понятие многогранник распределения. Используют для решения познавательных задач справочную литературу.
|
|
|
69
70
|
Сочетания и размещения
|
обработка информации, таблицы распределения данных, графики распределения данных, паспорт данных, числовые характеристики, таблица распределения, частота варианты, гистограмма распределения, мода, медиана, среднее ряда данных.
|
Знают понятия: общий ряд данных, выборка, варианта, кратность варианты, таблица распределения, частота варианты, график распределения частот, треугольник Паскаля. Находят частоту события, используя собственные наблюдения и готовые статистические данные, понимают статистические утверждения, встречающиеся в повседневной жизни.
|
|
|
71
72
73
|
Формула бинома Ньютона
|
статистическая устойчивость, гауссова кривая, алгоритм использования гауссовой кривой в приближенных вычислениях, закон больших чисел
|
Знают, график какой функции называется гауссовой кривой; алгоритм использования кривой нормального распределения и функции площади под гауссовой кривой в приближенных вычислениях, о законе больших чисел. Решают вероятностные задачи, используя знания о гауссовой кривой, алгоритме использования кривой нормального распределения и функции площади под гауссовой кривой в приближенных вычислениях, о законе больших чисел.
|
|
|
74
75
76
|
Случайные события и их вероятности
|
Дать определение относительной частоты случайного события. Сформулировать классическое определение вероятности случайного события
|
Уметь вычислять вероятность случайного события при классическом подходе
|
|
|
77
|
Решение практических задач
|
|
|
|
|
78
|
Контрольная работа №8
«Элементы теории вероятностей и математической статистики»
|
Уметь: решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул,
вычислять, в простейших случаях, вероятности событий, использовать приобретенные знания и умения в практической деятельности и повседневной жизни: для анализа реальных числовых данных, представленных в виде диаграмм, графиков; для анализа информации статистического характера.
|
Учащиеся свободно демонстрируют умение решать задачи на применение элементов математической статистики и элементов теории вероятностей
|
|
|
Уравнения и неравенства. Системы уравнений и неравенств(17 часов)
|
79
80
81
|
Равносильность уравнений
|
Знать: определения равносильных уравнений, уравнения- следствия, постороннего корня, теоремы о равносильности уравнений, причины потери корней при решении уравнений
Уметь: преобразовывать данное уравнение в уравнение- следствие, доказывать равносильность уравнений
|
Определения равносильных уравнений, уравнения- следствия, постороннего корня, теоремы о равносильности уравнений; преобразование данных уравнений в уравнение- следствие, определение посторонних корней
|
|
|
82
83
84
|
Общие методы решения уравнений
|
Знать: 4 общих метода решения уравнений
Уметь: использовать рассмотренные методы при решении уравнений
|
Общие методы решения уравнений: замена уравнения h(f(x))=h(g(x)) уравнением
f(x)=g(x), метод разложения на множители, метод введения новых переменных, функционально- графический метод
|
|
|
85
86
87
88
89
|
Решение неравенств с одной переменной
|
Знать: определения равносильных неравенств, неравенства- следствия, теоремы о равносильности неравенств, определения системы неравенств, совокупности неравенств
Уметь: доказывать равносильность неравенств, решать неравенства, применяя теоремы о равносильности неравенств, решать системы и совокупности неравенств, иррациональные неравенства и неравенства с модулями
|
Понятия: равносильных неравенств, неравенства- следствия, системы неравенств, совокупности неравенств. Теоремы о равносильности неравенств. Применение теорем о равносильности неравенств при решении неравенств с одной переменной, решение систем и совокупности неравенств, иррациональные неравенства, неравенства с модулями
|
|
|
90
91
92
93
94
|
Уравнения и неравенства с двумя переменными.
Системы уравнений
|
Знать: понятия системы уравнений, решения системы, равносильных систем, основные методы решения систем
Уметь: применять изученные методы при решении систем, решать текстовые задачи с помощью систем уравнений
|
Понятие системы уравнений, решения системы уравнений, равносильных систем. Основные методы решения систем: подстановки, алгебраического сложения, введения новых переменных, графического, метод умножения, метод деления.
|
|
|
95
96
97
98
99
100
|
Уравнения и неравенства с параметрами
|
Знать: что такое уравнение и неравенство с параметрами и как рассуждают при решении уравнений и неравенств с параметрами
Уметь: решать простейшие уравнения и неравенства с парамет�рами
|
Понятие уравнения и нера�венства с параметрами. Решение уравнений и неравенств с параметрами
|
|
|
101
102
|
Контрольная работа № 10 «Уравнения и неравенства. Системы уравнений и неравенств»
|
Знать: понятия уравнения, неравенства, системы уравнений,
Уметь: применять изученные методы при решении уравнений, неравенств, систем, решать текстовые задачи
|
|
|
|
Повторение(30 часов)
|
103
104
|
Повторение. Преобразование выражений, содержащих степени с рациональным показателем.
|
Уметь: выполнять преобразование выражений, содержащих степени с рациональным показателем.
|
|
|
|
105
106
|
Повторение. Решение неравенств методом интервалов
|
Уметь: решать неравенства методом интервалов
|
|
|
|
107
108
|
Повторение .Арифметическая,геометрическая прогрессия.
|
Уметь: решать задачи на арифметическую, геометрическую прогрессию.
|
|
|
|
109
110
|
Повторение. Решение тригонометрических уравнений.
|
Уметь: решать тригонометрические уравнения.
|
|
|
|
111
112
|
Повторение. Наибольшее и наименьшее значение функции. Множество значений функции.
|
Уметь: находить наибольшее и наименьшее значение функции, множество значений функции.
|
|
|
|
113
114
|
Повторение. Решение иррациональных уравнений.
|
Уметь: решать иррациональные уравнения.
|
|
|
|
115
116
|
Повторение. Решение показательных уравнений и неравенств.
|
Уметь: решать показательные уравнения и неравенства.
|
|
|
|
117
118
|
Повторение. Решение логарифмических уравнений и неравенств.
|
Уметь: решать логарифмические уравнения и неравенства.
|
|
|
|
119
120
|
Повторение. Решение задач на проценты, движение, совместную работу.
|
Уметь: решать задачи на проценты, движение, совместную работу.
|
|
|
|
121
122
|
Повторение. Решение задач по геометрии.
|
|
|
|
|
123
124
|
Повторение. Решение задач по геометрии.
|
|
|
|
|
125
126
|
Итоговое тестирование
|
|
|
|
|
127
128
|
Решение задач ЕГЭ
|
|
|
|
|
129
130
|
Решение задач ЕГЭ
|
|
|
|
|
131
132
|
Контрольная работа
|
|
|
|
|
133
134
|
Итоговое повторение
|
|
|
|
|
 Скачать 294.05 Kb.
Скачать 294.05 Kb.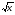 , их свойства и графики
, их свойства и графики