Методы решения нестандартных уравнений Метод разложения на множители
 Скачать 49.74 Kb. Скачать 49.74 Kb.
|
| Методы решения нестандартных уравнений 1 .Метод разложения на множители Суть этого метода заключается в следующем: уравнение f(х)*g(х)*h(х)=0 можно заменить совокупностью уравнений f(х)=0; g(х)=0; h(х)=0. Решив уравнения этой совокупности, нужно взять те их корни, которые принадлежат области определения исходного уравнения, а остальные отбросить как посторонние. Пример 1. Решить уравнение: 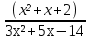 = =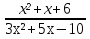 Δ Освободимся в уравнении от знаменателей дробей. При этом целесообразно суммы х²+х и 3х²+5х в левой и правой его частях считать за одно слагаемое : ((х²+х)+2)/((3х²+5х)-14)=((х²+х)+6)((3х²+5х)-10). Теперь получаем (х²+х)(3х²+5х)-10(х²+х)+2(3х²+5х)-20=(х²+х)(3х²+5х)-14(х²+х)+6(3х²+5х)-84, 4(х²+х)-4(3х²+5х)+64=0, х²+х-3х²-5х+16=0, 2х²+4х-16=0, х²+2х-8=0. Корни последнего уравнения х₁ = 2, х₂ = -4. Сделаем проверку по исходному уравнению: не обращается ли какой-либо из двух знаменателей дробей в этом уравнении в нуль? Оказывается, не обращается. Значит, это корни исходного уравнения. Ответ: 2, -4. Пример 2. Решите уравнение: 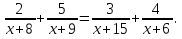 Δ Представим уравнение в таком виде: 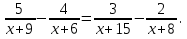 Приведем разности в левой и правой частях этого уравнения к общим знаменателям: 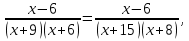 (х-6)( 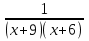 - -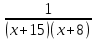 )=0. )=0.Приравняем нулю каждый из множителей в левой части последнего уравнения. Получим х – 6 =0 или 8х= 66, учитывая при этом, что х 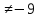 , х , х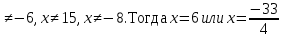 Ответ: 6,- 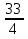 . .Пример 3.Решите уравнение: 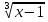 + +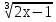 =1. =1.Δ Возведем обе части уравнения в куб. Будем иметь: х-1+2х-1+3 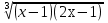 *( *(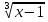 + +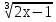 )=1, )=1,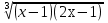 *( *(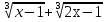 )=1-х. )=1-х.А теперь воспользуемся исходным уравнением, на основании которого сумма в скобках равна 1: 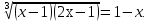 Последнее уравнение также возведем в куб: (х-1)(2х-1)=(1-х)³, (х-1)(2х-1+(х-1)²)=0, (х-1)х²=0. Отсюда х₁=1, х₂=х₃=0. Проверка по первоначальному уравнению показывает, что значение х=1 ему удовлетворяет, а значение х=0 – не удовлетворяет. Ответ: 1. 2.Метод введения новой переменной. Суть метода: если уравнение ƒ(х)=0 удалось преобразовать к виду р(q(х))=0, то нужно ввести новую переменную u=q(х), решить уравнение p(u)=0, а затем решить совокупность уравнений q(х)=u₁; q(х)=u₂…; q(х)=un, где u1, u2 …un – корни уравнения p(u)=0. Удачный выбор новой переменной делает структуру уравнения более прозрачной. Новая переменная иногда очевидна, иногда завуалирована и «проявляется» лишь в процессе преобразований. Пример 4. Решите уравнение: (х-1)(х-2)(х-4)(х-8)=4х2. ΔВ левой части уравнения умножим первый множитель на четвёртый, второй на третий, получим: (х²-6х+8)(х²-6х+8)=4х². А дальше разделим обе части уравнения на х2, пользуясь тем, что значение х=0 не является корнем уравнения: (х-9+ 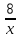 )(х-6+ )(х-6+ 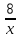 )=4. )=4.Введем подстановку: х-9+ 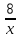 =у. Будем иметь: =у. Будем иметь:y(у+3)=4, у2+3у-4=0; у1=1, у2=-4. В обоих случаях найдем х, решая совокупность уравнений 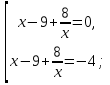 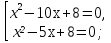 х₁,₂=5 х₁,₂=5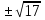 . .Ответ: 5 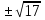 . .Пример 5.Решите уравнение: (х+3)⁴+(х+5)⁴=16. Δ Положим х+4=y ,т. к. 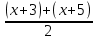 =х+4. =х+4.Имеем: (y-1)⁴+(y+1)⁴=16. Теперь нужно в левой части уравнения (y-1) и ( y+1) возвести в квадрат, а затем то, что получилось, ещё раз возвести в квадрат. После упрощений образуется биквадратное уравнение: y⁴+6y²-7=0. Его корни y₁,₂ = 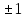 . Отсюда х₁=-3, х₂=-5. . Отсюда х₁=-3, х₂=-5.Ответ: -3, -5. Пример 6. Решите уравнение: (х²+3х-4)³+(2х²-5х+3)³=(3х²-2х-1)³. ΔВведём две подстановки: х²+3х-4=y; 2х²-5х+3= 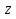 . .Получим: y³ +z³= (y + z)³ , 3yz (y + z)=0, (х²+3х-4)(2х²-5х+3)(3х²-2х-1)=0. Решая уравнения х²+3х-4=0, 2х²-5х+3=0 и 3х²-2х-1=0 найдём все корни 1, 1, 1, -4, 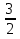 , - , - 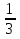 . .Ответ: 1, 1,1, -4, 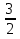 , - , - 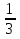 . . Пример 7. Решите уравнение: 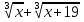 =5. =5.Δ Введем две новые переменные: 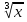 =у, =у, 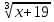 =z. =z.Получаем систему уравнений: 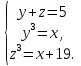 Вычтем третье из второго уравнения системы для того, чтобы исключить х: z3-у3=19. Для решения системы двух уравнений у+z=5, z3-у3=19 выразим z из первого уравнения и подставим это выражение во второе уравнение: z=5-у, (5-у)3-у3=19, 125-75у+15у2-2у3=19, 2у3-15у2+75у-106=0. Из делителей свободного члена последнему уравнению удовлетворяет у=2. Тогда уравнение приводится к виду: (у-2)(2у2-11у+51)=0. Так как дискриминант уравнения 2y² -11y+51=0 отрицателен, то других корней у уравнения нет. Следовательно, х=у3=23=8. Ответ: 8 3. Функционально-графический метод Идея графического метода решения уравнения ƒ(х)=q(х) проста и понятна: нужно построить графики функций y= ƒ(х), y = q(х) и найти точки их пересечения - корнями уравнения служат абсциссы этих точек. Этот метод позволяет определить число корней уравнения, угадать значение корня, найти приближённые , а иногда и точные значения корней. В некоторых случаях построение графиков функций можно заменить опорой на какие – либо свойства функций. Иногда знание ОДЗ позволяет доказать, что уравнение не имеет решений, а иногда позволяет найти решения уравнения непосредственной подстановкой чисел из ОДЗ. Пример 8. Решите уравнение:  + + =х³-3х+2 . =х³-3х+2 .ΔНайдём область определения D уравнения. Она совпадает с множеством всех решений системы неравенств  Решением первого неравенства является множество  , ,второго отрезок  . Следовательно, область D состоит всего из двух точек -0 и 1. Значение х=0 не удовлетворяет уравнению, значение х=1- удовлетворяет. . Следовательно, область D состоит всего из двух точек -0 и 1. Значение х=0 не удовлетворяет уравнению, значение х=1- удовлетворяет.Ответ: 1. Пример 9. Решите уравнение:  = = Δ ОДЗ этого уравнения состоит из всех х, одновременно удовлетворяющих условиям 3-х  0 и х-3 0 и х-3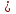 0, т. е. ОДЗ есть пустое множество. Следовательно , уравнение не имеет корней. 0, т. е. ОДЗ есть пустое множество. Следовательно , уравнение не имеет корней.Ответ: решений нет. При решении уравнений свойство ограниченности снизу или сверху функции на некотором множестве часто играет определённую роль. Например, если для всех x из некоторого множества М справедливы неравенства ƒ(х) 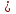 А и q(х) А и q(х)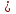 А, где А некоторое число, то на множестве М уравнение ƒ(х)=q(х) решений не имеет. А, где А некоторое число, то на множестве М уравнение ƒ(х)=q(х) решений не имеет.Пример 10. Решите уравнение: 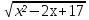 =-х²+4х. =-х²+4х.ΔСправедливы неравенства : х²-2х+17 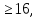 -х²+4х -х²+4х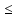 4. 4.Тогда множество значений левой части уравнения есть промежуток 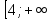 ), а правой – ( ), а правой – (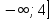 .Следовательно, равенство этих частей возможно только тогда, когда каждая из частей уравнения равна 4. Но левая часть равна 4 прих=1, а правая – при х=2. Это значит, что уравнение не имеет решений. .Следовательно, равенство этих частей возможно только тогда, когда каждая из частей уравнения равна 4. Но левая часть равна 4 прих=1, а правая – при х=2. Это значит, что уравнение не имеет решений.Ответ: решений нет. Пример 11. Решите уравнение: 10х⁴+3х³+5х²+5х+8=0. ΔСделаем уравнение приведённым: х⁴+ 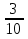 х³+ х³+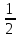 х²+ х²+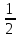 х+ х+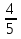 =0. =0.Дополним сумму х⁴ + 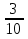 х³ до квадрата суммы: х³ до квадрата суммы:(х² + 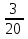 х)² +( х)² +(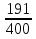 х²+ х²+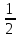 х + х +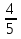 )=0. )=0.Дискриминант квадратного трёхчлена, стоящего во вторых скобках , отрицателен, поэтому трёхчлен при х сохраняет постоянный знак, а именно положительный. Но тогда вся левая часть уравнения положительна; следовательно, уравнение не имеет решений. Ответ: решений нет. Пример 12. Решите уравнение: 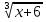 + +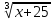 +х=7. +х=7.Δ Очевидно один корень уравнения – х=2. Имеет ли оно другие корни? Левая часть уравнения есть возрастающая функция, как сумма трех возрастающих функций. Но монотонная функция каждое свое значение (в данном случае значение 7) принимает в единственной точке, поэтому других корней у уравнения нет Ответ: 2. |