Протокол № от 2015 г. «Согласовано»
 Скачать 475.34 Kb. Скачать 475.34 Kb.
|
| Департамент образования города Москвы Государственное бюджетное общеобразовательное учреждение города Москвы «Школа № 498» Структурное подразделение № 622
РАБОЧАЯ ПРОГРАММА ПО УЧЕБНОМУ КУРСУ «МАТЕМАТИКА» 8 «И» КЛАСС НА 2015-2016 УЧЕБНЫЙ ГОД Составила Бобовникова О.Г., учитель математики МОСКВА 2015. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Рабочая программа составлена на основе Примерной программы основного общего образо вания по математике:
Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и дает примерное распределение учебных часов по разделам курса. Выполняет две основные функции. Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета. Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся. В настоящей рабочей программе на изучение алгебры предусмотрено 4 часа в неделю, всего 136 часов, на изучение геометрии – 2 часа в неделю, всего 68 часов в год. Общеучебные умения, навыки и способы деятельности. В ходе преподавания математики в основной школе, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
В ходе освоения содержания курса учащиеся получают возможность:
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
Основные развивающие и воспитательные цели Развитие:
Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов. Воспитание:
Основные цели курса алгебры: -овладение математическими знаниями, необходимыми для изучения физики, химии и для продолжения образования; -развитие интереса к алгебре, формирование любознательности; -развитие индивидуальных способностей, творческой активности, умения выбирать пути решения задач; -подведение к пониманию значимости математики в развитии общества. Задачи обучения: -развитие и углубление вычислительных навыков и умений до уровня, позволяющего уверенно применять знания при решении задач математики, физики и химии: -ввести понятие функции и научить правильно применять знания о функции в старших классах; -систематизировать и обобщить сведения о преобразовании выражений, решении линейных уравнений; -изучить формулы умножения и научить уверенно, применять эти формулы при преобразовании выражений и решении уравнений; -научить решать системы уравнений и текстовые задачи с помощью систем; -ввести понятие степени с натуральным показателем и научить упрощать выражения со степенями, находить значения выражений со степенями. -изучить начальный курс статистики и теории вероятностей. СОДЕРЖАНИЕ ОБУЧЕНИЯ (АЛГЕБРА) 1.Рациональные дроби и их свойства (23 часа). Рациональная дробь. Основное свойство дроби, сокращение дробей. Сложение, вычитание, умножение и деление дробей. Преобразования рациональных выражений. Функция у = к/х и ее график. Основная цель - выработать умение выполнять тождественные преобразования рациональных выражений. Знать: - основное свойство дроби; - знать правила сложения и вычитания дробей с одинаковыми и разными знаменателями; - знать правила умножения и деления дробей. Уметь: -уметь находить допустимые значения переменной; -уметь сокращать дроби после разложения на множители числителя и знаменателя; - выполнять действия с алгебраическими дробями; - упрощать выражения с алгебраическими дробями; -строить график обратно пропорциональной функции и работать с ним. 2.Квадратные корни (18 часов). Понятие об иррациональном числе. Общие сведения о действительных числах. Квадратный корень, приближенное значение квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция у = 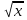 , ее свойства и график. , ее свойства и график. Основная цель - систематизировать сведения о рациональных числах и дать представление об иррациональных числах и дать представление об иррациональных числах, расширив тем самым понятие числа; выработать умение выполнять простейшие преобразования выражений, содержащих квадратные корни. Знать: - определение арифметического квадратного корня; - свойства арифметического квадратного корня. Уметь: - применять свойства арифметического квадратного корня к преобразованию выражений; - вычислять значения выражений, содержащих квадратные корни; - исследовать уравнение 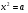 ; ;- строить график функции 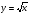 и работать с ним. и работать с ним.3.Квадратные уравнения (26 часов). Квадратное уравнение. Формулы корней квадратного уравнения. Теорема Виета. Решение рациональных уравнений. Решение задач, приводящих к квадратным и рациональным уравнениям. Основная цель - выработать умения решать квадратные уравнения, простейшие рациональные уравнения и применять их к решению задач. Распознавать квадратные и дробные уравнения. Знать: - способы решения неполных квадратных уравнений; - формулу корней квадратного уравнения. Уметь: - решать квадратные уравнения, а также уравнения сводящиеся к ним; - решать дробно-рациональные уравнения; - исследовать квадратное уравнение по дискриминанту и коэффициентам; - решать текстовые задачи с помощью квадратных и дробно-рациональных уравнений. 4.Неравенства (18 часов). Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Применение свойств неравенств к оценке значения выражения. Линейное неравенство с одной переменной. Система линейных неравенств с одной переменной. Основная цель - выработать умение решать линейные неравенства с одной переменной и их системы. Знать: - определение числового неравенства - свойства числовых неравенств; - что значит решить систему неравенств. Уметь: - находить пересечение и объединение множеств; - иллюстрировать на координатной прямой числовые неравенства; - применять свойства числовых неравенств при решении задач; - решать линейные неравенства; - решать системы неравенств с одной переменной. 5.Теория вероятностей и статистика (17 часов). Знать: а) основные понятия и определения по теории вероятностей и статистике по программе; б) формулы нахождения вероятности события, сложения и умножения вероятностей; Уметь: а) уверенно искать нужную информацию в таблице; б) выполнять элементарные вычисления по табличным данным; в) строить столбиковые и круговые диаграммы по имеющимся данным; г) объяснять и вычислять медиану, среднее арифметическое, размах и дисперсию для набора чисел; д) приводить примеры случайных событий и случайной изменчивости; д) владеть алгоритмами решения основных задач; е) пользоваться статистическим языком для описания предметов окружающего мира. 6. Степень с целым показателем (16 часов). Степень с целым показателем и ее свойства. Стандартный вид числа. Запись приближенных значений. (Действия над приближенными значениями). Основная цель - сформировать умение выполнять действия над степенями с целыми показателями, ввести понятие стандартного вида числа. Знать: - определение степени с целым показателем; - свойства степени с целым показателем; Уметь: - выполнять вычисления с числами, записанными в стандартном виде; - применять свойства степени с целым показателем для преобразования выражений и вычислений; - строить гистограммы. 7.Итоговое повторение (18 часов). Повторение основных вопросов курса. Решение примеров и задач по основным темам. Основная цель - обобщение и систематизация изученного материала, отработка основных навыков и умений. В результате изучения курса алгебры восьмого класса учащиеся должны: -правильно употреблять термины, связанные с различными видами чисел и способами их записи; -выполнять действия со степенями с целым показателем; - выполнять преобразования числовых выражений, содержащих квадратные корни; -решать квадратные уравнения; - правильно употреблять термины «уравнение», «неравенство», «система», «корень уравнения», «решение системы», понимать их в тексте и речи учителя, формулировку задачи « решить уравнение, неравенство, систему»; -решать линейные неравенства с одной переменной и их системы; -решать текстовые задачи с помощью составления уравнений; -строить графики функции у = х2 и у = х3; -выполнять действия над приближенными значениями. СОДЕРЖАНИЕ ОБУЧЕНИЯ (ГЕОМЕТРИЯ) 1.Четырехугольники (12 часов). Многоугольник, выпуклый многоугольник, четырехуголь ник. Параллелограмм, его свойства и признаки. Трапеция. Пря моугольник, ромб, квадрат, их свойства. Осевая и центральная симметрии. Цель: изучить наиболее важные виды четы рехугольников — параллелограмм, прямоугольник, ромб, квад рат, трапецию; дать представление о фигурах, обладающих осе вой или центральной симметрией. Доказательства большинства теорем данной темы и решения многих задач проводятся с помощью признаков равенства треугольников, поэтому полезно их повторить, в начале изучения темы. Осевая и центральная симметрии вводятся не как преобразо вание плоскости, а как свойства геометрических фигур, в част ности четырехугольников. Рассмотрение этих понятий как дви жений плоскости состоится в 9 классе. Знать: - Определения: многоугольника, параллелограмма, трапеции, прямоугольника, ромба, квадрата; - формулу суммы углов выпуклого многоугольника; - свойства этих четырехугольников; - признаки параллелограмма; - виды симметрии. Уметь: - распознавать на чертеже многоугольники и выпуклые многоугольники; параллелограммы и трапеции; - применять формулу суммы углов выпуклого многоугольника; - применять свойства и признаки параллелограммов при решении задач; - делить отрезок на n равных частей; - строить симметричные точки и распознавать фигуры, обладающие осевой и центральной симметрией; - выполнять чертеж по условию задачи 2.Площадь (13 часов). Понятие площади многоугольника. Площади прямоуголь ника, параллелограмма, треугольника, трапеции. Теорема Пи фагора. Цель: расширить и углубить полученные в 5—6 классах представления обучающихся об измерении и вычисле нии площадей; вывести формулы площадей прямоугольника, па раллелограмма, треугольника, трапеции; доказать одну из глав ных теорем геометрии — теорему Пифагора. Вывод формул для вычисления площадей прямоугольника, параллелограмма, треугольника, трапеции основывается на двух основных свойствах площадей, которые принимаются исходя из наглядных представлений, а также на формуле площади квад рата, обоснование которой не является обязательным для обучающихся. Нетрадиционной для школьного курса является теорема об от ношении площадей треугольников, имеющих по равному углу. Она позволяет в дальнейшем дать простое доказательство призна ков подобия треугольников. В этом состоит одно из преимуществ, обусловленных ранним введением понятия площади. Доказательство теоремы Пифагора основывается на свойствах площадей и формулах для площадей квадрата и прямоугольника. Доказывается также теорема, обратная теореме Пифагора. Знать: - представление о способе измерения площади, свойства площадей; - формулы площадей: прямоугольника, параллелограмма, треугольника, трапеции; - формулировку теоремы Пифагора и обратной ей. Уметь: - находить площади прямоугольника, параллелограмма, треугольника, трапеции; - применять формулы при решении задач; - находить стороны треугольника, используя теорему Пифагора; - определять вид треугольника, используя теорему, обратную теореме Пифагора. - выполнять чертеж по условию задачи. 3.Подобные треугольники (17 часов). Подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательству теорем и решению задач. Синус, косинус и тангенс острого угла прямоугольного треуголь ника. Цель: ввести понятие подобных треугольни ков; рассмотреть признаки подобия треугольников и их применения; сделать первый шаг в освоении учащимися тригонометриче ского аппарата геометрии. Определение подобных треугольников дается не на основе преобразования подобия, а через равенство углов и пропорцио нальность сходственных сторон. Признаки подобия треугольников доказываются с помощью теоремы об отношении площадей треугольников, имеющих по равному углу. На основе признаков подобия доказывается теорема о средней линии треугольника, утверждение о точке пересечения медиан треугольника, а также два утверждения о пропорциональных отрезках в прямоугольном треугольнике. Дается представление о методе подобия в задачах на построение. В заключение темы вводятся элементы тригонометрии — синус, косинус и тангенс острого угла прямоугольного треугольника. Знать: - определение подобных треугольников; - формулировки признаков подобия треугольников; - формулировку теоремы об отношении площадей подобных треугольников; - формулировку теоремы о средней линии треугольника; - свойство медиан треугольника; -понятие среднего пропорционального, - свойство высоты прямоугольного треугольника, проведенной из вершины прямого угла; - определение синуса, косинуса, тангенса острого угла прямоугольного треугольника - значения синуса, косинуса, тангенса углов 30º, 45º, 60º, 90º. Уметь: - находить элементы треугольников, используя определение подобных треугольников; - находить отношение площадей подобных треугольников; - применять признаки подобия при решении задач; - применять метод подобия при решении задач на построение; - находить значение одной из тригонометрических функций по значению другой; - решать прямоугольные треугольники. 4.Окружность (14 часов). Взаимное расположение прямой и окружности. Касательная к окружности, ее свойство и признак. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности. Цель: расширить сведения об окружности, полученные учащимися в 7 классе; изучить новые факты, связанные с окружностью; познакомить обучающихся с четырьмя заме чательными точками треугольника. В данной теме вводится много новых понятий и рассматривается много утверждений, связанных с окружностью. Для их усвоения следует уделить большое внимание решению задач. Утверждения о точке пересечения биссектрис треугольника и точке пересечения серединных перпендикуляров к сторонам треугольника выводятся как следствия из теорем о свойствах биссектрисы угла и серединного перпендикуляра к отрезку. Теорема о точке пересечения высот треугольника (или их продолжений) доказывается с помощью утверждения о точке пересечения серединных перпендикуляров. Наряду с теоремами об окружностях, вписанной в треуголь ник и описанной около него, рассматриваются свойство сторон описанного четырехугольника и свойство углов вписанного че тырехугольника. Знать: - случаи взаимного расположения прямой и окружности; - понятие касательной, точек касания, свойство касательной; - определение вписанного и центрального углов; - определение серединного перпендикуляра; - формулировку теоремы об отрезках пересекающихся хорд; - четыре замечательные точки треугольника; - определение вписанной и описанной окружностей. Уметь: - определять и изображать взаимное расположение прямой и окружности; - окружности, вписанные в многоугольник и описанные около него; - распознавать и изображать центральные и вписанные углы; - находить величину центрального и вписанного углов; - применять свойства вписанного и описанного четырехугольника при решении задач; - выполнять чертеж по условию задачи; - решать простейшие задачи, опираясь на изученные свойства. 5. Повторение (3 часа) Цели изучения курса геометрии в 8 классе:
Задачи изучения курса геометрии в 8 классе:
В курсе геометрии 8-го класса продолжается решение задач на признаки равенства треугольников, но в совокупности с применением новых теоретических фактов. Теорема о сумме углов выпуклого многоугольника позволяет расширить класс задач. Формируются практические навыки вычисления площадей многоугольников в ходе решения задач. Особое внимание уделяется применению подобия треугольников к доказательствам теорем и решению задач. Вводятся первые знания о синусе, косинусе и тангенсе острого угла прямоугольного треугольника. Систематизируются сведения об окружности и её свойствах, вписанной и описанной окружностях. Серьезное внимание уделяется формированию умений рассуждать, выполнять простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов. Результаты обучения Результаты обучения представлены в «Требованиях к уровню подготовки», задающих систему итоговых результатов обучения, которые должны быть достигнуты всеми учащимися, оканчивающими 8 класс, и достижение которых является обязательным условием положительной аттестации ученика за курс 8 класса. Эти требования структурированы по трем компонентам: «знать/понимать», «уметь», «использовать приобретенные знания и умения в практической деятельности и повседневной жизни». Требования к уровню подготовки. В результате изучения курса геометрии 8 класса обучающиеся должны: Знать:
уметь:
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Общеучебные умения, навыки и способы деятельности. В ходе преподавания геометрии в 8 классе, работы над формированием у обучающихся перечисленных в программе знаний и умений следует обращать внимание на то, чтобы они овладевали овла девали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
Планирование учебного материала по алгебре 8 класс. 4 ч в неделю,всего 136 ч. в год. Учебники: Алгебра 8, Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова, под ред. С.А.Теляковского «Просвещение», 2010 год.
|