Протокол № От 2014 г. /В. В. Симутина/ Согласовано
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
| III. СОДЕРЖАНИЕ ТЕМ УЧЕБНОГО КУРСА «МАТЕМАТИКА» Модуль «алгебра»
Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума. Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях. Преобразования графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой 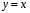 , растяжение и сжатие вдоль осей координат. , растяжение и сжатие вдоль осей координат. 2.Предел функции и непрерывность (5 часов) Понятие о непрерывности функции. Основные теоремы о непрерывных функциях. Понятие о пределе функции в точке. Поведение функций на бесконечности. Асимптоты. Вертикальные и горизонтальные асимптоты графиков. Графики дробно-линейных функций. 3.Обратные функции (5 часов) Сложная функция (композиция функций). Взаимно обратные функции. Область определения и область значений обратной функции. График обратной функции. Нахождение функции, обратной данной. Обратные тригонометрические функции, их свойства и графики. 4.Производная (11 часов). Понятие о производной функции, физический и геометрический смысл производной. Уравнение касательной к графику функции. Производные суммы, разности, произведения и частного. Производные основных элементарных функций. Производные сложной и обратной функций. 5.Применение производной (15 часов) Вторая производная. Применение производной к исследованию функций и построению графиков. Использование производных при решении уравнений и неравенств, при решении текстовых, физических и геометрических задач, нахождении наибольших и наименьших значений. Примеры использования производной для нахождения наилучшего решения в прикладных задачах. Нахождение скорости для процесса, заданного формулой или графиком. Примеры применения интеграла в физике и геометрии. Вторая производная и ее физический смысл. 6.Первообразная и интеграл (13 часов). Площадь криволинейной трапеции. Понятие об определенном интеграле. Первообразная. Первообразные элементарных функций. Правила вычисления первообразных. Формула Ньютона-Лейбница.Примеры применения интеграла в физике и геометрии. 7.Уравнения-следствия (9 часов) Понятие уравнения-следствия. Возведение уравнения в четвертую степень. Потенцирование уравнений. Применение нескольких преобразований, приводящих к уравнению-следствию. 8.Равносильность уравнений на множествах (12 часов) Возведение уравнения в натуральную степень. Потенцирование и логарифмирование уравнений. Умножение уравнения на функцию. Применение нескольких преобразований. Уравнения с дополнительными условиями.
Возведение неравенств в натуральную степень. Потенцирование и логарифмирование неравенств. Умножение неравенства на функцию. Применение нескольких преобразований. Неравенства с дополнительными условиями. Нестрогие неравенства.
Уравнения с модулями. Неравенства с модулями. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств.
Многочлены от двух переменных. Многочлены от нескольких переменных, симметрические Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность уравнений, неравенств, систем. . Решение иррациональных неравенств. Решение систем уравнений с двумя неизвестными простейших типов. Решение систем неравенств с одной переменной. Доказательства неравенств. Неравенство о среднем арифметическом и среднем геометрическом двух чисел. Переход к пределам в неравенствах. Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем. 12.Нестандартные методы решения уравнений и неравенств (6 часов) Использование областей существования функций. Использование неотрицательности и ограниченности функции. Использование свойств синуса и косинуса, числовых неравенств, производной для решения уравнений и неравенств. 13.Системы уравнений с несколькими неизвестными (7 часов) Равносильность систем. Система-следствие. Метод замены неизвестныж. Нестандартные методы решения уравнений и неравенств. 14.Уравнения и неравенства с параметрами (4 часа) Уравнения и неравенства с параметром. Системы уравнений с параметром. Задачи с условиями. Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений. 15 Комплексные числа (8 часов) Комплексные числа. Геометрическая интерпретация комплексных чисел. Действительная и мнимая часть, модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы записи комплексных чисел. Арифметические действия над комплексными числами в разных формах записи. Комплексно сопряженные числа. Возведение в натуральную степень (формула Муавра). Основная теорема алгебры. 16.Повторение курса алгебры и математического анализа Уравнения и неравенства с параметром., функции и графики. Решение уравнений: рациональных, иррациональных, показательных, логарифмических, тригонометрических. Модуль «геометрия» 1. Многогранники (19 часов) Двугранный угол, линейный угол двугранного угла. Многогранные углы. Вершины, ребра, грани многогранника. Призма, ее основания, боковые ребра, высота, боковая поверхность. Построение сечений. Прямая и наклонная призма. Правильная призма. Параллелепипед. Пирамида, ее основание, боковые ребра, высота, боковая поверхность. Построение сечений. Усеченная пирамида. Правильная пирамида. Правильные многогранники. 2. Тела вращения (14 часов) Цилиндр. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения параллельные основанию. Конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения параллельные основанию. Шар и сфера, их сечения. Касательная плоскость к сфере. Сфера, вписанная в многогранник, сфера, описанная около многогранника. 3. Объемы многогранников (10 часов) Понятие об объеме тела. Формулы объема параллелепипеда, призмы. Формулы объема пирамиды. Отношение объемов подобных тел. 4. Объемы и поверхности тел вращения (12 часов) Формулы объема цилиндра и конуса. Формулы объема шара. Формулы площади поверхностей цилиндра и конуса. Формулы площади сферы. 5. Повторение Призма. Прямая и наклонная призма. Правильная призма. Параллелепипед. Пирамида. Цилиндр. Конус. Шар и сфера. Формулы объема куба, параллелепипеда, призмы, цилиндра. Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса. Формулы объема шара и площади сферы. IV КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ ( смотреть в приложении) IV КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ (6 ч в неделю, всего 210 ч)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||