Протокол № от 2013г. «Согласовано» Заместитель руководителя по увр мбоу сош №46
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
| Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа № 46
РАБОЧАЯ ПРОГРАММА ПЕДАГОГА Ильюшко Марина Михайловна, 2 категория Ф.И.О., категория по алгебре 9 класс предмет, класс Рассмотрено на заседании педагогического совета протокол № ___________ от «____» __________ 2013г. 2013-2014 учебный год Пояснительная записка Рабочая программа по алгебре для 9 класса составлена на основе федерального компонента государственного стандарта основного общего образования. Данная рабочая программа ориентирована на учащихся 9 класса и реализуется на основе следующих документов: 1. . Программы общеобразовательных учреждений. Алгебра 7-9 классы / Сост. Т.А. Бурмистрова - Москва: «Просвещение», 2009. Программа по алгебре 9 класс, автор С.М. Никольский. 2. Стандарт основного общего образования по математике. Стандарт основного общего образования по математике //Сборник нормативно- правовых документов и методических материалов, Москва: «Вентана- Граф», 2008. Она разработана в целях конкретизации содержания образовательного стандарта по математике с учётом межпредметных и внутрипредметных связей, логики учебного процесса и возрастных особенностей школьников. В программе дается распределение учебных часов по крупным разделам курса. Цели обучения математики в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека. Алгебра нацелена на формирование математического аппарата для решения задач из математики и смежных предметов (физика, химия, основы информатики и вычислительной техники и др.). В задачи обучения математики входит:
Курс алгебры построен в соответствии с традиционными содержательно-методическими линиями: числовой, функциональной, алгоритмической, уравнений и неравенств, алгебраических преобразований. Согласно базисному учебному плану для образовательного учреждения на изучение алгебры 9 класса отводится 4 часа в неделю. Программа рассчитана на 136 ч. СОДЕРЖАНИЕ ОБУЧЕНИЯ 1. Линейные неравенства с одним неизвестным (13ч) Неравенства первой степени с одним неизвестным. Линейные неравенства с одним неизвестным. Системы линейных неравенств с одним неизвестным. Основная цель — выработать умение решать неравенства первой степени с одним неизвестным, линейные неравенства и системы линейных неравенств. В данной теме вводится понятие неравенства первой степени с одним неизвестным (кх + Ъ > 0, кх + Ъ < О, к ≠ 0). Решение таких неравенств основывается на свойствах числовых неравенств и иллюстрируется с помощью графиков линейных функций. Вводятся понятия линейного неравенства, системы линейных неравенств и рассматриваются приемы их решения. 2. Неравенства второй степени с одним неизвестным (14ч) Неравенства второй степени с одним неизвестным. Неравенства, сводящиеся к неравенствам второй степени. Основная цель — выработать умение решать неравенства второй' степени с одним неизвестным. Вводятся понятия неравенства второй степени с одним неизвестным и его дискриминанта D, последовательно рассматриваются случаи D>0, D = 0, D < 0. Решение неравенств основано на определении знака квадратного трехчлена на интервалах и иллюстрируется схематическим построением графиков квадратичных функций. 3. Рациональные неравенства (17ч) Метод интервалов. Решение рациональных неравенств. Системы рациональных неравенств. Нестрогие рациональные неравенства. Основная цель — выработать умение решать рациональные неравенства и их системы, нестрогие неравенства. При решении рациональных неравенств используется метод интервалов, который, по сути, применялся уже при решении квадратных неравенств. Показывается равносильность неравенства вида 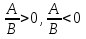 неравенствам неравенствам 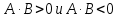 соответственно (А и В — многочлены). соответственно (А и В — многочлены).После изучения строгих неравенств: линейных, квадратных, рациональных — рассматриваются нестрогие неравенства всех ранее изученных типов и их системы. Решение нестрогих неравенств должно состоять из трех этапов: 1) решить уравнение; 2) решить строгое неравенство; 3) объединить решения уравнения и строгого неравенства. Попытка отойти от этого правила часто приводит к ошибкам. 4. Корень n- й степени (18ч) Свойства функции у = хп и ее график. Корень п-й степени. Корни четной и нечетной степени. Арифметический корень. Свойства корней п-й степени. Корень п-й степени из натурального числа. Функция 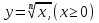 . [Степень с рациональным показателем и ее свойства. . [Степень с рациональным показателем и ее свойства.Основная цель — изучить свойства функций у = хп и 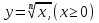 их графики, свойства корня п-й степени; выработать умение преобразовывать выражения, содержащие корни п-й степени. их графики, свойства корня п-й степени; выработать умение преобразовывать выражения, содержащие корни п-й степени.В данной теме рассматриваются понятие и свойства корня п-й степени. Но от учащихся требуется знание лишь корней второй и третьей степени и их свойств. 5. Числовые последовательности, арифметическая и геометрическая прогрессии(2+7+8=17ч) Числовая последовательность. [Свойства числовых последовательностей.] Арифметическая и геометрическая прогрессии. Формулы суммы п первых членов арифметической и геометрической прогрессий. Бесконечно убывающая геометрическая прогрессия. [Принцип полной индукции.] Основная цель — выработать умения, связанные с задачами на арифметическую и геометрическую прогрессии. В данной теме вводятся понятия числовой последовательности, арифметической и геометрической прогрессий, решаются традиционные задачи, связанные с формулами п-го члена и суммы п первых членов арифметической и геометрической прогрессий. 6.Тригонометрические формулы (15 ч) Понятие угла. Определение синуса и косинуса угла. Основные формулы для 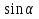 и и 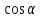 . Тангенс и котангенс угла. . Тангенс и котангенс угла.Основная цель — усвоить понятия синуса, косинуса, тангенса и котангенса произвольного угла, выработать умения по значению одной из этих величин находить другие и выполнять тождественные преобразования простейших тригонометрических выражений. Данная тема курса алгебры опирается на определения и некоторые факты из курса геометрии. Все тригонометрические формулы следует привести с доказательством, не используя термины «тригонометрические функции» и «формулы приведения». 7. Приближения чисел (17ч) Абсолютная и относительная погрешности приближения. [Приближения суммы и разности, произведения и частного двух чисел, суммы нескольких слагаемых. Приближенные вычисления с калькулятором.] Основная цель — усвоить понятия абсолютной и относительной погрешностей приближения, выработать умение выполнять оценку результатов вычислений. В данной теме вводятся понятия абсолютной и относительной погрешностей приближения, показываются приемы оценки результатов вычислений при сложении, вычитании, умножении, делении. Элементы комбинаторики и теории вероятности. Примеры комбинаторных задач, перестановки, размещения. Основная цель – дать понятия комбинаторики, перестановки, размещения, научить решать связанные с ними задачи. 8. Итоговое повторение (6+19=25ч) Основная цель: повторить курс алгебры 7-9 класса; подготовить к ГИА |