|
Протокол № от 200 г. «Согласовано» на мс школы Заместитель руководителя по увр моу сош №3
Муниципальное общеобразовательное учреждение
средняя общеобразовательная школа №3 г. Вязьмы Смоленской области
«Рассмотрено» на заседании ШМО учителей математики
Руководитель МО
___________/______________/
ФИО
Протокол № ____ от «___»________200___г.
|
«Согласовано» на МС школы
Заместитель руководителя по УВР МОУ СОШ №3
_____________/В.А.Зеленцова/
ФИО
«___»___________200___г.
|
«Утверждаю»
Директор МОУ СОШ №3 г.Вязьмы
_____________/Н.А.Венедиктова/
ФИО
Приказ №_____от «__»________200___г.
|
РАБОЧАЯ ПРОГРАММА
по математике
10 Б класс по учебникам А.Г. Мордковича и Л.С. Атанасяна
учителя высшей категории Малышевой И.Н.
2011 – 2012 учебный год
Классы 10Б
Учитель _Малышева И.Н.
Количество часов
Всего 204 часа; в неделю _6_час.
Плановых контрольных уроков __13
Планирование составлено на основе сборника нормативных документов Математика /Сост. Э.Д.Днепров, А.Г.Аркадьев – 2е изд. –М.:Дрофа-2007 г.
Программы. Математика. 5-6 классы. Алгебра. 7-9 классы. Алгебра и начала анализа. 10 – 11 классы/ авт.-сост. И. И.Зубарева, А. Г. Мордкович.- М.: Мнемозина, 2007.
Учебник: Алгебра и начала математического анализа профильный уровень 10-11 кл. А.Г. Мордкович, П.В.Семенов. В двух частях. ч.1: Учеб. для общеобраз. учреждений. – 3-е изд. испр. М.: Мнемозина, 2010. ч.2. Задачник.
Программы общеобразовательных учреждений. Геометрия. 10-11 классы. Сост. Бурмистрова Т.А.-М.: Просвещение, 2008г.
Учебник: Геометрия 10-11 класс Учеб. для общеобраз. учреждений. Базовой и профильный уровни Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. –М. Просвещение, 2010г.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Настоящая программа по математике для 10 класса (профильный уровень) составлена на основе Федерального компонента государственного стандарта среднего образования (сборник нормативных документов Математика /Сост. Э.Д.Днепров, А.Г.Аркадьев – 2е изд. –М.:Дрофа-2007 г.), примерной программы для общеобразовательных учреждений по алгебре и началам математического анализа к УМК «Алгебра - 10 класс. Профильный уровень - автор А.Г.Мордкович» [Программы для общеобразовательных учреждений. Алгебра и начала математического анализа. 10-11 классы. Авторы-составители И.И.Зубарева, А.Г.Мордкович – М.: Мнемозина, 2007.] и примерной программы общеобразовательных учреждений. Геометрия. 10-11 классы. Сост. Бурмистрова Т.А.-М.: Просвещение, 2008г.
В профильном курсе содержание образования, представленное в основной школе, развивается в следующих направлениях:
• систематизация сведений о числах; формирование представлений о расширении числовых множеств от натуральных до комплексных как способе построения нового математического аппарата для решения задач окружающего мира и внутренних задач математики; совершенствование техники вычислений;
• развитие и совершенствование техники алгебраических преобразований, решения уравнений, неравенств, систем;
• систематизация и расширение сведений о функциях, совершенствование графических умений; знакомство с основными идеями и методами математического анализа в объеме, позволяющем исследовать элементарные функции и решать простейшие геометрические, физические и другие задачи;
• расширение системы сведений о свойствах плоских фигур, систематическое изучение свойств пространственных тел, развитие представлений о геометрических измерениях;
• развитие представлений о вероятностно-статистических закономерностях в окружающем мире;
• совершенствование математического развития до уровня, позволяющего свободно применять изученные факты и методы при решении задач из различных разделов курса, а также использовать их в нестандартных ситуациях;
• формирование способности строить и исследовать простейшие математические модели при решении прикладных задач, задач из смежных дисциплин, углубление знаний об особенностях применения математических методов к исследованию процессов и явлений в природе и обществе.
В рабочей программе представлены содержание математического образования, требования к обязательному уровню подготовки обучающегося, критерии и нормы оценки знаний, умений и навыков обучающихся, виды контроля, ресурсное обеспечение программы (литература), тематическое планирование уроков математики.
В соответствие с федеральным базисным учебным планом на изучение математики на профильном уровне в 10 классе отводится 6 часов в неделю.
Курс математики 10 класса состоит из следующих предметов: «Алгебра и начала анализа», «Геометрия», «Элементы логики, комбинаторики, статистики и теории вероятности», которые изучаются блоками. Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и показывает распределение учебных часов по разделам курса. Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение алгебры и началам математического анализа в 10 (профильный уровень) классе отводится 136 часов из расчёта 4 часа в неделю, на изучение геометрии в 10 классе отводится 68 часов из расчёта 2 часа в неделю. Рабочая программа по математике для 10Б класса рассчитана на это же количество часов. Всего 204 часа, 6 часов в неделю. В соответствии с этим составлено тематическое планирование на 204 урока.
Цели изучения математики:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование умений точно, грамотно, аргументировано излагать мысли как в устной, так и в письменной форме, овладение методами поиска, систематизации, анализа, классификации информации из различных источников (включая учебную, справочную литературу, современные информационные технологии);
формирование представлений об идеях и методах математики как средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Отличительных особенностей рабочей программы по сравнению с примерной нет.
Срок реализации рабочей учебной программы – один учебный год.
В данном классе ведущими методами обучения предмету являются: поисковый, объяснительно-иллюстративный и репродуктивный. На уроках используются элементы следующих технологий: личностно ориентированное обучение, обучение с применением опорных схем, ИКТ.
Уровень обучения: профильный.
Формы промежуточной и итоговой аттестации.
Промежуточная аттестация проводится в форме контрольных, самостоятельных и зачетных работ, математических диктантов. Итоговая аттестация предусмотрена в виде двухчасовой итоговой контрольной работы.
Содержание программы
Алгебры и начала математического анализа
Повторение материала 7-9 классов (3ч)
Действительные числа (12ч)
Натуральные и целые числа. Делимость чисел. Основная теорема арифметики натуральных чисел. Рациональные, иррациональные, действительные числа, числовая прямая. Числовые неравенства. Аксиоматика действительных чисел. Модуль действительного числа. Метод математической индукции.
Числовые функции (10ч)
Определение числовой функции, способы ее задания, свойства функций. Периодические и обратные функции.
Тригонометрические функции (24ч)
Числовая окружность на координатной плоскости. Синус и косинус. Тангенс и котангенс. Тригонометрические функции числового аргумента. Тригонометрические функции углового аргумента, их свойства и графики. Сжатие и растяжение графиков тригонометрических функций. Обратные тригонометрические функции.
Тригонометрические уравнения и неравенства (10ч)
Простейшие тригонометрические уравнения и неравенства. Методы решения тригонометрических уравнений: введение новой переменной, разложение на множители, однородные тригонометрические уравнения.
Преобразование тригонометрических выражений (21ч)
Формулы сложения, приведения, двойного аргумента, понижения степени. Преобразование суммы тригонометрических функций в произведение. Преобразование произведений тригонометрических функций в суммы. Методы решения тригонометрических уравнений (продолжение).
Комплексные числа (9ч)
Комплексные числа и арифметические операции над ними. Комплексные числа и координатная плоскость. Тригонометрическая форма записи комплексного числа. Комплексные числа и квадратные уравнения. Возведение комплексного числа в степень. Извлечение квадратного и кубического корня из комплексного числа.
Производная (29ч)
Определение числовой последовательности и способы ее задания. Свойства числовых последовательностей.
Определение предела последовательности. Свойства сходящихся последовательностей. Вычисление пределов последовательностей. Сумма бесконечной геометрической прогрессии.
Предел функции на бесконечности. Предел функции в точке. Приращение аргумента. Приращение функции.
Задачи, приводящие к понятию производной. Определение производной. Алгоритм отыскания производной. Формулы дифференцирования. Правила дифференцирования. Понятие производной n-го порядка. Дифференцирование сложной функции. Дифференцирование обратной функции. Уравнение касательной к графику функции. Алгоритм составления уравнения касательной к графику функции y = f(x).
Применение производной для доказательства тождеств и неравенств. Построение графиков функций. Применение производной для отыскания наибольших и наименьших значений непрерывной функции на промежутке. Задачи на оптимизацию.
Комбинаторика и вероятность (8ч).
Правило умножения. Перестановки и факториалы. Выбор нескольких элементов. Сочетания и размещения. Бином Ньютона. Случайные события и их вероятности.
Геометрия
Введение (6ч).
Предмет стереометрии. Аксиомы стереометрии. Некоторые следствия из аксиом.
Основная цель – познакомить учащихся с содержанием курса стереометрии, с основными понятиями и аксиомами, принятыми в данном курсе, вывести первые следствия из аксиом, дать представление о геометрических телах и их поверхностях, об изображении пространственных фигур на чертеже, о прикладном значении геометрии.
Параллельность прямых и плоскостей (20ч).
Параллельность прямых, прямой и плоскости. Взаимное расположение двух прямых в пространстве. Угол между двумя прямыми. Параллельность плоскостей. Тетраэдр и параллелепипед.
Основная цель – сформировать представления учащихся о возможных случаях взаимного расположения двух прямых в пространстве, прямой и плоскости, изучить свойства и признаки параллельности прямых и плоскостей.
Перпендикулярность прямых и плоскостей (20ч).
Перпендикулярность прямой и плоскости. Перпендикуляр и наклонные. Угол между прямой и плоскостью. Двугранный угол. Перпендикулярность плоскостей. Трехгранный угол. Многогранный угол. Перпендикулярность плоскостей.
Основная цель – ввести понятия перпендикулярности прямых и плоскостей, изучить признаки перпендикулярности прямой и плоскости, двух плоскостей.
Многогранники (14ч).
Понятие многогранника. Геометрическое тело. Теорема Эйлера. Призма. Пространственная теорема Пифагора. Пирамида. Правильные многогранники.
Основная цель – познакомить учащихся с основными видами многогранников (призма, пирамида, усеченная пирамида), с формулой Эйлера для выпуклых многогранников, с правильными многогранниками и элементами их симметрии.
Векторы в пространстве (7ч).
Понятие вектора в пространстве. Сложение и вычитание векторов. Умножение вектора на число. Компланарные векторы.
Основная цель – ввести понятие вектора в пространстве, сформировать представления учащихся о сложении и вычитании векторов, умножении вектора на число, компланарных векторах.
Повторение. Решение задач. Итоговая контрольная работа. (11ч).
Требования к уровню подготовки учащихся
В результате изучения математики на профильном уровне ученик должен знать/понимать:
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
вероятностный характер различных процессов окружающего мира;
роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе.
Тема: Числовые и буквенные выражения. Начала математического анализа.
Учащийся должен уметь:
выполнять арифметические действия, сочетая устные и письменные приёмы, применение вычислительных устройств; находить значение корня натуральной степени, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчётах; выполнять действия с комплексными числами, пользоваться геометрической интерпретацией комплексных чисел, в простейших случаях находить комплексные корни уравнений с действительными коэффициентами.
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени и тригонометрические функции;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования.
Использовать приобретённые знания и умения в практической деятельности и повседневной жизни для решения прикладных задач, в том числе социально-экономических и физических – на наибольшее и наименьшее значения, на нахождение скорости и ускорения.
Тема: Уравнения и неравенства
Учащийся должен уметь:
решать тригонометрические уравнения и их системы;
составлять уравнения и неравенства по условию задачи;
использовать для приближенного решения уравнений и неравенств графический метод;
изображать на координатной плоскости множества решений простейших уравнений и их систем.
Использовать приобретённые знания и умения в практической деятельности и повседневной жизни для построения и исследования простейших математических моделей.
Тема: Функции и графики
Учащийся должен уметь:
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций;
описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшее и наименьшее значения;
решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков.
Использовать приобретённые знания и умения в практической деятельности и повседневной жизни для описания с помощью функций различных зависимостей, представления их графически, для интерпретации графиков.
Тема: Элементы комбинаторики
Учащийся должен уметь:
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
анализа реальных числовых данных, представленных в виде диаграмм, графиков.
Критерии и нормы оценки знаний, умений и навыков обучающихся по алгебре и началам анализа 1. Оценка письменных контрольных работ.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2. Оценка устных ответов.
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала;
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Требования к математической подготовке учащихся по геометрии
Уметь решать простые задачи по всем изученным темам, выполняя стереометрический чертеж.
Уметь описывать взаимное расположение прямых и плоскостей в пространстве.
Уметь анализировать в простейших случаях взаимное расположение объектов в пространстве.
Уметь изображать основные многоугольники; выполнять чертежи по условию задач.
Уметь строить простейшие сечения куба, призмы, пирамиды.
Уметь решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей).
Уметь использовать при решении стереометрических задач планиметрические факты и методы.
Уметь распознавать на чертежах и моделях пространственные формы.
Уметь описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении.
Проводить доказательные рассуждения в ходе решения задач.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: исследования (моделирования) практических ситуаций на основе изученных формул и свойств фигур; вычисления площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Критерии и нормы оценки знаний, умений и навыков обучающихся по геометрии 1. Оценка письменных контрольных работ обучающихся по геометрии.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обоснованиях решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны;
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах.
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2. Оценка устных ответов обучающихся по геометрии.
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала;
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Ресурсное обеспечение программы (литература):
Алгебра и начала математического анализа. 10 класс. Часть 1.: учебник / А.Г.Мордкович, П.В. Семенов –2е изд. - М.: МНЕМОЗИНА, 2010.
Алгебра и начала математического анализа. 10 класс. Часть 2.: задачник / А.Г.Мордкович, П.В. Семенов –2-е изд. - М.: МНЕМОЗИНА, 2010.
Алгебра и начала математического анализа. Контрольные работы.10 класс профильный уровень / В.И.Глизбург под редакцией А.Г.Мордковича.– М.: Мнемозина, 2009.
Алгебра и начала математического анализа. Самостоятельные работы.10 класс / Л.А.Александрова под редакцией А.Г.Мордковича.– М.: Мнемозина, 2008.
Атанасян Л.С. Геометрия. Учебник для 10-11 классов общеобразовательных учреждений. Обязательный и профильный уровни. - М., «Просвещение», 2010.
Бурмистрова Т.А. Геометрия. 10 - 11 классы. Программы общеобразовательных учреждений. - М., «Просвещение», 2009.
Дорофеев Г. В. и др. Оценка качества подготовки выпускников средней (полной) школы по математике. - М., «Дрофа», 2002.
Федеральный компонент государственного стандарта среднего (полного) общего образования по математике //»Вестник образования» - 2004 - № 14 - с.107-119.
А.П. Ершова, В.В. Голобородько Самостоятельные и контрольные работы по алгебре и началам анализа для 10 – 11 кл. (разноуровневые дидактические материалы) / М.: Илекса, 2003.
Р.Д.Лукин, Т.К. Лукина Устные упражнения по алгебре и началам анализа: Книга для учителя / М.: Просвещение, 1989.
Б.Г. Зив Дидактические материалы по геометрии для 11 кл. / М.: Просвещение, 2004.
С.М. Саакян, В.Ф. Бутусов Изучение геометрии в 10 – 11 кл. : методические рекомендации к учебнику. Книга для учителя / М.: Просвещение, 2004.
А.П. Ершова, В.В. Голобородько Самостоятельные и контрольные работы по геометрии для 10 кл. (разноуровневые дидактические материалы) / М.: Илекса, 2003.
Б.Г. Зив и др. Задачи по геометрии для 7 – 11 классов / М.: Просвещение, 1991.
Е.М. Рабинович Задачи и упражнения на готовых чертежах. Геометрия / М.: Илекса, 2001.
Календарно-тематическое планирование
Пункт
§
|
Содержание материала
|
Кол-во
часов
|
Алгебра
|
Повторение материала 7 – 9 классов
|
3 ч
|
|
Действительные числа
|
12 ч
|
§ 1
|
Натуральные и целые числа. Делимость чисел.
|
3 ч
|
§ 2
|
Рациональные числа.
|
1 ч
|
§ 3
|
Иррациональные числа.
|
1 ч
|
§ 4
|
Множество действительных чисел.
|
2 ч
|
§ 5
|
Модуль действительного числа.
|
2 ч
|
|
Контрольная работа №1
|
1 ч
|
§ 6
|
Метод математической индукции.
|
2 ч
|
Геометрия
|
Аксиомы геометрии и их следствие.
|
6 ч
|
1-2
|
Аксиомы стереометрии.
|
1 ч
|
3
|
Некоторые следствия из аксиом.
|
1 ч
|
|
Решение задач. Самостоятельная работа.
|
4 ч
|
|
Параллельность прямых, прямых и плоскостей
|
5 ч
|
4-5
|
Параллельность прямых в пространстве.
|
1 ч
|
6
|
Параллельность прямой и плоскости.
|
1 ч
|
|
Решение задач. Самостоятельная работа.
|
3 ч
|
|
Взаимное расположение прямых в пространстве.
|
5 ч
|
7
|
Скрещивающиеся прямые.
|
1 ч
|
8-9
|
Угол между прямыми.
|
1 ч
|
|
Решение задач.
|
2 ч
|
|
Контрольная работа №2
|
1 ч
|
Алгебра
|
Числовые функции.
|
10 ч
|
§ 7
|
Определение числовой функции и способы ее задания.
|
3 ч
|
§ 8
|
Свойства функций.
|
3 ч
|
§ 9
|
Периодические функции.
|
1 ч
|
§ 10
|
Обратные функции.
|
2 ч
|
|
Контрольная работа № 3
|
1 ч
|
Геометрия
|
Параллельность плоскостей. Тетраэдр и параллелепипед.
|
10 ч
|
10-11
|
Параллельные плоскости. Свойства параллельных плоскостей.
|
2 ч
|
12-13
|
Тетраэдр. Параллелепипед.
|
2 ч
|
14
|
Задачи на построение сечений.
|
3 ч
|
|
Решение задач.
|
2 ч
|
|
Контрольная работа №4
|
1 ч
|
Алгебра
|
Тригонометрические функции.
|
24 ч
|
§ 11
|
Числовая окружность.
|
2 ч
|
§ 12
|
Числовая окружность на координатной плоскости.
|
2 ч
|
§ 13
|
Синус и косинус. Тангенс и котангенс.
|
3 ч
|
§ 14
|
Тригонометрические функции числового аргумента.
|
2 ч
|
§ 15
|
Тригонометрические функции углового аргумента.
|
1 ч
|
§ 16
|
Функции  , их свойства и графики. , их свойства и графики.
|
3 ч
|
|
Контрольная работа № 5
|
1 ч
|
Геометрия
|
Перпендикулярность прямых и плоскостей.
|
6 ч
|
15-16
|
Перпендикулярность прямых в пространстве.
|
1 ч
|
17-18
|
Признак перпендикулярности прямой и плоскости.
|
2 ч
|
|
Решение задач. Самостоятельная работа.
|
3 ч
|
|
Перпендикуляр и наклонные.
|
6 ч
|
19-20
|
Теорема о трех перпендикулярах.
|
2 ч
|
21
|
Угол между прямой и плоскостью.
|
1 ч
|
|
Решение задач. Самостоятельная работа.
|
3 ч
|
|
Перпендикулярность плоскостей
|
8 ч
|
22-23
|
Двугранный угол. Признак перпендикулярности двух плоскостей.
|
2 ч
|
24
|
Прямоугольный параллелепипед.
|
2 ч
|
|
Решение задач.
|
3 ч
|
|
Контрольная работа №6
|
1 ч
|
Алгебра
§ 17
|
Построение графика функции 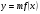 . .
|
2 ч
|
§ 18
|
Построение графика функции 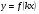 . .
|
2 ч
|
§ 19
|
График гармонического колебания.
|
1 ч
|
§ 20
|
Функции 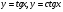 , их свойства и графики. , их свойства и графики.
|
2 ч
|
§ 21
|
Обратные тригонометрические функции.
|
3 ч
|
|
Тригонометрические уравнения.
|
10 ч
|
§ 22
|
Простейшие тригонометрические уравнения и неравенства.
|
4 ч
|
§ 23
|
Методы решения тригонометрических уравнений.
|
4 ч
|
|
Контрольная работа № 7
|
2 ч
|
Алгебра
|
Преобразование тригонометрических выражений
|
21 ч
|
§ 24
|
Синус и косинус суммы и разности аргументов.
|
3 ч
|
§ 25
|
Тангенс суммы и разности аргументов.
|
2 ч
|
§ 26
|
Формулы приведения.
|
2 ч
|
§ 27
|
Формулы двойного аргумента. Формулы понижения степени.
|
3 ч
|
§ 28
|
Преобразование суммы тригонометрических функций в произведение.
|
3 ч
|
§ 29
|
Преобразование произведения тригонометрических функций в сумму.
|
2 ч
|
§ 30
|
Преобразование выражения 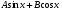 к виду к виду 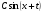 . .
|
1 ч
|
§ 31
|
Методы решения тригонометрических уравнений.
|
3 ч
|
|
Контрольная работа № 8
|
2 ч
|
Геометрия
|
Многогранники.
|
14 ч
|
27-30
|
Понятие многогранника. Призма. Самостоятельная работа.
|
5 ч
|
32-34
|
Пирамида. Правильная пирамида. Усеченная пирамида. Самостоятельная работа.
|
5 ч
|
35-37
|
Симметрия в пространстве. Понятие правильного многогранника.
|
1 ч
|
|
Решение задач
|
2 ч
|
|
Контрольная работа №9
|
1 ч
|
Алгебра
|
Комплексные числа.
|
9 ч
|
§ 32
|
Комплексные числа и арифметические операции над ними.
|
2 ч
|
§ 33
|
Комплексные числа и координатная плоскость.
|
1 ч
|
§ 34
|
Тригонометрическая форма записи комплексного числа.
|
2 ч
|
§ 35
|
Комплексные числа и квадратные уравнения.
|
1 ч
|
§ 36
|
Возведение комплексного числа в степень. Извлечение кубического корня из комплексного числа.
|
2 ч
|
|
Контрольная работа № 10
|
1 ч
|
Алгебра
|
Производная.
|
29 ч
|
§ 37
|
Числовые последовательности.
|
2 ч
|
§ 38
|
Предел числовой последовательности.
|
2 ч
|
§ 39
|
Предел функции.
|
2 ч
|
§ 40
|
Определение производной.
|
2 ч
|
§ 41
|
Вычисление производных
|
3 ч
|
§ 42
|
Дифференцирование сложной функции. Дифференцирование обратной функции.
|
2 ч
|
§ 43
|
Уравнение касательной к графику функции.
|
3 ч
|
|
Контрольная работа № 11
|
2 ч
|
§ 44
|
Применение производной для исследования функций.
|
3 ч
|
§ 45
|
Построение графиков функций.
|
2 ч
|
§ 46
|
Применение производной для отыскания наибольших и наименьших
значений величин.
|
4 ч
|
|
Контрольная работа № 12
|
2 ч
|
Геометрия
|
Векторы в пространстве.
|
7 ч
|
38-39
|
Понятие вектора. Равенство векторов.
|
2 ч
|
40-42
|
Сложение и вычитание векторов. Сумма нескольких векторов. Умножение вектора на число.
|
2 ч
|
43-45
|
Компланарные векторы. Разложение вектора по трем некомпланарным векторам. Самостоятельная работа.
|
3 ч
|
Алгебра
|
Комбинаторика и вероятность.
|
8 ч
|
§ 47
|
Правило умножения. Комбинаторные задачи. Перестановки и факториалы.
|
3 ч
|
§ 48
|
Выбор нескольких элементов. Биноминальные коэффициенты.
|
2 ч
|
§ 49
|
Случайные события и их вероятности.
|
3 ч
|
|
Повторение
|
16 ч
|
|
Итоговая контрольная работа по алгебре и началам анализа.
|
2 ч
|
|
Итого
|
204ч
| |
|
|
 Скачать 308.46 Kb.
Скачать 308.46 Kb. , их свойства и графики.
, их свойства и графики.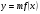 .
.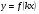 .
.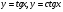 , их свойства и графики.
, их свойства и графики.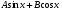 к виду
к виду 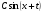 .
.