Методика изучения темы «Уравнения с одной переменной» Анализ содержания программы по математике
 Скачать 97.67 Kb. Скачать 97.67 Kb.
|
| Методика изучения темы «Уравнения с одной переменной» 1. Анализ содержания программы по математике Изучение темы «Уравнения с одной переменной» курса алгебры 7 класса входит в программу экзамена. Поэтому контроль знаний, умений и навыков учащихся очень важен при изучении данного раздела алгебры, от этого зависит успешность сдачи экзамена. Для того чтобы определиться с выбором форм проверки, необходимо выделить содержание контроля. Для начала необходимо сделать анализ программы, затем анализ содержания темы учебника, а затем, в соответствии с ним, выбрать формы и методы контроля. В курсе алгебры в 7 классе содержатся задания теоретического и прикладного характера. Прикладная направленность курса обеспечивается систематическим обращением к примерам, раскрывающим возможности применения математики к изучению действительности и решению практических задач. Целью изучения этого курса является развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов (физика, химия, основы информатики и вычислительной техники и другие), усвоение аппарата функций как основного средства математического моделирования, решение прикладных задач, осуществление функциональной подготовки школьников. В связи с этим программа курса математики предполагает следующее содержание по изучению линейных уравнений с одной переменной в 7 классе основной школы: – Уравнение с одной переменной. Корни уравнения. Линейное уравнение. – Решение текстовых задач методом составления уравнений. В соответствии с программой требования к математической подготовке учащихся: – понимать, что уравнения – это математический аппарат решения разнообразных задач из математики, смежных областей знаний, практики; – правильно употреблять термины «уравнение», «корень уравнения», понимать их в тексте, в речи учителя, понимать формулировку задачи «решить уравнение»; – решать линейные уравнения; – решать текстовые задачи с использованием уравнений. При организации учебного процесса следует опираться на тематическое планирование учебного материала, в котором разработано поурочное планирование, ориентированное на учебник алгебры 7 класса. Анализ содержания тем, связанных с изучением уравнений позволяет продумать эффективный систематический контроль. 2. Уравнения с одной переменной
3. Примеры уранений и алгоритмы решения уравнений. Пример 1. Решите уравнение: 4х = 32. Решение. Корнем уравнения является х = 8, так как 4·8 = 32 верное равенство. Ответ: х = 8. Пример 2. Решите уравнение 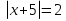 . .Решение. Уравнение имеет два корня: х + 5 = 2 или 2) х + 5 = – 2 х = – 3 х = 3 Ответ: – 3; 3. Пример 3. Решите уравнение – 2(х + 6) = x + 6 . Решение. Шаг 1. Раскроем скобки: – 2х – 12 = х + 6. Шаг 2. Все члены уравнения, содержащие неизвестное, переносим в одну сторону уравнения, а все остальные – в другую. При переносе через знак равенства, знак, стоящий перед соответствующим членом уравнения, меняется на противоположный: – 2х – х = 6 + 12. Шаг 3. Приведем подобные члены: – 3х = 18. Шаг 4. Находим х: х = – 6. Ответ: – 6. Пример 4. Решите уравнение 2t – 3(2 – 6t) = 4(t + 6). Решение. Шаг 1. Раскроем скобки: 2t – 6 +18t = 4t +24. Шаг 2. Все члены уравнения, содержащие неизвестное, переносим в одну сторону уравнения, а все остальные – в другую: 2t – 4t +18t = 24 + 6. Шаг 3. Приведем подобные члены: 16t = 30. Шаг 4. Находим неизвестное и записываем ответ: 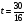 , ,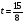 . .Ответ: 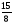 . .Пример 5. Решите уравнение (7х – 2)(3 – 5х) =0. Условие равенства нулю произведения: произведение двух выражений равно нулю тогда и только тогда, когда одно из этих выражений обращается в нуль, а другое при этом не теряет смысла. В данном примере оба сомножителя определены для любого действительного числа х, т.е. при любом значении числа х ни один из сомножителей не теряет смысла, следовательно, равенство нулю произведения равносильно совокупности условий: либо один, либо другой сомножитель равен нулю. При увеличении числа сомножителей, соответственно увеличивается количество условий. Решение. 7х – 2 = 0 или 3 – 5х =0; 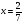 или или 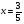 . .Ответ: 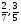 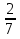 . .Пример 6. Решите уравнение 0,5 (1 – 8х) – 1,5(6х – 3) = 3х –13. Решение. Шаг 1. Раскроем скобки: 0,5 – 4х – 9х + 4,5 = 3х – 13. Шаг 2. Все члены уравнения, содержащие неизвестное, переносим в одну сторону уравнения, а все остальные – в другую: – 8х – 9х – 3х = – 13 – 4,5 – 0,5. Шаг 3. Приведем подобные члены: – 18х = – 18. Шаг 4. Находим неизвестное и записываем ответ: х = 1. Ответ: 1. Пример 7. Решите уравнение 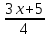 – – – – 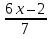 = 1. = 1.Решение. Умножим обе части уравнения на наименьшее общее кратное знаменателей дробей, т. е. на число 28: ( 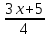 – – 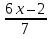 ) · 28= 1·28; ) · 28= 1·28;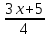 · 28 – · 28 – 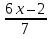 · 28 = 28; · 28 = 28;7(3х + 5) – 4(6х –2) = 28; 21х + 35 – 24х + 8 = 28; – 3х = – 15; х = 5. Ответ: 5. 4. Решение задач с помощью уравнений При решении задач с помощью уравнений необходимо следовать определенному алгоритму: 1) Обозначить некоторое неизвестное число буквой; 2) используя условие задачи, составить уравнение; 3) решить уравнение; 4) полученный результат привести в соответствие с условием задачи. Пример 8. Периметр прямоугольника 28 см, причем одна из его сторон на 4 см больше, чем другая. Найти стороны и площадь прямоугольника. Решение. 1) Пусть ширина прямоугольника х см, тогда его длина (х + 4) см. 2) Из условия задачи известно, что периметр прямоугольника равен 28 см, составим уравнение: 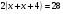 . . 3) Решим уравнение: 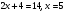 . .Значит, ширина прямоугольника равна 5 см. 4) Зная ширину прямоугольника и зависимость длины от ширины, найдем сначала его вторую сторону, а затем и площадь. х + 4 = 5 + 4 = 9 (см), 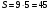 (см2). (см2).Ответ: 9 см, 45 см2. Пример 9. Один арбуз на 5 кг легче, чем второй и в 3 раза легче, чем третий. Первый и третий вместе в 2 раза тяжелее, чем второй. Найти массу второго арбуза. Решение. Пусть первый арбуз весит х кг, тогда второй – (х + 5) кг, а третий – 3х кг. 2) По условию первый и третий в 2 раза тяжелее второго, составим и решим уравнение: х + 3х = 2(х + 5), 4х = 2х + 10, 2х = 10; х = 5. Значит, 5 кг весит первый арбуз, 5 + 5 = 10 (кг) – второй, а 3×5 =15(кг) – третий арбуз. Ответ: 5кг; 10 кг; 15 кг. Пример 10. Катер преодолевает расстояние между пунктами А и В, двигаясь по течению, за 2 часа. На обратный путь он затрачивает 3 часа, двигаясь с той же скоростью. Какое расстояние преодолевает катер на маршруте, и какова его собственная скорость, если скорость течения 5 км/ч ? Решение. 1) Пусть х км/ч – собственная скорость катера. Тогда (х + 5) км/ч – скорость катера по течению, а (х – 5) км/ч – скорость катера против течения. 2) Учитывая время движения катера, составим уравнение: 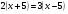 . .3) Решим уравнение: 2х + 10 = 3х – 15; х = 25. Значит, 25 км/ч – собственная скорость катера. 4) (25 + 5)·2 = 60 (км) – расстояние, которое преодолевает катер на маршруте. Ответ: 60 км, 25 км/ч. Пример 11. Из пунктов А и В навстречу друг другу выехали одновременно два велосипедиста, мужчина и женщина. Скорость мужчины была на 3 км/ч больше. Через два часа они встретились, а еще через 3 часа женщина прибыла в пункт А. Какое расстояние (S) между этими пунктами? Решение.  1) Пусть х км/ч – скорость женщины, Тогда (х +3) км/ч – скорость мужчины. Скорость сближения (их совместная скорость) – (2х + 3) км/ч, 2) Весь путь мужчина и женщина преодолели за 2 часа, а женщина на весь путь затратила 5 часов, учитывая это, составим уравнение: 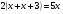 . .3) Решим уравнение: 4х + 6 = 5х; х = 6. Значит, 6 км/ч – скорость женщины. 4) 6 + 3 = 9 (км/ч) – скорость мужчины. Тогда расстояние между пунктами А и В: 6 · 5 = 30 (км). Ответ: 30 км. Пример 12. Отцу 42 года, а сыну 15 лет. Через сколько лет сын будет в два раза моложе отца? Решение. 1) Пусть х – количество лет, через которое сын будет в два раза моложе отца. 2) Тогда можно составить уравнение: 42 + х = 2(15 + х). 3) Решим уравнение: 42 + х = 30 + 2х; х =12. Ответ: через 12 лет. В некоторых случаях при решении задачи целесообразно составить таблицу. Пример 13. В корзине яблок в 4 раза меньше, чем в ящике. После того как из ящика переложили в корзину 1,5 кг яблок, в корзине стало в 3 раза меньше яблок, чем в ящике. Сколько килограммов яблок было в корзине и ящике сначала? Решим эту задачу, следуя алгоритму. Внесем данные в таблицу:
Составим и решим уравнение: 4х – 1,5 = 3 (х + 1,5), 4х – 1,5 = 3х + 4,5, 4х – 3х = 4,5 + 1,5, х = 6. 6 × 4 = 24 (кг). Ответ: 24 кг и 6 кг. Пример 14. С одной станции выехал поезд со скоростью 48 км/ч, а через 2 часа с другой станции навстречу ему вышел поезд со скоростью 60 км/ч. Расстояние между станциями 528 км. Сколько времени в дороге был каждый поезд до встречи. Составим к этой задаче таблицу:
Решение. Какое расстояние прошел первый поезд за 2 часа? 48×2 = 96 (км). Какое расстояние стало между поездами с момента выхода второго поезда? 528 – 96 = 432 (км). До встречи они были в дороге одинаковое количество временами? Обозначив это время за х, составим уравнение: 48х + 60х = 432, 108х = 432, х = 4. 4 часа был в дороге второй поезд, 4 + 2 = 6 (ч) был в дороге первый поезд с момента своего выхода. Ответ: 4 часа и 6 часов. |
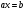 ?
?