Программа по математике для основного общего образования (Базовый уровень) Пояснительная записка

Скачать 0.54 Mb. Название Программа по математике для основного общего образования (Базовый уровень) Пояснительная записка страница 6/7 Дата 13.02.2016 Размер 0.54 Mb. Тип Программа

Перечень выполнения практической части по учебной дисциплине:

Глава XIV П о в т о р е н и е
	Выражения, тождества, уравнения
	Функции
	Степень с натуральным показателем
	Многочлены
	Формулы сокращённого умножения
	Системы линейных уравнений
	Итоговая контрольная работа
	Анализ контрольной работы
	Обобщение и систематизация изученного материала
	Обобщение и систематизация изученного материала

№ урока	Название темы урока	Тип урока	Дата проведения
			По плану	По факту
11	Контрольная работа №1 «Преобразование выражений»	Контроль усвоения знаний
20	Контрольная работа №2 по теме «Основные свойства простейших геометрических фигур»	Контроль усвоения знаний
33	Контрольная работа №3 «Уравнения с одной переменной»	Контроль усвоения знаний
42	Контрольная работа №4 по теме «Смежные и вертикальные углы»	Контроль усвоения знаний
56	Контрольная работа №5 «Функции»	Контроль усвоения знаний
69	Контрольная работа №6 по теме «Признаки равенства треугольников»	Контроль усвоения знаний
84	Контрольная работа №7 «Степень и её свойства»	Контроль усвоения знаний
95	Контрольная работа №8 по теме «Сумма углов треугольника»	Контроль усвоения знаний
106	Контрольная работа №9 «Многочлен»	Контроль усвоения знаний
114	Контрольная работа №10 по теме «Геометрические построения»	Контроль усвоения знаний
123	Контрольная работа № 11 «Произведение многочленов»	Контроль усвоения знаний
135	Контрольная работа №12 «Формулы сокращённого умножения»	Контроль усвоения знаний
143	Контрольная работа №13 «Применение формул сокращённого умножения»	Контроль усвоения знаний
160	Контрольная работа № 14 «Системы линейных уравнений»	Контроль усвоения знаний
167	Итоговая контрольная работа	Контроль усвоения знаний

КОНТРОЛЬНАЯ РАБОТА №1

ВАРИАНТ 1

1. 
   Найдите значение числового выражения:
   

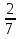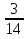( + ) : (7,5 – 13,5)

2. Упростите выражение:

а) 5а – 3b – 8а + 12 b

б) 16с + (3с – 2) – (5с + 7)

в) 7 – 3(6y – 4)

3. Сравните значения выражений 0,5х – 4 и 0,6х – 3 при х = 5

4. Упростите выражение 6,3х – 4 – 3(7,2х + 0,3) и найдите его значение при х =

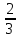
5. В прямоугольном листе жести со сторонами х см и y см вырезали квадратное отверстие со стороной 5 см. Найдите площадь оставшейся части. Решите задачу при х = 13, y = 22.

6. Раскрыть скобки –(15-5а-(12а-(7а-2)) и привести подобные слагаемые

КОНТРОЛЬНАЯ РАБОТА №1

ВАРИАНТ 2

2. 
   Найдите значение числового выражения:
   

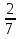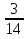( - )( - 7,5 + 13,5)

2. Упростите выражение:

а) 3а + 7b – 6а - 4 b

б) 8с + (5 – с) – (7 + 11с)

в) 4 – 5(3y + 8)

3. Сравните значения выражений 3 – 0,2а и 5 – 0,3а при а = 16

4. Упростите выражение 3,2 а – 7 – 7(2,1а - 0,3) и найдите его значение при а =

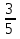
5. В кинотеатре n рядов по m мест в каждом. На дневной сеанс были проданы билеты на первые 7 рядов. Сколько незаполненных мест было во время сеанса? Решите задачу при n = 21, m = 35.

6 Раскройте скобки и приведите подобные слагаемые –(5n-2(8n-4))-11n


Контрольная работа №2

Вариант 1

1. Луч с проходит между сторонами угла (ab), равного 40^. Найдите угол (ac), если угол (bc) = 23^.

2. На отрезке AB длиной 20 см отсечена точка С. Найдите длину отрезка АС, если он больше отрезка ВС на 4 см.

3. Точки А, В и С лежат на одной прямой. Известно, что АВ = 3 см, ВС = 5 см, АС = 2 см. Принадлежит ли точка С отрезку АВ? Объясните ответ.

4. Из точки А проведены лучи АМ, AN, AK. Чему равен угол NAK, если MAN = 76^, MAK =46^.

Вариант 2

1. Луч с проходит между сторонами угла (ab), равного 97^. Найдите угол (bc), если угол (ac) = 53^.

2. На отрезке AB длиной 20 см отсечена точка С. Найдите длину отрезка АС, если он больше отрезка ВС в 4 раза.

3. Проходит ли луч с между сторонами угла (ab), если угол (ab) = 90^, (ac) = 30^, (cb) = 120^? Объясните ответ.

4. Из точки М проведены лучи МО, МN, МK. Чему равен угол NМK, если ОMN = 78^, ОMK =44^.

КОНТРОЛЬНАЯ РАБОТА №3

ВАРИАНТ 1

1. 
   Решите уравнение:
   

а) 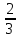х = -6 в) 8х-7,5=6х+1,5

б) 5х - 8,5=0 г) 4х –(9х – 6)=46

2. Турист проехал в 7 раз большее расстояние, чем прошел пешком. Весь путь туриста составил 24 км. Какое расстояние турист проехал?

3.Найти размах, моду и медиану числового ряда:
1, 1, 2, 2, 2, 3, 5, 5, 6, 6, 6, 9

4. В одном мешке соли в 3 раза больше, чем в другом. Когда из первого мешка взяли 11 кг , а во второй добавили 21 , то в обоих мешках стало соли поровну. Сколько тонн соли первоначально в каждом мешке?

5. Решите уравнение 8х – (6 – х)=3(3х-2)


КОНТРОЛЬНАЯ РАБОТА №3

ВАРИАНТ 2

1. 
   Решите уравнение:
   

а) - 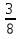х = 24 в) 9х – 8,5= 7х+0,5

б) 7х+10,5=0 г)6х – (9х+7)=11

2. На одной полке на 15 книг большее, чем другой. Всего на двух полках 53 книги. Сколько книг на каждой полке?

3. Найти размах, моду и медиану числового ряда:

-4, -2, -2, -1, 0, 2, 2, 2, 2, 5, 7, 8

4. На одном складе винограда было вдвое меньше, чем на другом. Когда со второго склада отправили в магазины 16 тонн винограда, а на первый склад привезли 25 тонн винограда, то на обоих складах винограда стало поровну. Сколько винограда было на каждом складе первоначально?

5. Решить уравнение 9х – (3х – 4)=2(3х+1)

Контрольная работа №4

Вариант 1

Вариант 1.

1. 
   Один из углов, получившихся при пересечении двух прямых, равен 85°. Вычислите остальные углы.
   
2. 
   Один из смежных углов на 50° больше другого. Найдите меньший угол.
   
3. 
   Один из двух углов, образовавшихся при пересечении двух прямых, на 20° меньше другого. Найдите все углы.
   
4. 
   Из вершины угла проведён луч, перпендикулярный его биссектрисе и образующий со стороной данного угла острый угол, равный 40°. Найдите величину данного угла.
   

Вариант 2.

1. 
   Один из углов, получившихся при пересечении двух прямых, равен 118°. Вычислите остальные углы.
   
2. 
   Один из смежных углов в 4 раза меньше другого. Найдите меньший угол.
   
3. 
   Один из двух углов, образовавшихся при пересечении двух прямых, на 60° больше другого. Найдите все углы.
   

4. Из вершины угла проведён луч, перпендикулярный его биссектрисе и
образующий со стороной данного угла острый угол, равный 50°. Найдите
величину данного угла.

КОНТРОЛЬНАЯ РАБОТА №5

ВАРИАНТ 1

1. 
   Функция задана формулой у = -6х +14. Найдите:
   

а) значение функции y, соответствующее значению аргумента, равному 4;

б) значение аргумента х, при котором значение у= - 8.

2. 
   а) Постройте график функции у= 3х – 4.
   

б) С помощью графика функции найдите значение функции, соответствующее значению аргумента 2.

3. В одной системе координат постройте графики функций у = - 0,5х и у = 2.
4. Проходит ли график функции у = - 5х + 11 через точку М(6; -41)?

5. Каково взаимное расположение графиков функции у = 15х - 51 и у = - 15х + 39 ?

1) параллельные 2) пересекаются 3) перпендикулярные


КОНТРОЛЬНАЯ РАБОТА №5

ВАРИАНТ 2
1. Функция задана формулой у = 2х-9. Найдите:

а) значение функции у, соответствующее значению аргумента, равному -6;

б) значение аргумента х, при котором значение у= -1.

2. 
   а) Постройте график функции у= -2х + 5.
   

б) С помощью графика функции найдите значение функции, соответствующее значению аргумента 5.

3. В одной системе координат постройте графики функций у = 0,5х и у = -5.
4. Проходит ли график функции у = - 7х - 3 через точку М(4; -25)?

5. Каково взаимное расположение графиков функции у = -21х - 15 и у = 21х + 69 ?

1) пересекаются 2) параллельные 3) перпендикулярные
Контрольная работа №6

Вариант 1

1. На основании АС равнобедренного треугольника ABC отложены равные отрезки AD и СЕ. Докажите, что треугольник BАD равен треугольнику ВСЕ.

2. Периметр равнобедренного треугольника равен 16,6 м. Найдите его стороны, если основание больше боковой стороны на 4 см.

3. На биссектрисе угла А взята точка В, а на сторонах угла — точки С и D, такие, что угол ABC = углу ABD. Докажите, что AD = АС.

4. Треугольники ABC и DBC равнобедренные с основанием ВС.

Известно, что АВ = CD. Докажите, что эти треугольники равны.

Вариант 2

1. На основании АС равнобедренного треугольника ABC

отмечены точки М и К так, что угол ABM = углу CBK.

Докажите, ∆АВМ =∆ АСВ

2. 
   Периметр равнобедренного треугольника равен 10,9 м. Найдите его стороны, если боковая сторона на 2 м больше основания.
   
3. 
   Отрезки АВ и CD равны и пересекаются в точке О так, АО = OD. Докажите, что BD = АС.
   
4. 
   В треугольниках ABC и BCD АВ = BD и АС = CD
   Докажите, что луч ВС является биссектрисой угла ABD,
   а луч СВ биссектрисой угла ACD.
   

КОНТРОЛЬНАЯ РАБОТА №7

ВАРИАНТ 1

1. 
   Выполните действия:
   

а) х⁵ х¹¹ в) х¹⁵: х³

б) (х⁴)⁷ г) (3х⁶)³

2. 
   Упростите выражение:
   

а) 4а²с (- 2,5ас⁴) б) ( -2 х¹⁰ у⁶)⁴

3. Постройте график функции у = х²

С помощью графика определите:

а) значение функции при х = -1,5;

б) значение переменной х при у(х) = 3.

4. Найдите значение выражения:

а) 3¹¹ 9³ б) 3х³ – 1 при х = -⅓

27⁵

5. Упростите выражение (- 1 ½ х⁵у¹³)³ 0,08 х⁷у
КОНТРОЛЬНАЯ РАБОТА №7

ВАРИАНТ 2

1. Выполните действия:

а) х⁹ х¹³ в) х¹⁸: х⁶

б) (х⁷)⁴ г) (2х³)⁵

2. Упростите выражение:

а) -7а⁵с³ 1,5ас б) ( -3 х⁴ у¹³)³

3. Постройте график функции у = х²

С помощью графика определите:

а) значение функции при х = 2,5;

б) значение переменной х при у(х) = 5.

4. Найдите значение выражения:

а) 8³ 2⁴ б) 2 - 7х² при х = -½

4⁵

5. Упростите выражение (- 2½ х¹⁵у⁴)² 0,04 ху⁷

Контрольная работа №8

Вариант 1

1. Параллельные прямые а и b пересечены прямой с, с

 1= 122° . 1

Найдите 2.

b

2

a
2. В треугольнике АВС А в 2 раза больше В, а С = 30^. Найдите углы треугольника.
3. В равнобедренном треугольнике MNK с основанием МК
внешний угол при основании в 4 раза больше своего внутреннего.
Вычислите углы треугольника.
Вариант 2

1. Прямая а пересекает параллельные прямые b и с. 1 = 78°. Найдите 2.

b a

2

c 1
2. В треугольнике АВС А на 30^ больше В, а С = 60^. Найдите углы треугольника.

4. 
   В равнобедренном треугольнике ABC с основанием АС внешний угол при вершине В в 2 раза меньше своего внутреннего. Вычислите углы треугольника.
   

КОНТРОЛЬНАЯ РАБОТА №9

ВАРИАНТ 1

1. 
   Упростите выражение -12х + 3ху – 2( х +3ху)
   

2. 
   Решите уравнение:
   

30 + 5(3х – 1) = 35х – 25

3. 
   Вынесите общий множитель за скобки:
   

а) 7ха – 7хb б) 16ху² + 12х²у

4. 
   По плану тракторная бригада должна была вспахать поле за 14 дней. Бригада вспахивала ежедневно на 5 га больше, чем намечалось по плану. И потому закончила пахоту за 12 дней. Сколько гектаров было вспахано?
   
5. 
   Решите уравнение:
   

а) 4х + 5 3х – 2 2х – 5

6 + 4 = 3

б) х² + 8 х = 0
КОНТРОЛЬНАЯ РАБОТА №9

ВАРИАНТ 2

1. Упростите выражение -12х + 3ху – 2( х +3ху)

2. 
   Решите уравнение:
   

10х - 5 = 6(8х + 3) – 5х

2. 
   Вынесите общий множитель за скобки:
   

а) 8ха + 4хb б) 18ху³ + 12х²у

2. 
   Заказ по выпуску машин должен быть выполнен по плану за 20 дней. Но завод выпускал ежедневно по 2 машины сверх плана и поэтому выполнил заказ за 18 дней. Сколько машин должен был выпускать завод ежедневно по плану ?
   
3. 
   Решите уравнение:
   

а) 7х - 4 8 – 2х 3х + 3

9 + 6 = 4

б) 2х² - х = 0

Контрольная работа №10

КОНТРОЛЬНАЯ РАБОТА №11

ВАРИАНТ 1

1. 
   Представьте в виде многочлена:
   

а) ( у – 4)(у – 5) б) (х – 3)(х² + 2х – 6)

в) (3а + 2b)(5а – b)

2. 
   Разложите на множители:
   

а) b(b + 1) – 3(b + 1) б) са – сb + 2а - 2b

3. 
   Упростите выражение:
   

(а² – b²)(2а + b) - аb( а + b)

4. 
   Докажите тождество: ( х - 3)( х + 4) = х( х + 1) – 12.
   

5. 
   Ширина прямоугольника вдвое меньше его длины. Если ширину увеличить на 3 см, а длину – на 2 см, то площадь прямоугольника увеличится на 78 см². Найдите длину и ширину прямоугольника.