Наименование раздела
|
Название темы
|
Содержание учебного материала
|
Требования к уровню подготовки учащихся
|
Алгебраические дроби.
|
1 .Основные понятия.
|
Алгебраическая дробь. Допустимые значения.
|
Знать/понимать:
- основное свойство дроби;
- правила сложения и вычитания дробей с одинаковыми и разными знаменателями;
- правила умножения и деления дробей;
- рациональное выражение, рациональное уравнение;
- степень с целым отрицательным показателем.
Уметь:
-уметь находить допустимые значения переменной;
-уметь сокращать дроби после разложения на множители числителя и знаменателя;
- выполнять действия с алгебраическими дробями;
- упрощать выражения с алгебраическими дробями;
- решать простейшие рациональные уравнения;
- выполнять действия со степенями с отрицательными целыми показателями.
|
2. Основное свойство алгебраической дроби.
|
Основное свойство дроби, сокращение дробей, тождественные преобразования,.
|
3. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями.
|
Сложение и вычитание дробей с одинаковыми знаменателями
|
4. Сложение и вычитание алгебраических дробей с разными знаменателями.
|
Сложение и вычитание дробей с разными знаменателями
|
5. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень.
|
Правило умножения дробей, возведение дробей в степень. Правило деления дробей.
|
6. Преобразование рациональных выражений.
|
Рациональное выражение, сложение, вычитание, умножение, деление рациональных дробей.
|
7. Первые представления о рациональных уравнениях.
|
Рациональное уравнение. Правило решения рациональных уравнений.
|
8. Степень с отрицательным целым показателем
|
Определение степени с отрицательным целым показателем, свойства степени.
|
Контрольные работы № 1,3
|
|
Уметь применять изученный теоретический материал при выполнении письменной работы
|
Функция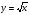 . Свойства квадратного корня. . Свойства квадратного корня.
|
9. Рациональные числа
|
Множество рациональных чисел, бесконечные десятичные периодические дроби, период, чисто периодическая дробь, смешанно периодическая дробью
|
Знать/понимать:
- рациональные числа, бесконечная десятичная периодическая дробь;
- действительные и иррациональные числа;
- о делимости целых чисел, о делении с остатком;
- определение арифметического квадратного корня;
- свойства арифметического квадратного корня;
- определение модуля действительного числа.
Уметь:
- извлекать квадратные корни из неотрицательного числа;
- применять свойства арифметического квадратного корня к преобразованию выражений;
- вычислять значения выражений, содержащих квадратные корни;
- освобождаться от иррациональности в знаменателе;
- исследовать уравнение 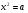 ; ;
- строить график функции 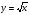 и работать с ним; и работать с ним;
- применять свойства модуля.
|
10. Понятие квадратного корня из неотрицательного числа.
|
Квадратные корни. Арифметический квадратный корень. Уравнение 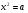 . Нахождение приближенных значений квадратного корня. . Нахождение приближенных значений квадратного корня.
|
11. Иррациональные числа.
|
Иррациональные числа, бесконечная десятичная непериодическая дробь, иррациональные выражения
|
12. Множество действительных чисел
|
Множество действительных чисел, сравнение действительных чисел, действия над действительными числами
|
13. Функция 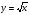 , ее свойства и график. , ее свойства и график.
|
График функции, свойства функции.
|
14. Свойства квадратных корней.
|
Квадратный корень из произведения, квадратный корень из дроби,
вычисление корней
|
15. Преобразование выражений, содержащих операцию извлечения квадратного корня.
|
Преобразование выражений, содержащих операцию извлечения квадратного корня, освобождение от иррациональности в знаменателе
|
16. Модуль действительного числа.
|
Модуль действительного числа, свойства модулей, геометрический смысл модуля действительного
|
Контрольная работа № 4.
|
|
Уметь применять изученный теоретический материал при выполнении письменной работы
|
Квадратичная функция.
Функция 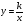
|
17. Функция  , ее свойства и график. , ее свойства и график.
|
Кусочные функции, контрольные точки графика, функция y = kx2, ее свойства и график.
|
Знать/понимать:
- о функциях вида y = kx2 и 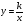 , ,
y = ax2 + bx + c , о их графиках и свойствах;
- как с помощью параллельного построить графики функций y = f(x + l), y = f(x) + m,
y = f(x + l) + m;
- алгоритм построения параболы
y = ax2 + bx + c;
- графические способы решения квадратных уравнений.
Уметь:
- строить графики функций y = kx2, 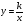 , ,
y = ax2 + bx + c , y = f(x + l), y = f(x) + m,
y = f(x + l) + m;
- описывать свойства функций по ее графику;
- решать графически квадратные уравнения.
|
18. Функция 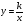 , ее свойства и график. , ее свойства и график.
|
Функция 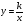 , ее свойства и график при различных значения k. , ее свойства и график при различных значения k.
|
19. Как построить график функции  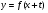 , если известен график функции , если известен график функции 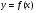 . .
|
Параллельный перенос вправо (влево), вспомогательная система координат, алгоритм построения графика функции
y = f(x + l).
|
20. Как построить график функции 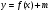 , если известен график функции , если известен график функции 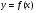 . .
|
Параллельный перенос вверх (вниз), вспомогательная система координат, алгоритм построения графика функции
y = f(x) + m
|
21. Как построить график функции  , если известен график функции , если известен график функции 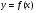 . .
|
Параллельный перенос вправо (влево), параллельный перенос вверх (вниз), вспомогательная система координат, алгоритм построения графика функции
y = f(x + l) + m
|
22. Функция  , ее свойства и график. , ее свойства и график.
|
Функция y = ax2 + bx + c,
квадратичная функция, график квадратичной функции, координаты вершины параболы, алгоритм построения параболы y = ax2 + bx + c
|
23. Графическое решение квадратных уравнений.
|
Квадратное уравнение, несколько способов графического решения уравнения.
|
Контрольные работы № 6,8
|
|
Уметь применять изученный теоретический материал при выполнении письменной работы
|
Квадратные уравнения.
|
24. Основные понятия.
|
Квадратное уравнение, приведенное квадратное уравнение, полное квадратное уравнение, неполное квадратное уравнение, корень квадратного уравнения, решение квадратного уравнения.
|
Знать/понимать:
- квадратные и дробные уравнения;
- способы решения неполных квадратных уравнений;
- формулу корней квадратного уравнения;
- теорему Виета;
- иррациональные уравнения и способы их решения.
Уметь:
- решать квадратные уравнения, а также уравнения сводящиеся к ним;
- решать дробно-рациональные уравнения;
- исследовать квадратное уравнение по дискриминанту и коэффициентам;
- решать текстовые задачи с помощью квадратных и дробно-рациональных уравнений;
- решать иррациональные уравнения.
|
25. Формулы корней квадратных уравнений.
|
Дискриминант квадратного уравнения, формула корней квадратного уравнения.
|
26. Рациональные уравнения.
|
Рациональные уравнения, алгоритм решения рационального уравнения, проверка корней уравнения, посторонние корни
|
27. Рациональные уравнения как математические модели реальных ситуаций.
|
Рациональные уравнения, математическая модель реальной ситуации, решение задач на составление уравнений.
|
28. Еще одна формула корней квадратного уравнения.
|
Квадратное уравнение с четным вторым коэффициентом, формула корней квадратного уравнения с четным вторым коэффициентом.
|
29. Теорема Виета.
|
Теорема Виета, обратная теорема Виета, симметрическое выражение с двумя переменными.
|
30. Иррациональные уравнения.
|
Иррациональные уравнения, метод возведения в квадрат, проверка корней, равносильные уравнения, равносильные преобразования уравнения, неравносильные преобразования уравнения.
|
|
Контрольные работы № 9, 11
|
|
Уметь применять изученный теоретический материал при выполнении письменной работы
|
Неравенства.
|
31. Свойства числовых неравенств.
|
Числовое неравенство, свойства
числовых неравенств, неравенства одинакового смысла, неравенства противоположного смысла, среднее арифметическое, среднее геометрическое, неравенство Коши
|
Знать/понимать:
- определение числового неравенства4
- свойства числовых неравенств;
- стандартный вид числа;
- возрастание, убывание функций.
Уметь:
- находить пересечение и объединение множеств;
- иллюстрировать на координатной прямой числовые неравенства;
- применять свойства числовых неравенств при решении задач;
- решать линейные неравенства;
- решать квадратные неравенства разными способами;
- находить промежутки возрастания и убывания функций;
- записывать числа в стандартном виде.
|
32. Исследование функций на монотонность.
|
Возрастающая функция на промежутке, убывающая функция на промежутке, монотонная функция.
|
33. Решение линейных неравенств.
|
Неравенство с переменной, решение неравенства с переменной, множество решений, система линейных неравенств, пересечение решений неравенств системы.
|
|
34. Решение квадратных неравенств.
|
Квадратное неравенство, знак объединения множеств, алгоритм решения квадратного неравенства, метод интервалов.
|
|
35. Приближенные значения действительных чисел.
|
Приближенное значение по недостатку, приближенное значение по избытку, округление чисел, погрешность приближения, абсолютная и относительная погрешности.
|
|
36. Стандартный вид положительного числа.
|
Стандартный вид положительного числа, порядок числа, запись числа в стандартной форме.
|
|
Контрольная работа № 12
|
|
Уметь применять изученный теоретический материал при выполнении письменной работы
|
Четырехугольники.
|
1.Многоугольники.
|
Многоугольники. Выпуклые многоугольники. Сумма углов выпуклого многоугольника.
|
Знать/понимать:
- Определения: многоугольника, параллелограмма, трапеции, прямоугольника, ромба, квадрата;
- формулу суммы углов выпуклого многоугольника;
- свойства этих четырехугольников;
- признаки параллелограмма;
- виды симметрии.
Уметь:
- распознавать на чертеже многоугольники и выпуклые многоугольники; параллелограммы и трапеции;
- применять формулу суммы углов выпуклого многоугольника;
- применять свойства и признаки параллелограммов при решении задач;
- делить отрезок на n равных частей;
- строить симметричные точки и распознавать фигуры, обладающие осевой и центральной симметрией;
- выполнять чертеж по условию задачи.
|
2.Параллелограмм и трапеция.
|
Параллелограмм и его свойства. Признаки параллелограмма. Трапеция, Средняя линия трапеции. Равнобедренная трапеция и ее свойства. Теорема Фалеса. Задачи на построение.
|
3.Прямоугольник, ромб, квадрат.
|
Прямоугольник и его свойства. Ромб, квадрат их свойства и признаки. Осевая и центральная симметрия, как свойства геометрических фигур.
|
Контрольная работа. № 2.
|
|
Уметь применять изученный теоретический материал при выполнении письменной работы
|
Площадь.
|
1.Площадь многоугольника.
|
Понятие о площади. Равновеликие фигуры. Свойства площадей.
|
Знать/понимать:
- представление о способе измерения площади, свойства площадей;
- формулы площадей: прямоугольника, параллелограмма, треугольника, трапеции;
- формулировку теоремы Пифагора и обратной ей.
Уметь:
- находить площади прямоугольника, параллелограмма, треугольника, трапеции;
- применять формулы при решении задач;
- находить стороны треугольника, используя теорему Пифагора;
- определять вид треугольника, используя теорему, обратную теореме Пифагора.
- выполнять чертеж по условию задачи.
|
2.Площадь параллелограмма, треугольника и трапеции.
|
Формулы площадей прямоугольника, параллелограмма, треугольника, трапеции. Теорема об отношении площадей треугольников имеющих по равному углу.
|
3.Теорема Пифагора.
|
Теорема Пифагора и теорема обратная теореме Пифагора.
|
Контрольная работа № 5
|
|
Уметь применять изученный теоретический материал при выполнении письменной работы
|
Подобные треугольники.
|
1.Определение подобных треугольников.
|
Подобие треугольников. Коэффициент подобия. Связь между площадями подобных фигур.
|
Знать/понимать:
- определение подобных треугольников;
- формулировки признаков подобия треугольников;
- формулировку теоремы об отношении площадей подобных треугольников;
- формулировку теоремы о средней линии треугольника;
- свойство медиан треугольника;
-понятие среднего пропорционального,
- свойство высоты прямоугольного треугольника, проведенной из вершины прямого угла;
- определение синуса, косинуса, тангенса острого угла прямоугольного треугольника
- значения синуса, косинуса, тангенса углов 30º, 45º, 60º, 90º.
Уметь:
- находить элементы треугольников, используя определение подобных треугольников;
- находить отношение площадей подобных треугольников;
- применять признаки подобия при решении задач;
- применять метод подобия при решении задач на построение;
- находить значение одной из тригонометрических функций по значению другой;
- решать прямоугольные треугольники.
|
2.Признаки подобия треугольников.
|
Три признака подобия треугольников.
|
3.Применение подобия к доказательству теорем и решению задач.
|
Средняя линия треугольника. Свойство медиан треугольника. Среднее пропорциональное. Пропорциональные отрезки в прямоугольном треугольнике. Измерительные работы на местности. Метод подобии.
|
4.Соотношения между сторонами и углами прямоугольного треугольника.
|
Понятия синуса, косинуса, тангенса острого угла прямоугольного треугольника. Основное тригонометрическое тождество. Значения синуса, косинуса, тангенса углов 30º, 45º, 60º, 90º.
|
Контрольная работа № 7, 10
|
|
Уметь применять изученный теоретический материал при выполнении письменной работы.
|
Окружность.
|
1.Касательная к окружности.
|
Взаимное расположение прямой и окружности. Касательная и секущая к окружности. Точка касания. Свойство касательной и признак.
|
Знать/понимать:
- случаи взаимного расположения прямой и окружности;
- понятие касательной, точек касания, свойство касательной;
- определение вписанного и центрального углов;
- определение серединного перпендикуляра;
- формулировку теоремы об отрезках пересекающихся хорд;
- четыре замечательные точки треугольника;
- определение вписанной и описанной окружностей.
Уметь:
- определять и изображать взаимное расположение прямой и окружности;
- окружности, вписанные в многоугольник и описанные около него;
- распознавать и изображать центральные и вписанные углы;
- находить величину центрального и вписанного углов;
- применять свойства вписанного и описанного четырехугольника при решении задач;
- выполнять чертеж по условию задачи;
- решать простейшие задачи, опираясь на изученные свойства.
|
2.Центральные и вписанные углы.
|
Центральные и вписанные углы. Градусная мера дуги окружности. Теорема о вписанном угле и следствия из нее. Теорема об отрезках пересекающихся хорд.
|
3.Четыре замечательные точки треугольника.
|
Теорема о свойстве угла биссектрисы. Серединный перпендикуляр. Теорема о серединном перпендикуляре. Теорема о точке пересечения высот треугольника.
|
4.Вписанная и описанная окружности.
|
Вписанная и описанная окружности. Теорема об окружности, вписанной в треугольник. Теорема об окружности, описанной около треугольника. Свойства вписанного и описанного четырехугольника.
|
Контрольная работа № 13
|
|
Уметь применять изученный теоретический материал при выполнении письменной работы
|
Повторение.
|
Алгебра.
Контрольная работа № 14
|
Действия с рациональными дробями. Действия с корнями. Решение квадратных и рациональных уравнений. Решение задач с помощью квадратных и рациональных уравнений. Решение неравенств.
|
|
|
Геометрия.
|
Решение задач по всему курсу.
|
|
 Скачать 175.64 Kb.
Скачать 175.64 Kb.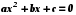 , где
, где  , по формуле корней, что позволяет существенно расширить аппарат уравнений, используемый для решения текстовых задач. Продолжается изучение числовых неравенств, на которых основано решение линейных неравенств с одной переменной. Вводится понятие о числовых промежутках. Изучаются свойства функций
, по формуле корней, что позволяет существенно расширить аппарат уравнений, используемый для решения текстовых задач. Продолжается изучение числовых неравенств, на которых основано решение линейных неравенств с одной переменной. Вводится понятие о числовых промежутках. Изучаются свойства функций 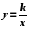 , при
, при 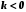 и
и 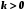 , и
, и 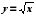 . Выявляется связь функции
. Выявляется связь функции 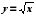 с функцией
с функцией 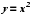 , где
, где  . Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.
. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий. Параллельно закладываются основы для изучения систематических курсов стереометрии, физики, химии и других смежных предметов.
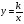
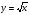 . Свойства квадратного корня.
. Свойства квадратного корня. 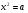 ;
;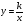
 , ее свойства и график.
, ее свойства и график.
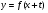 , если известен график функции
, если известен график функции 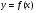 .
.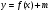 , если известен график функции
, если известен график функции  , если известен график функции
, если известен график функции  , ее свойства и график.
, ее свойства и график.