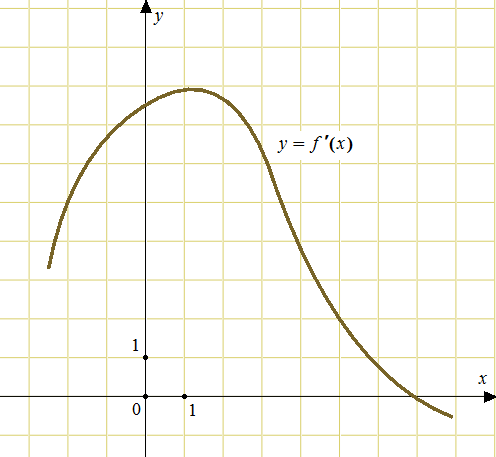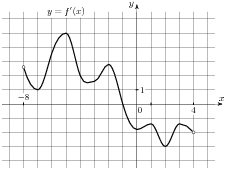
«Геометрический смысл производной. Уравнение касательной»

Скачать 24.12 Kb. Название «Геометрический смысл производной. Уравнение касательной» Дата 05.03.2016 Размер 24.12 Kb. Тип Документы

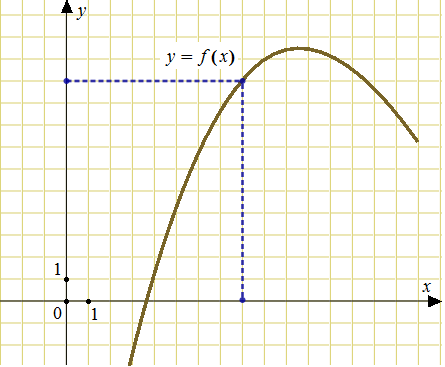
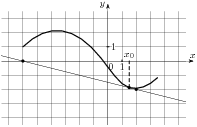
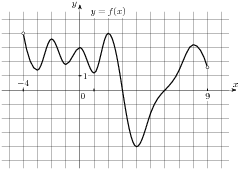
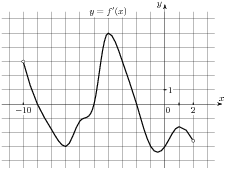
Метапредмет «Задача» Алгебра и начала анализа Рабочий лист ученика 11А класса _____________________________ по теме «Геометрический смысл производной. Уравнение касательной» Актуализация знаний 1.1. Запишите формулу, задающую линейную функцию _____________________________ 1.2. Число ____ называют угловым коэффициентом прямой, а угол α- углом между _____________________________________________________________________________ 1.3. Графики двух линейных функций и : - пересекаются, если ________________________________________________ - совпадают, если ___________________________________________________ - параллельны, если _________________________________________________ 1.4. Геометрический смысл производной состоит в том, что ___________________________________________________________________________________________________________________________________________________________________________________ 1.5. Уравнение касательной имеет вид_____________________________________________ 1.6. Продолжите равенство _____________________ Закрепление и расширение знаний по данной теме при решении прототипов В8 из открытого банка заданий ЕГЭ. Тип задачи Главный вопрос задачи Способ (алгоритм) решения 1. На рисунке изображен график функции . Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите . 2. На рисунке изображён график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке . 3. На рисунке изображен график функции , определенной на интервале (-4; 9). Найдите количество точек, в которых касательная к графику функции параллельна прямой - 1 4. На рисунке изображен график производной функции , определенной на интервале (-10;2). Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней. 5. На рисунке изображен график производной функции . Найдите абсциссу точки, в которой касательная к графику параллельна прямой или совпадает с ней. 6. Функция определена на интервале (-8; 4). На рисунке изображен график производной функции. Укажите абсциссу точки, в которой касательная к графику функции имеет наибольший (наименьший) угловой коэффициент. 7. Дана функция Написать равнение касательной к графику функции , проходящей через точку А(2; -5).