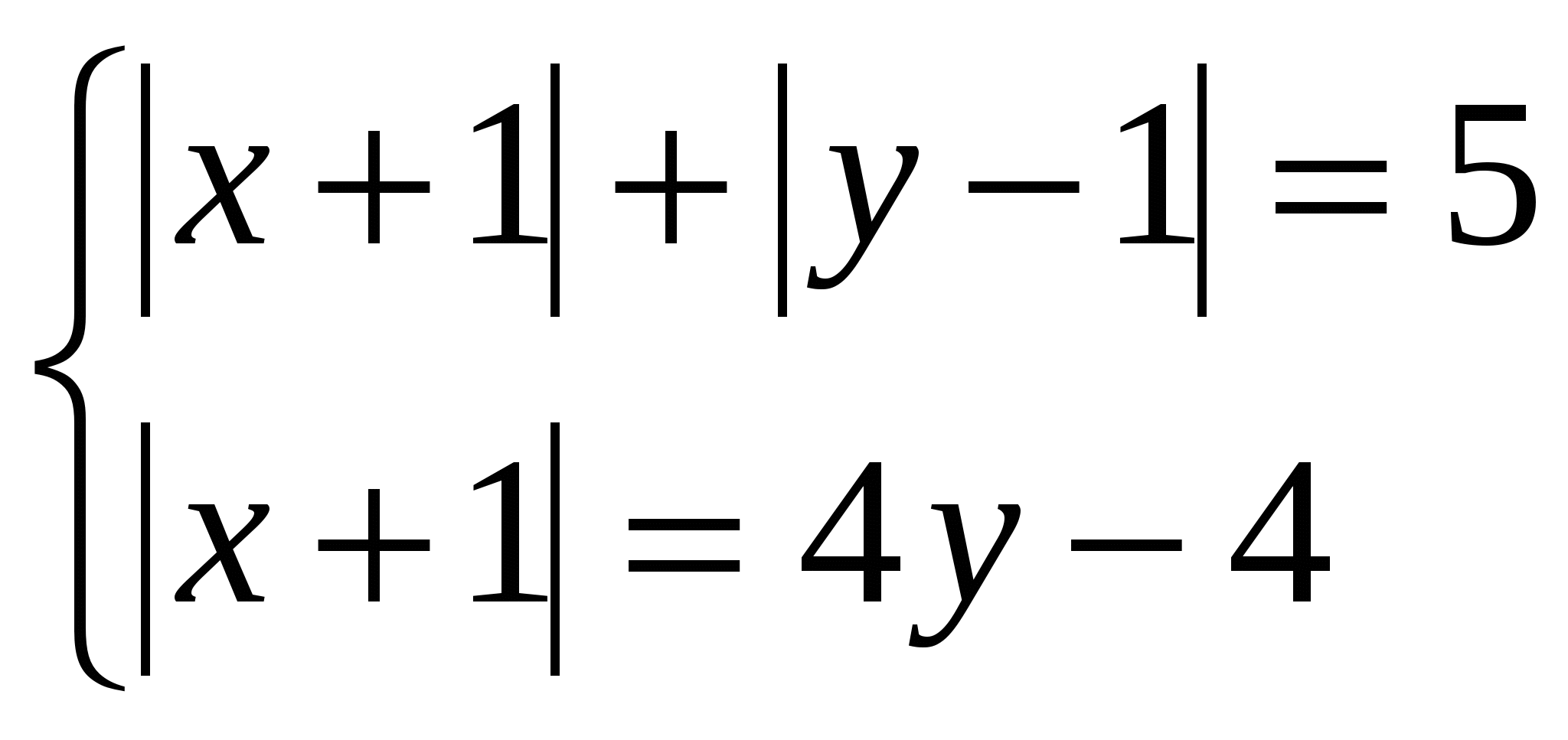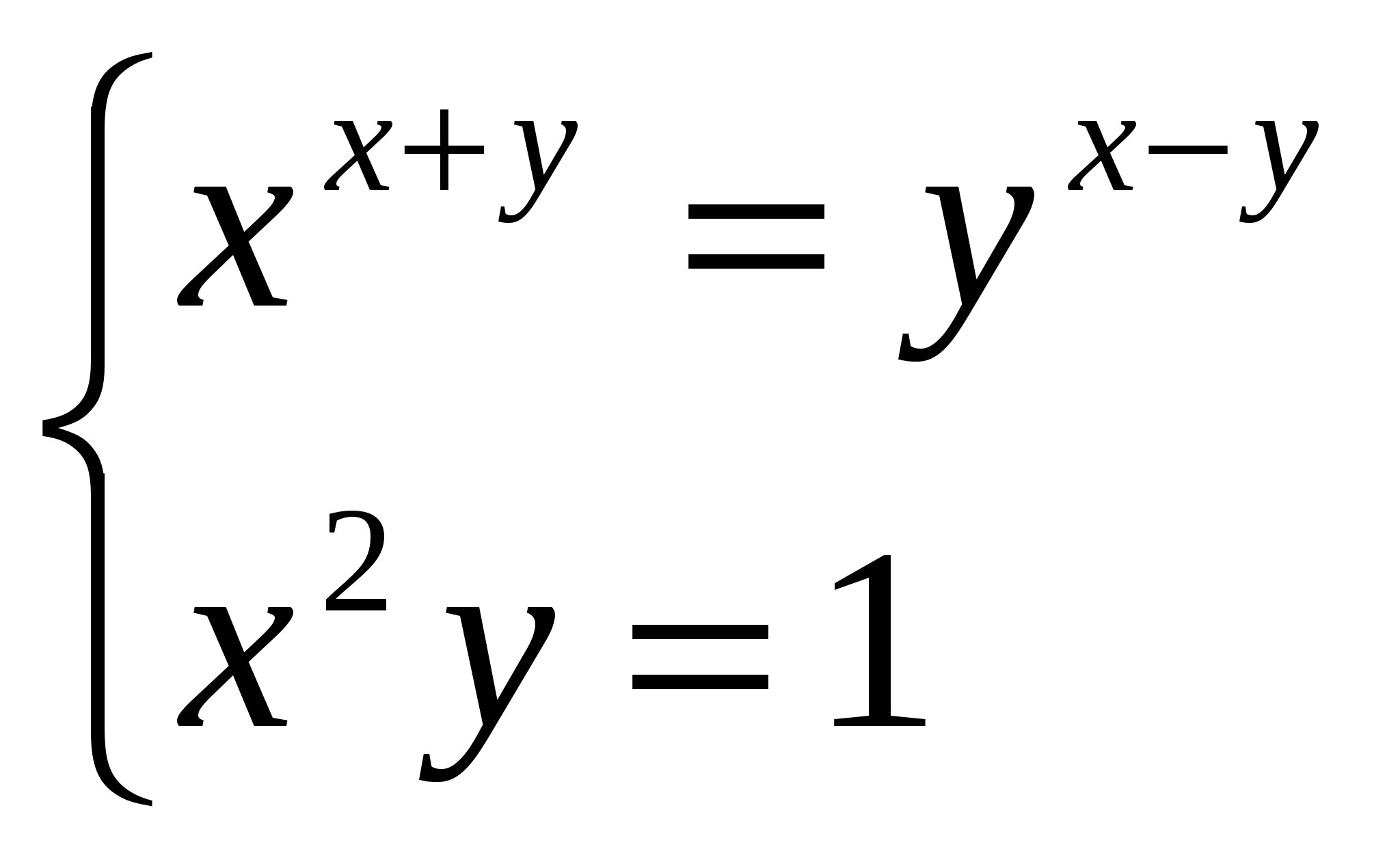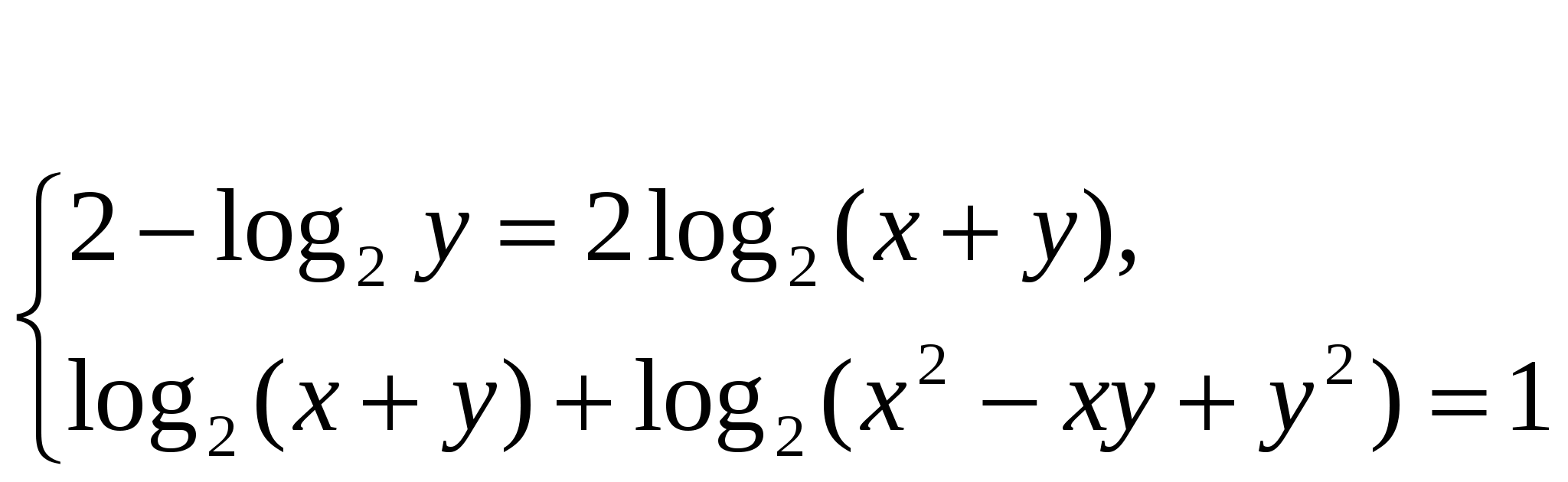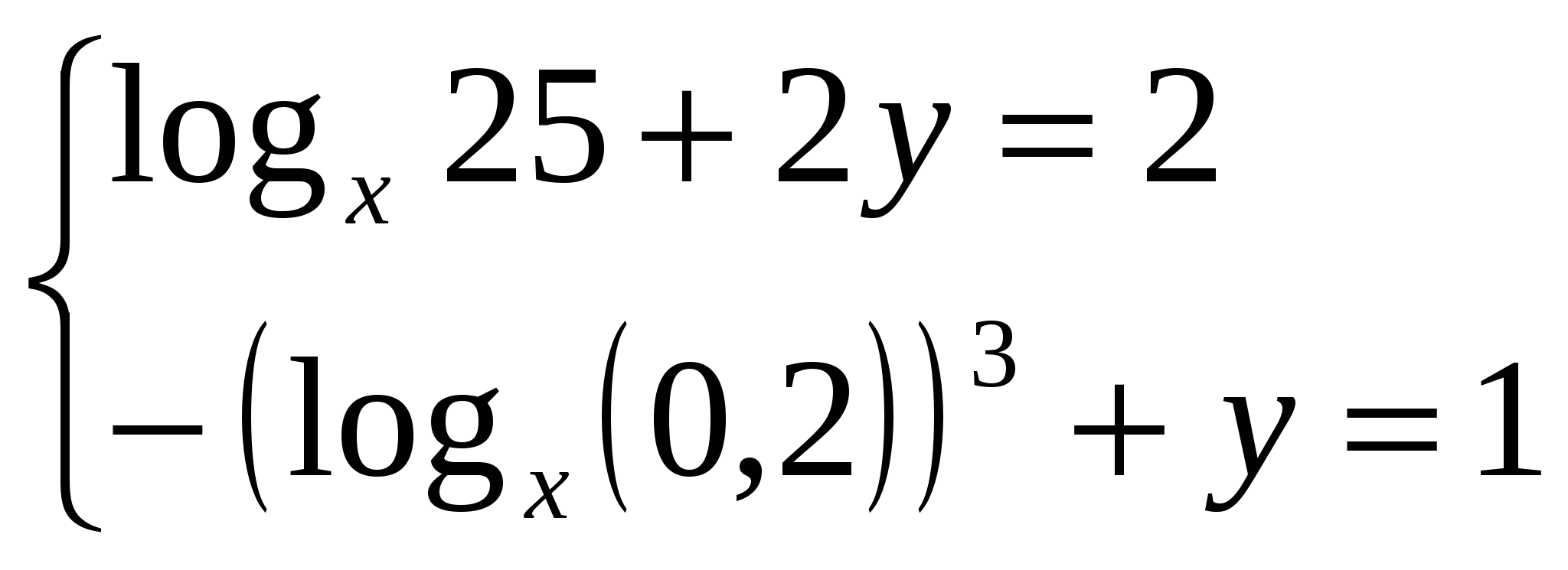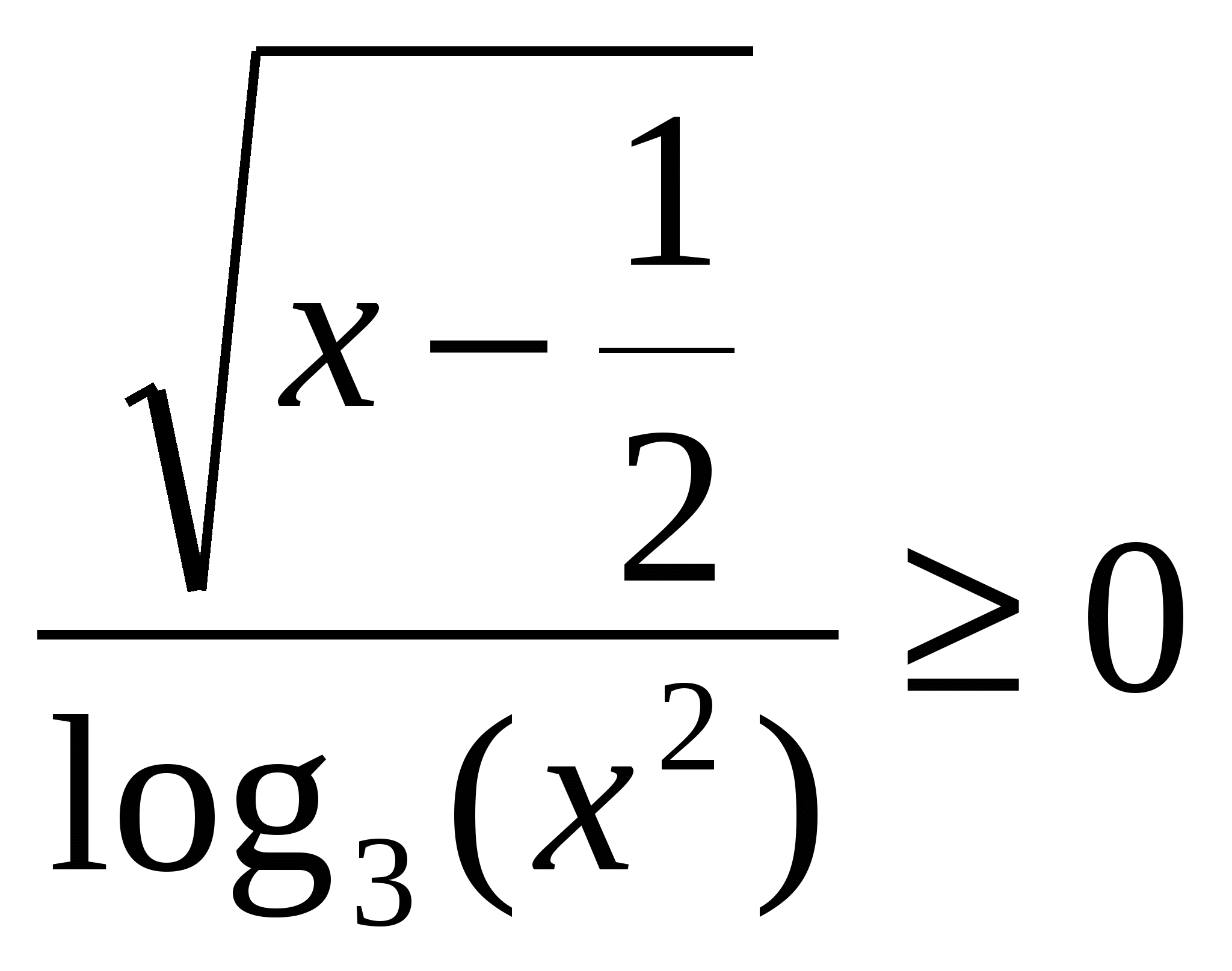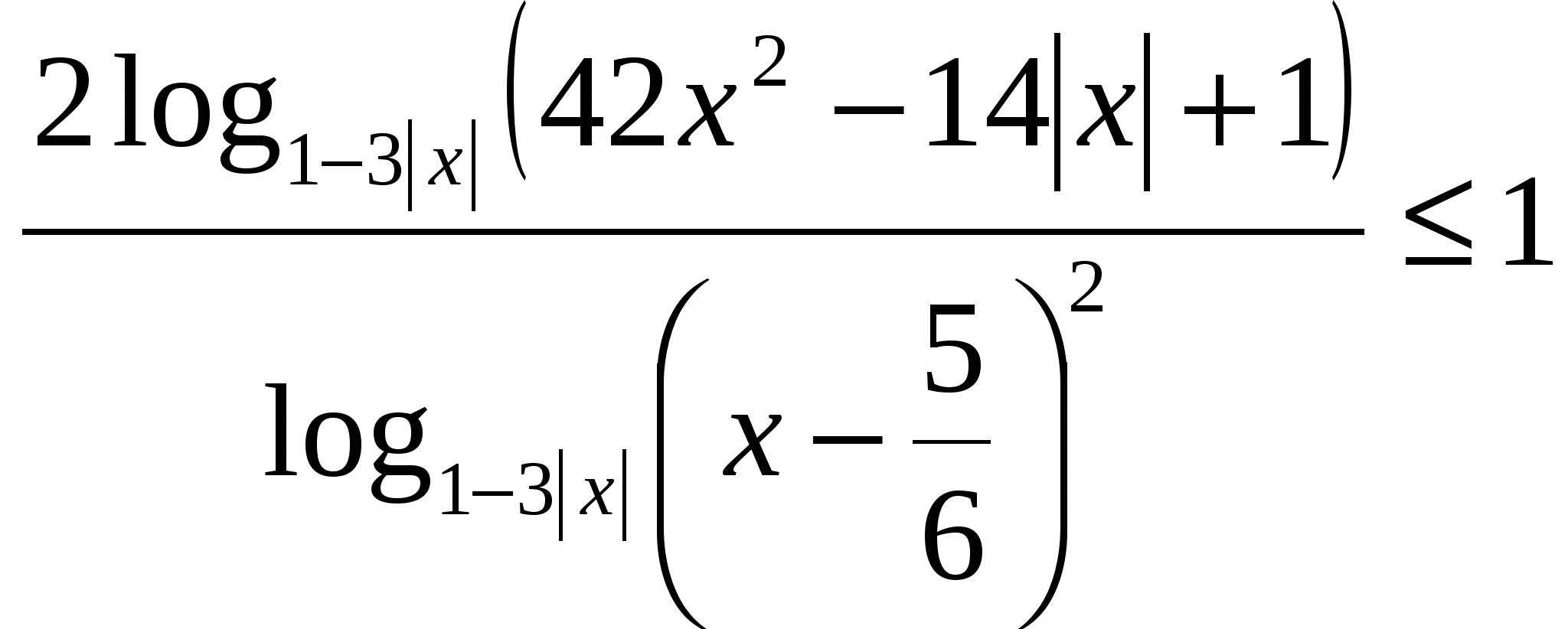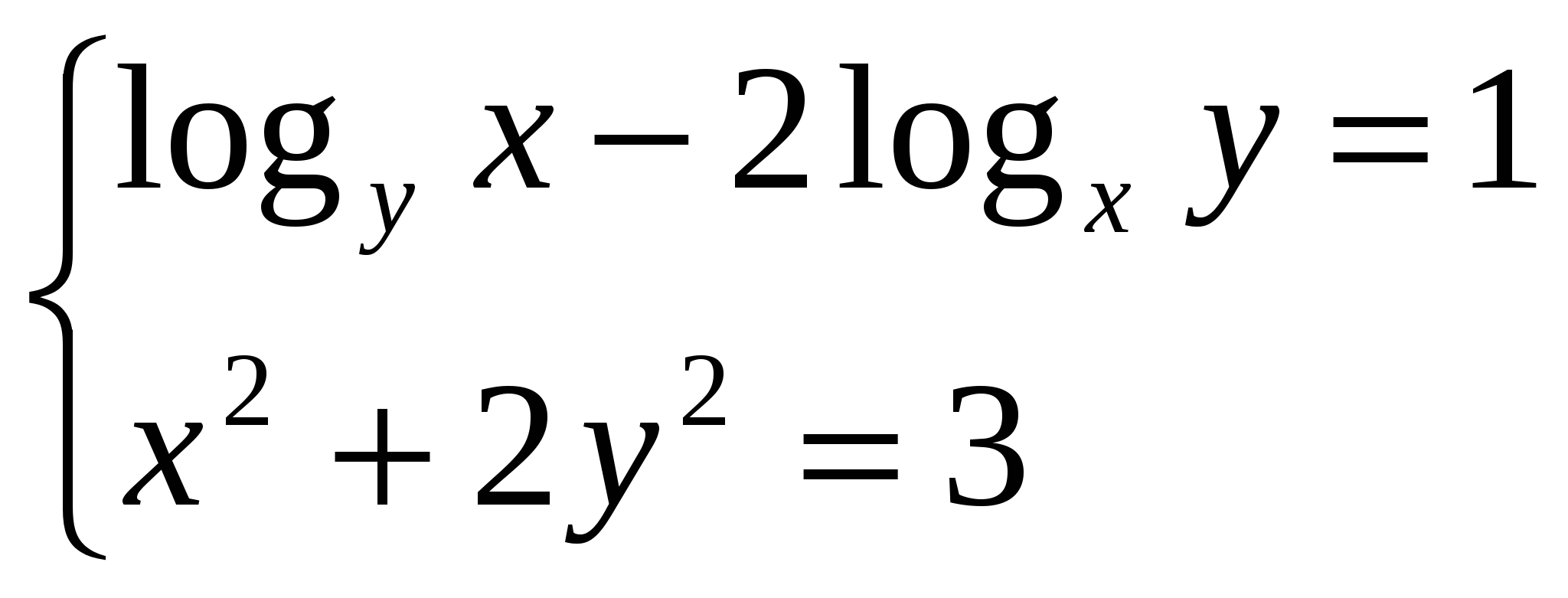Программа элективного курса для учащихся 11 класса «Решение уравнений и неравенств»
 Скачать 160.75 Kb. Скачать 160.75 Kb.
|
Авторская программа элективного курса для учащихся 11 класса «Решение уравнений и неравенств» (11 класс) Учитель математики высшей квалификационной категории Аксанова Ильсияр Исмагиловна МБОУ «Высокогорская средняя общеобразовательная школа №2 Высокогорского муниципального района Республики Татарстан» Пояснительная записка.Цели обучения математике в образовательной школе определяются её ролью в развитии общества в целом и формировании личности каждого отдельного человека. Практическая полезность математики обусловлена тем, что ее предметом являются фундаментальные структуры реального мира: пространственные формы и количественные отношения – от простейших, усваиваемых в непосредственном опыте людей, до достаточно сложных, необходимых для развития научных и технологических идей. Математическая подготовка играет значительную роль в общем образовании современного человека, особенно у выпускников профильных классов математического направления. Данный курс «Решение уравнений и неравенств» предназначен для учащихся 11 классов. В этом курсе рассматриваются простейшие уравнения и неравенства (уравнения и неравенства с модулями; рациональные уравнения и неравенства; уравнения и неравенства с радикалами) и более сложные (показательные; логарифмические; смешанные тригонометрические и содержащие одновременно логарифмы, модули, радикалы и т.п.). Таким образом, курс охватывает значительную часть математики, помогает сформировать у выпускников такие качества, как: умение грамотно выполнять алгоритмические предписания и инструкции;
Уравнения и неравенства применяют во многих областях науки, поэтому данный курс помогает анализировать и исследовать, применяя математические методы, процессы и явления в природе и обществе. Курс «Уравнения и неравенства» позволяет подготовить учащихся к ЕГЭ и вступительным экзаменам по математике, где часто предлагают задания на решение уравнений и неравенств. На изучение вопросов, представленных в программе отводится 35 часов, 1 час в неделю. Курс является предметно – ориентированным и рассчитан на учащихся, имеющих базовую математическую подготовку. Данный курс укрепляет и расширяет базовый уровень знаний учащихся за счет теоретического материала, помогающего в решении некоторых неравенств и уравнений, выходящего за рамки школьной программы и углубляет его через решение задач повышенной сложности. Цели курса:
Задачи:
Используемые технологии:
Для реализации целей и задач данного элективного курса предлагается использовать следующие формы занятий: лекции, беседы с элементами обсуждения, коллективное исследование поставленной проблемы и практикумы по решению основных типов задач, а также домашние контрольные работы учащихся с последующей совместной проверкой и самооценкой. Формой итогового контроля может стать тестовая работа, включающая разноуровневые задачи, рассмотренные на занятиях. Результат освоения курса считается положительным, если по итогам теста набрано более 32 баллов из 100 возможных. Требования к уровню освоения содержания курса: В результате изучения курса учащиеся овладевают следующими знаниями, умениями и способами деятельности:
Результатом освоения курса станет отработка у выпускников предметных знаний, умений и навыков, направленные на дальнейшее успешное изучение математики в ВУЗах. Ожидаемые результаты: Учащиеся должны знать, что такое уравнение, корень уравнения, равносильные уравнения, уравнения – следствия, посторонний корень, потерянный корень уравнения; уметь решать уравнения по видам и решать их предлагаемыми способами, выбирать более рациональный способ решения, если возможно одно и тоже уравнение решать различными способами. Содержание курса
Основное содержание курса1. Уравнения и неравенства с модулем (3 ч.) Уравнения с модулями. Раскрытие модулей - стандартные схемы. Метод интервалов при раскрытии модулей. Неравенства с модулями. Простейшие неравенства. Схемы освобождения от модулей в неравенствах. Эквивалентные замены разностей модулей в разложенных и дробных неравенствах («правило знаков»). Уравнения, содержащие модули. Систематизация различных видов уравнений и систем с модулем. Методы решения: раскрытие модуля исходя из определения; возведение обеих частей уравнения в квадрат; метод разбиения на промежутки; графический и аналитический способы решения уравнений и систем уравнений с модулем. Алгоритмы решения уравнений, содержащих модуль: решение линейных уравнений; решение квадратных уравнений; решение тригонометрических уравнений; решение показательных и логарифмических уравнений. Неравенства, содержащие модуль. Классификация различных типов неравенств с модулем и способы их решения. Алгоритмы решения неравенств, содержащих модуль. Графический и аналитический способы решения линейных неравенств и неравенств второй степени с модулем: неравенства, содержащие выражения ׀x׀; неравенства вида ׀ƒ(x)׀ >g(x) неравенства вида ׀ƒ1(x)׀±׀ƒ2(x)׀±…± ׀ƒn(x)׀> g(x). Системы неравенств, содержащие неизвестное под знаком модуля. Тригонометрические неравенства, содержащие неизвестное под знаком модуля. Показательные и логарифмические неравенства с модулем.
6. Смешанная тригонометрия. (4 ч.) Тригонометрические методы решения уравнений, методы решения уравнений с радикалами. Методы решения уравнений, содержащие модули.
Презентации проектов учащихся по решению уравнений и неравенств. 1. 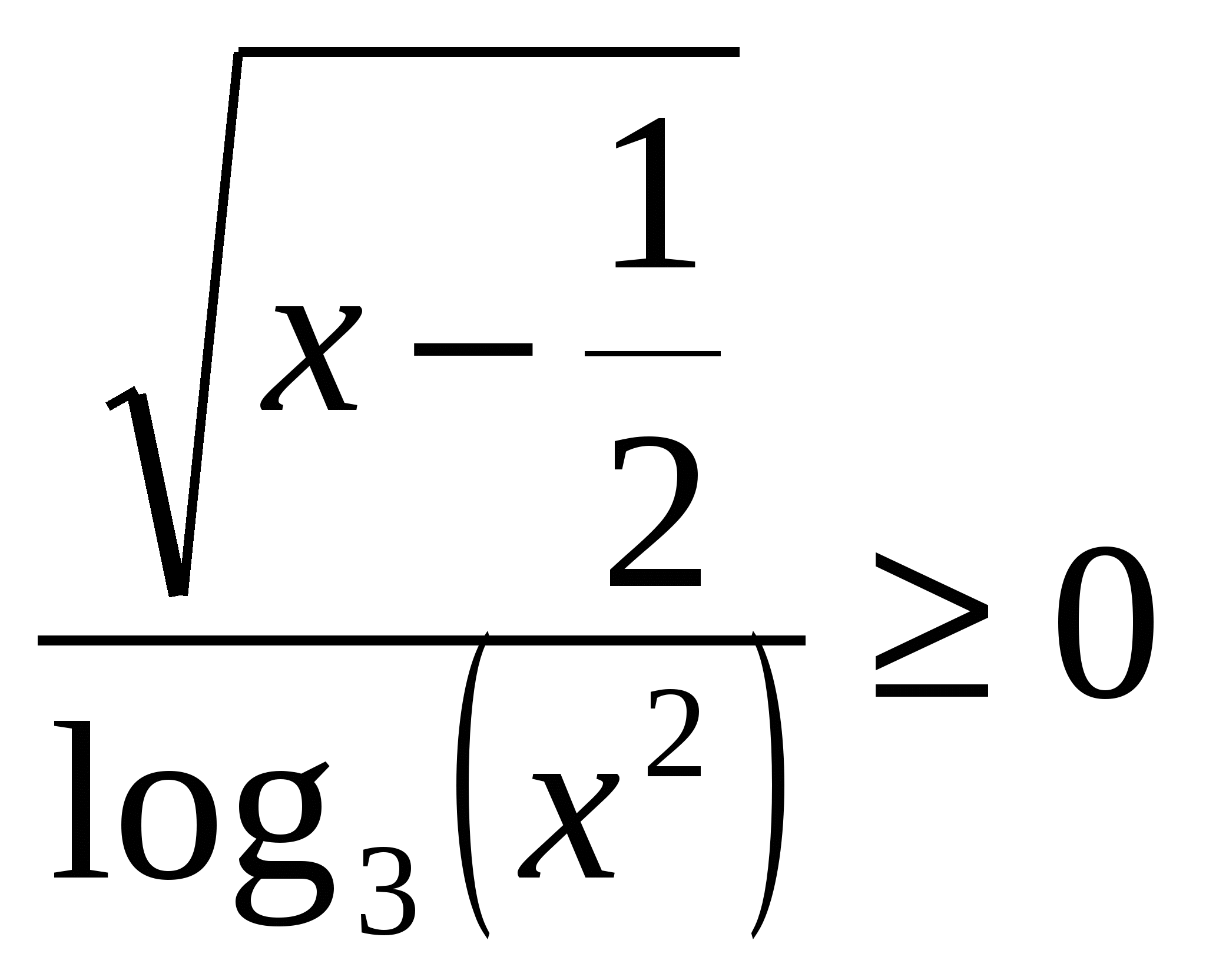 . .Решение. Рассмотрим два случая: 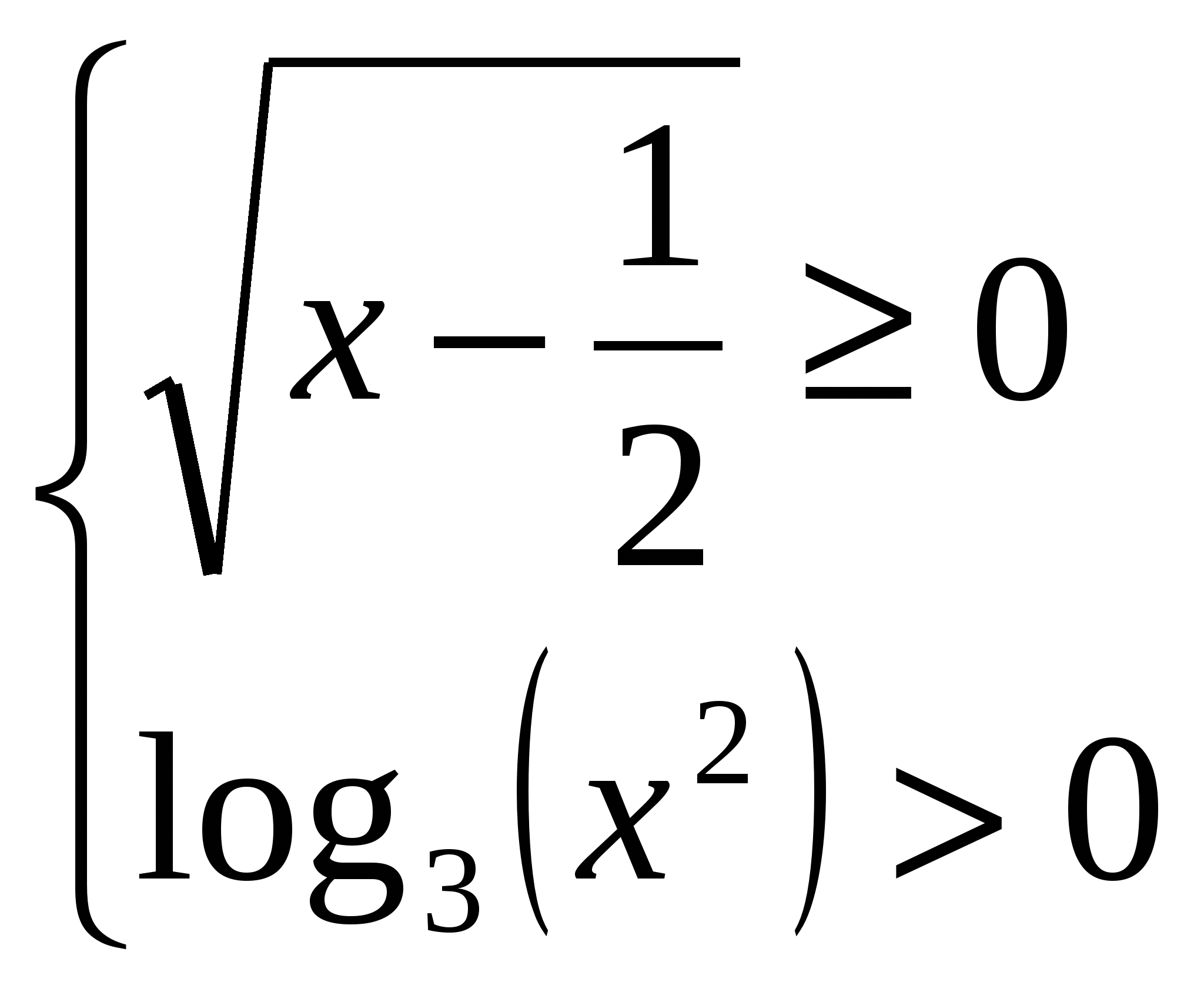 и и 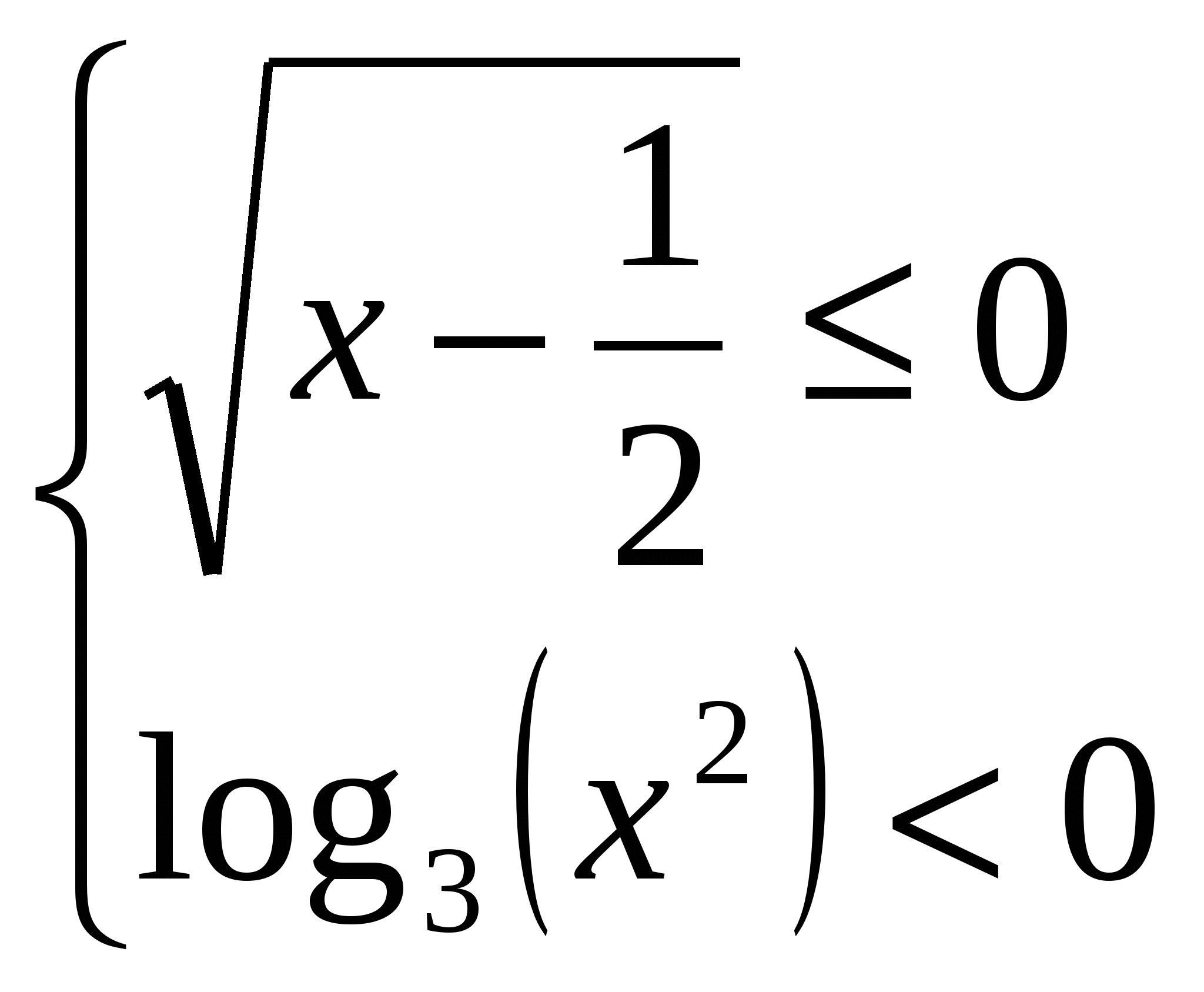 . .Первое неравенство первого случая выполняется при любых х из ОДЗ, т.е. при Первое неравенство второй системы выполняется только при Ответ: Задача 2. Решение. ОДЗ данного неравенства состоит из всех таких х, что В ОДЗ имеем 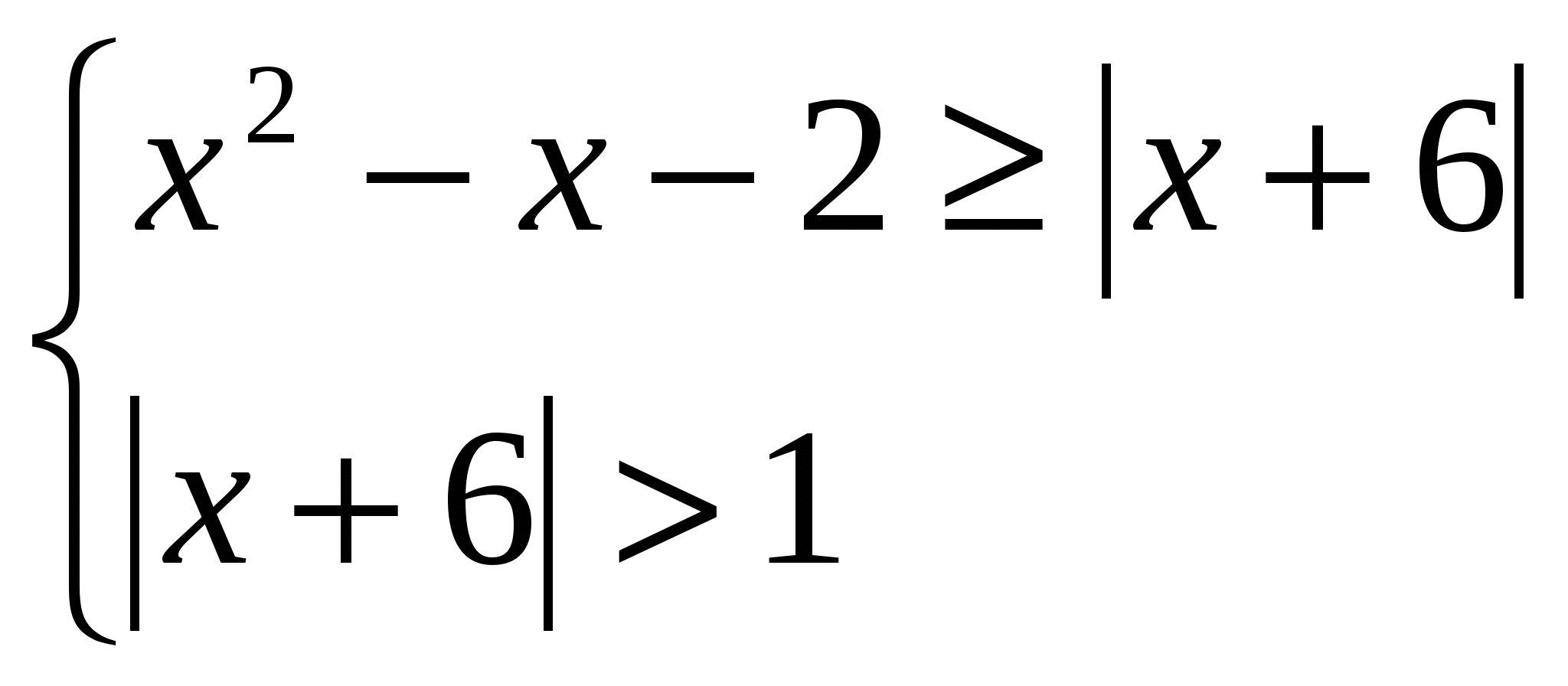 и и 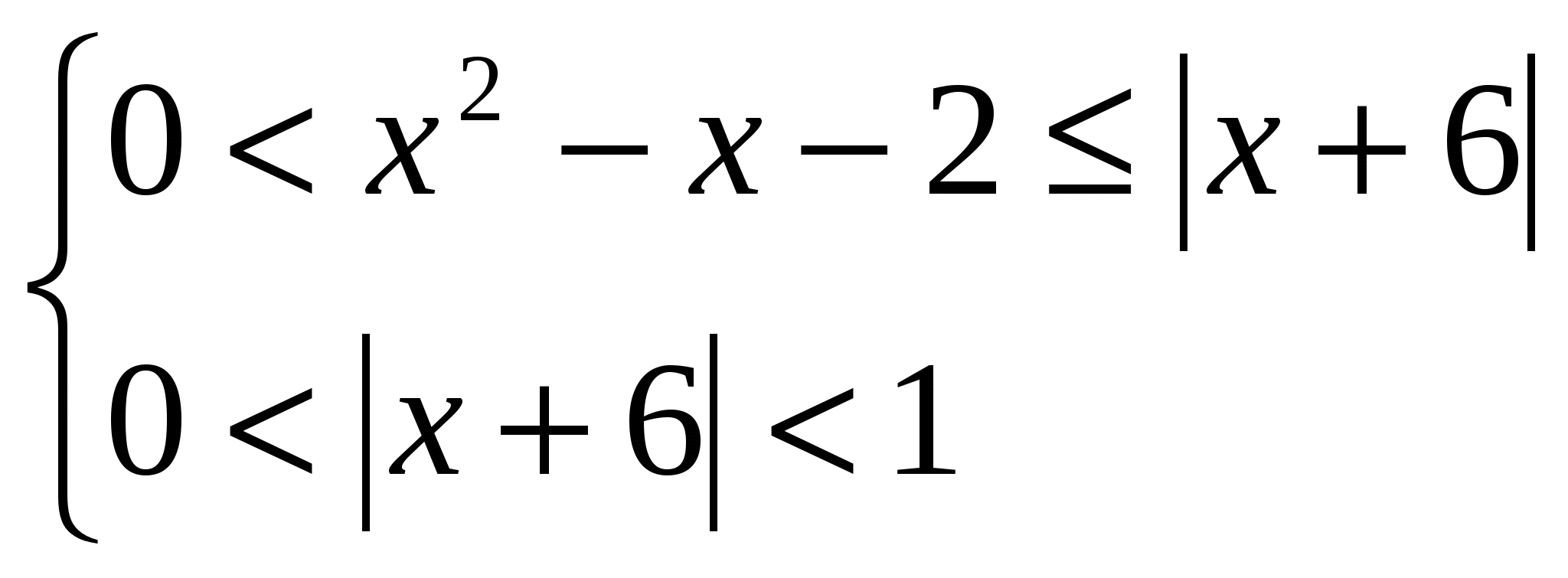 . .Решим первую систему. Если x > 6, то Если х < - 6 , то Вторая система решений не имеет. Ответ: Задача 3. 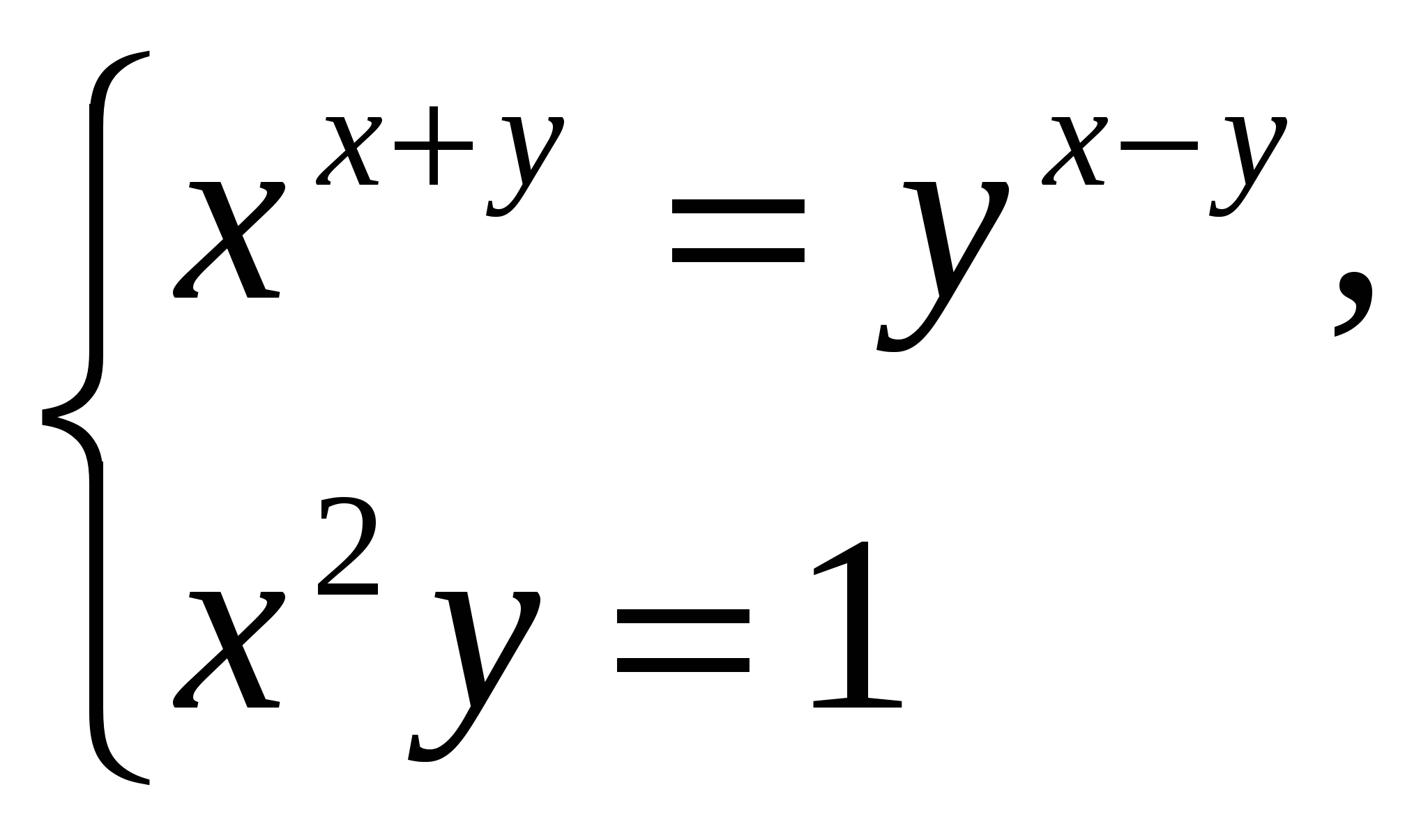 Решение. Второе уравнение системы эквивалентно тому, что Последнее уравнение эквивалентно тому, что либо х = 1, либо Ответ: 1, План-конспект занятия по теме «Уравнения с радикалами. Некоторые приёмы решения» Цели урока :
Тип урока :
Метод обучения :
Формы организации учебной деятельности :
План урока
а) на уровне воспроизведения, б) на уровне применения знаний. 5. Подведение итогов. Ход урока 1. Организационный момент. 2.Актуализация знаний. Вспомним а) определение и основные свойства корня n – ой степени, б) определение уравнения, что означает «решить уравнение». 3. Изучение новой темы : «Иррациональные уравнения. Некоторые приёмы решения». (лекция) а) Определение иррационального уравнения. б) Примеры : в) Что значит решить иррациональные уравнения ? Это значит : найти все такие значения переменной х, при которых уравнение превращается в верное равенство, либо доказать, что таких значений не существует. Другие понятия для иррациональных уравнений определяются так же, как и для рациональных уравнений. Широко распространёнными иррациональными уравнениями, предлагаемыми на вступительных экзаменах являются уравнения вида раические выражения, где неизвестная величина содержится под знаком корня и уравнения вида Вернёмся к уравнению вида Показывается способ решения уравнения данного вида : 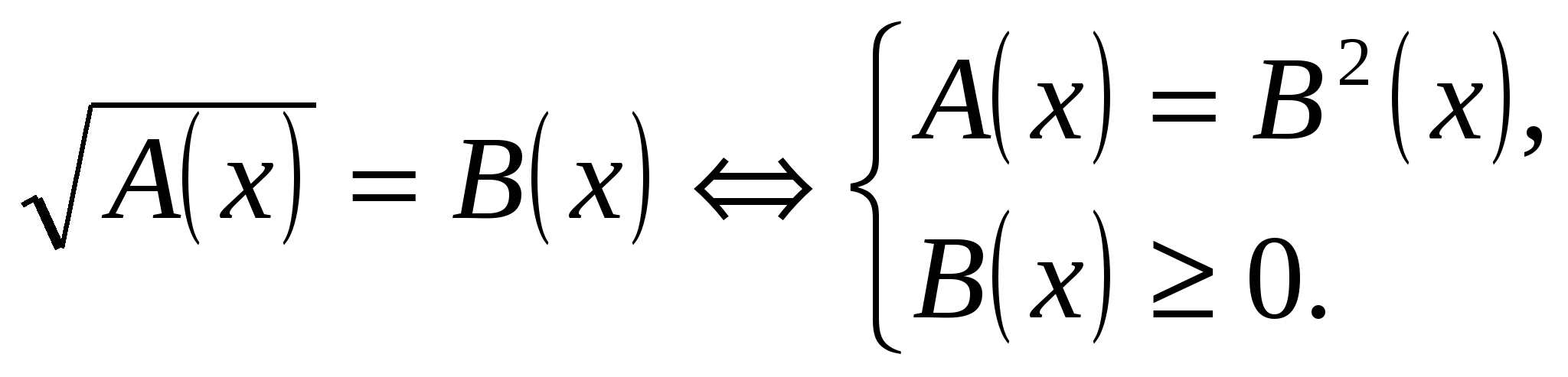 (1) (1)Примеры : 1) Учитель показывает решение этих двух уравнений на доске : Обратите внимание на правые части уравнений. Во втором уравнении должно налагаться дополнительное условие, которое вытекает из определения арифметического корня n – ой степени. Имеем 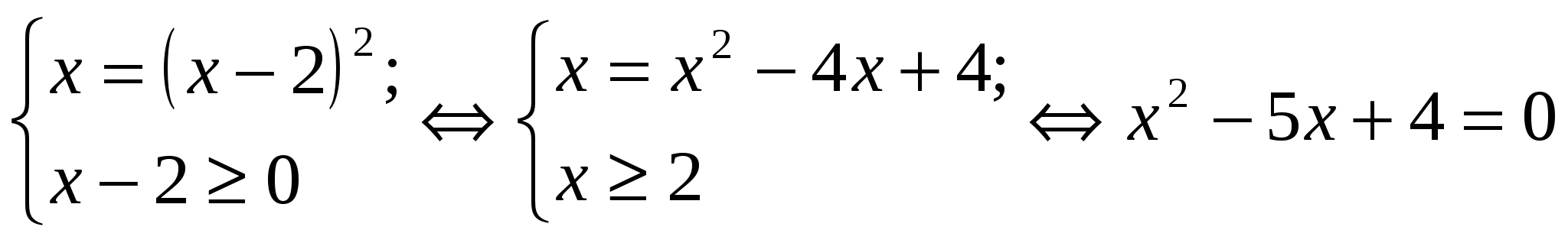 х1 = 4 , х2 = 1 – посторонний корень, не удовлетворяет условию х ? 2. Ещё один вид иррационального уравнения 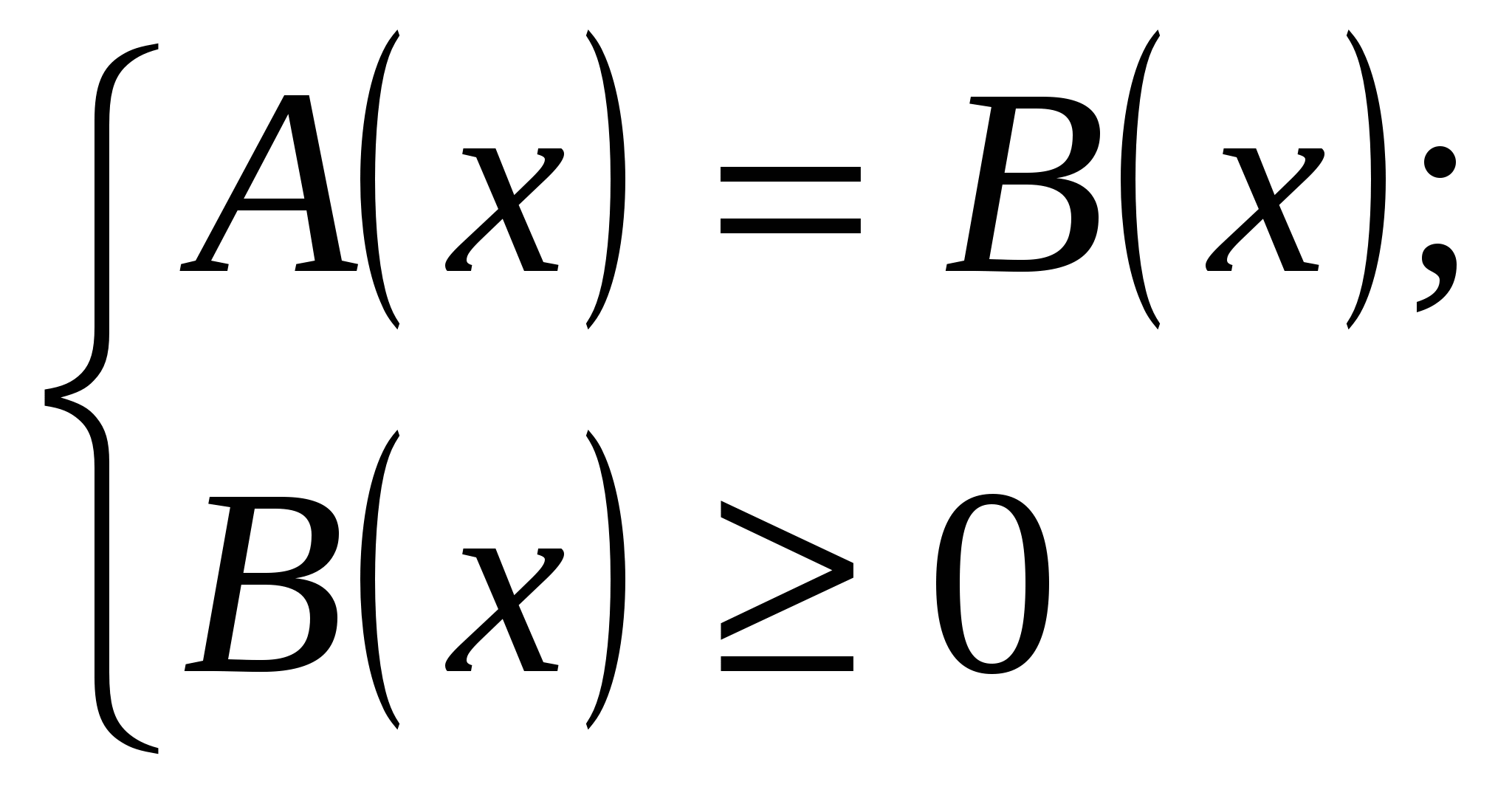 ( 2 ) ( 2 )Кстати, можно проверять и А (х) ? 0, т.е. то, что в данной задаче проще. Если уравнение не относится ни к одному из видов, то с помощью различных преобразований можно привести уравнения к Ι или ΙΙ виду. 0сновные методы решения иррациональных уравнений: Ι) Уединение радикала и возведение в степень. 1) Решить уравнение : 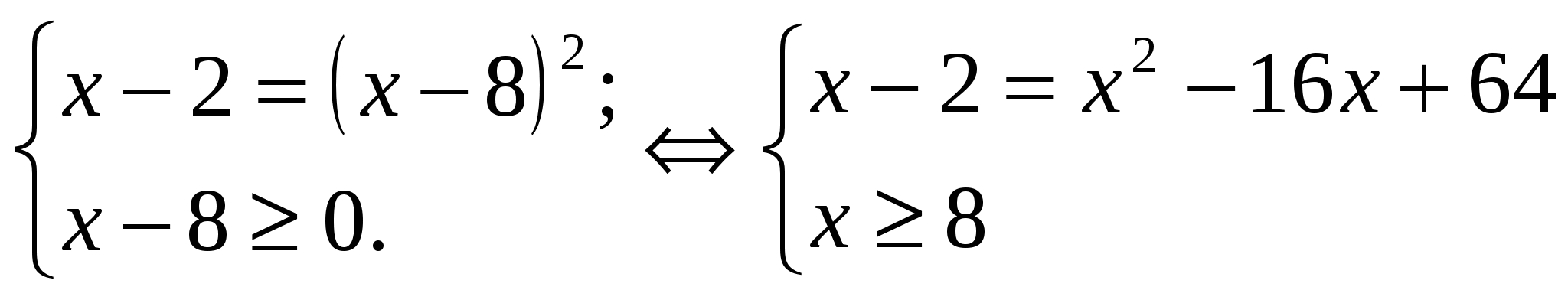 Рассмотрим уравнение системы х1 = 11, х2 = 6 – пост. корень, т.к. х ? 8. 2) Решить уравнение : Данное уравнение равносильно системе : 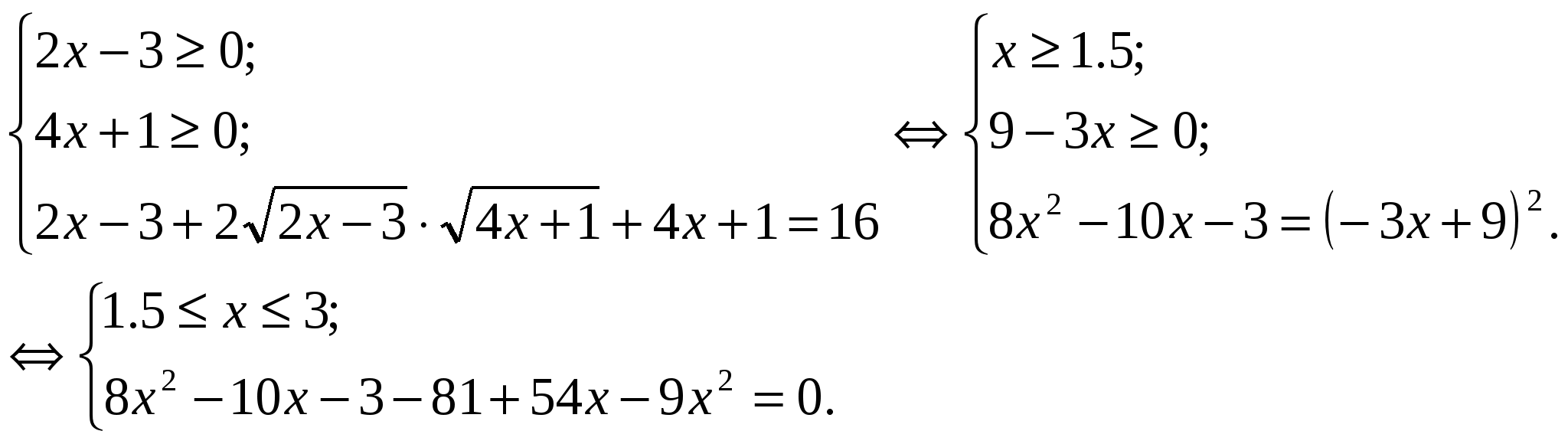 Решим второе уравнение системы : х1=2, х2=42 – посторонний корень. Ответ : 2. ΙΙ. Метод введения вспомогательного неизвестного. 1) Пусть Получим новое уравнение у1=2, у2=-6 – посторонний корень, т.к. у Вернёмся к замене 2) Решим уравнение : Пусть у1=-1 – посторонний корень, т.к. у>0, у2=2. Возвращаемся к подстановке Х=2,5. Уравнение дорешать дома. Часто этот метод встречается при решении других уравнений, не только иррациональных. ΙΙΙ. Нестандартный подход. 1) Пример : Пусть уравнение закончить дома. 2) Попробуйте решить: Решение : 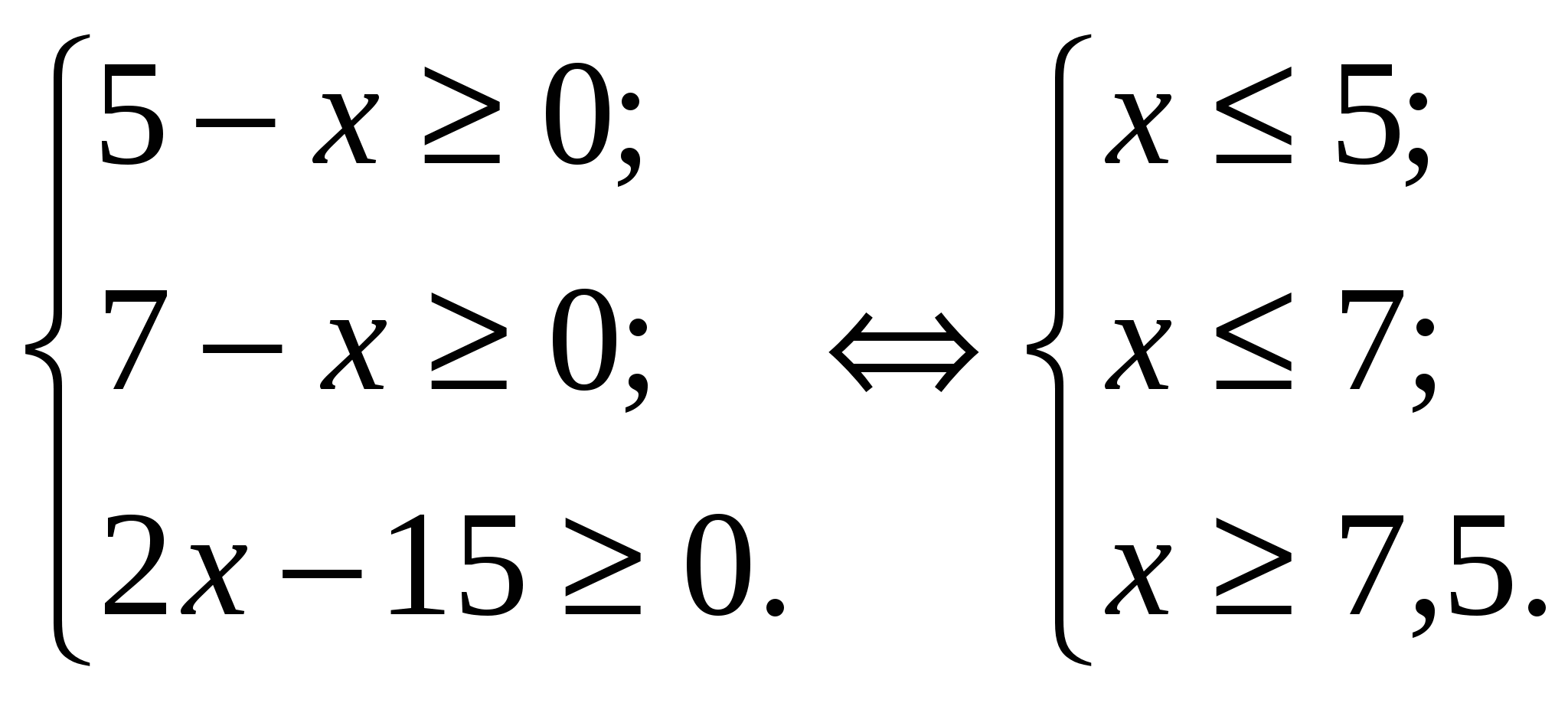 Ответ : нет решений. 3) Пример : Т.к. правая часть отрицательная, уравнение не имеет решения. Ответ : нет решения. 4.Закрепление Работа в парах и индивидуально.
Список использованной литературы:
2. В.В. Вавилов . Задачи по математике Уравнения и неравенства. М., «Просвещение», 2007 3. А.Г.Каспаржак «Элективные курсы в профильном обучении», М., НФПК, 2004. 4. М.К. Потапов и др. Нестандартные методы решения уравнений и неравенств. Москва, изд. МГУ, 2005. 5. В.В.Ткачук. Математика абитуриенту. Москва, изд. МЦНМО, 2006. 6. С. И. Колесникова. Решение сложных задач единого государственного экзамена. Москва, изд. АЙРИС ПРЕСС, 2006. |