Тема. Применение нестандартных способов при решении показательных и логарифмических уравнений

Название	Тема. Применение нестандартных способов при решении показательных и логарифмических уравнений
Дата	05.03.2016
Размер	63.68 Kb.
Тип	Урок

Тема. Применение нестандартных способов при решении

показательных и логарифмических уравнений

и неравенств.

Цель урока: 1) систематизировать знания о некоторых нестандартных

способах решения, умение применять свойства функций,

правила при решении уравнений и неравенств;

2) развивать умение видеть, умение распознавать

рациональность применения того или иного способа;

3) прививать интерес к математике, воспитывать

математическую грамотность ученика, как при устной,

так и при письменной работе.

Оборудование: компьютер, мультимедийный проектор, экран.

На доске:

План урока:

1. Орг. момент.

2. Устная работа.

3.Работа в группах

4. Защита решений.

5. Сам. работа.

6. Задание на дом

7. Итог урока.

Ход урока:

I. Организационный момент.

*знакомство с целью урока;

задачами, стоящими перед учениками в ходе уроке.

* использование при решении задач :

– монотонности функций;

– «правила знаков»;

– метода оценки;

– освобождение от логарифма.

II. Устная работа.

1. Какие из выражений имеют смысл?

а

)

а) да;

б

)

б) нет, т.к.

)

в) нет, т.к.

)

г) да;

д)

д) нет, т.к.

2. Решить уравнение:

(Корень уравнения угадываем: х = 1. Докажем, что других корней нет. Левая часть – сумма возрастающих функций есть функция возрастающая; правая часть – постоянное число. Следовательно, уравнение имеет одно решение.)

3. Решить уравнение:

/ :

( Корень уравнения угадываем: х = 2. Докажем, что других корней нет.

Разделим обе части уравнения на

следовательно, в левой части уравнения – сумма двух убывающих показательных функций, правая часть – const. Следовательно, уравнение имеет одно решение.)

– Какое свойство функций мы использовали при решении этих уравнений?

(свойство монотонности)
III. Работа в группах. Решение задач.

1 группа. Решить уравнение:

– Какой способ надо применить при решении данного уравнения?

Решение:

– Используем свойство монотонности убывающей функции, для этого

разделим на

– Можем ли мы угадать хоть один корень?

( Можно угадать корень уравнения: х = 2.)

– Докажем единственность.

В левой части – сумма убывающих функций, в правой части – const. Следовательно, левая и правая части имеют одну точку пересечения:

точка пересечения, х=2.

значит, уравнение имеет одно решение,

Ответ: х = 2.

2 группа. Решить неравенство:

– Применим теорему для функции f(f(x)).

– Сформулируем теорему:
Если функция у = f(x) – монотонно возрастающая функция, то уравнение

f(x)=x равносильно f(f(x)= x.

ОДЗ:

Решение:

– Выполним некоторые преобразования:

– вынесем в левой части за скобки 2, сократим:

– приведем к общему знаменателю:

– приведем подобные

т.к.

, а

, тогда

функция принимает вид

, где

- возрастающая функция, следовательно, по теореме имеем:

//////o o////// х

– Учитывая ОДЗ, получим:

Ответ: 1 ≤ x < 5, x > 10.

3 группа. Решить неравенство:

– Решим неравенство методом оценки левой и правой частей

;

Решение:

–Заметим, что

;

– Разделим обе части уравнения на положительное выражение

, получим:

;

– Выделим полный квадрат под радикалом и в показателе степени: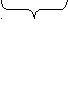

;

не меньше 1 не больше 1

– Левая часть неравенства не меньше 1, а правая часть не больше 1.

– Неравенство выполняется тогда и только тогда, когда обе части неравенства будут равны 1, а равенство достигается при х = 3.

Ответ: х = 3.

4группа. Решить уравнение:

;

Решение:

;

немонотонная ф-я немонотонная ф-я

– Решим уравнение методом оценки;

– Один корень уравнения можно легко угадать, это х = 1.

– Преобразуем логарифмы в левой части;

;

;

Выделим полный квадрат в правой части;

– Правая часть меньше или равна 1;

наибольшее значение правой части равно 1 при х=1;

– В левой части докажем, что выражение под знаком логарифма больше или равно 2: подведением под общую дробную черту, выделением полного квадрата

– левая часть достигает своего наименьшего значения, равного 1 при х = 1.

– Равенство выполняется тогда и только тогда, когда обе части уравнения равны 1, а это произойдет при х = 1.

Ответ: х = 1.

5 группа. Решить неравенство:

– Решим неравенство методом освобождения от логарифмов.

– Освободимся от логарифмов по правилу знаков:

Знак log a b совпадает со знаком произведения (а – 1)∙(в – 1).

Рассмотрим ОДЗ: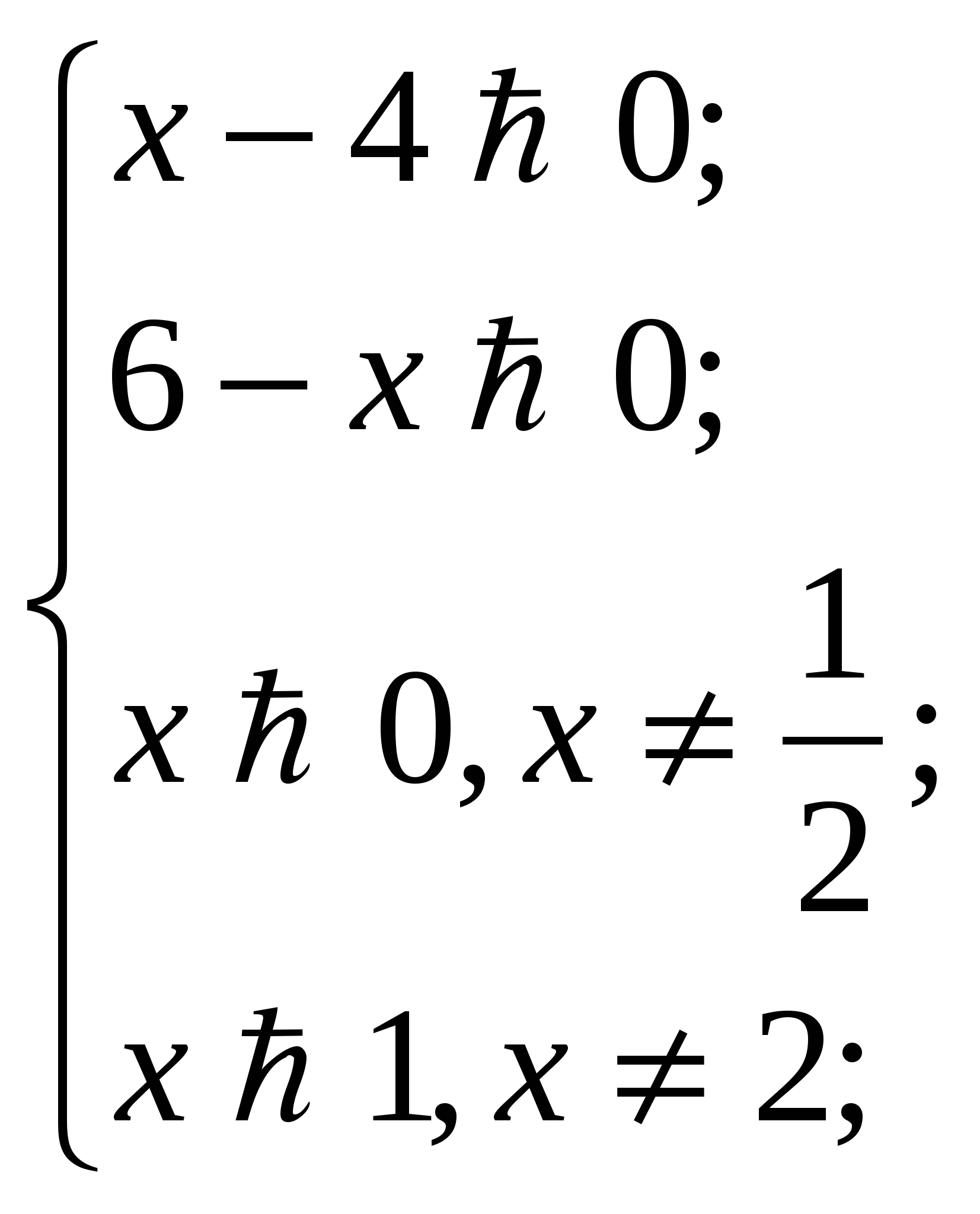

Решение:

– Т.к. нас интересует только знак левой части, то от можно логарифмов

освободиться по правилу знаков:

– Решим неравенство методом интервалов, рассмотрим функцию f(x):

айдем нули функции:

нули функции

+ +

//////o _ ο////////o////// х

½ 2 5

функция f(x) > 0 при

учитывая ОДЗ, получим:

Ответ:

IV. Защита проектов.

– От каждой группы выступает 1 человек с защитой своего решения (решение на доске кратко записать, пояснения по ходу решения, либо записать на ватмане).

V. Самостоятельная работа.

– Решить уравнение:

I вариант. II вариант.

– Проверим решение уравнений по готовым записям на доске:

I вариант.	II вариант.

Решение: при х=0 достигает унаим = 2 т.к. основание 0<0,1<1, то наибольшее значение равное 2 может быть при х = 0. Равенство возможно, когда обе части уравнения равны 2 при х = 0. Ответ:	Решение: выделим полный квадрат под знаком log: а Выделим полный квадрат в правой части: наименьшее значение равно 1 при Обе части одновременно будут равны 1 при Ответ:

– Оценить самостоятельно (оценка на полях).

VI. Задание на дом.

1). Решить уравнение:

2). Решить неравенство:

а)

б)

VII. Итог урока.

– Какие нестандартные способы решения мы использовали сегодня на уроке?

– Давайте посмотрим графические интерпретации этих способов.

На чем они основываются?

(Ответы: использование монотонности функции, использование правила знаков, метод оценки)