Применение производной в заданиях егэ, В8

Скачать 26.57 Kb. Название Применение производной в заданиях егэ, В8 Дата 12.02.2016 Размер 26.57 Kb. Тип Документы

Тема: Применение производной в заданиях ЕГЭ, В8. Знания и навыки учащихся: Знать угловой коэффициент прямой, геометрический смысл производной, достаточные условия возрастания и убывания функции, достаточные условия экстремума. I. Организационный момент. II. Устный опрос. В чем состоит геометрический смысл производной. Сформулируйте достаточные условия возрастания и убывания функции. Сформулировать достаточные условия экстремума функции. III. Теоретическая часть. Задания рассматриваются с помощью презентации и разбираются учителем. Задание 1. На рисунке изображен график производной. В какой точке отрезка [-5;0] функция достигает своего наименьшего значения? 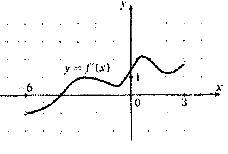Объяснение: так как на рисунке изображен график производной, а не функции(воспользуемся достаточными условиями возрастания и убывания функции), то наименьшее значение функции в точке рассматриваем на отрезке [-5;-4] там где она убывает. И достигает своего наименьшего значения в точке х = -4. 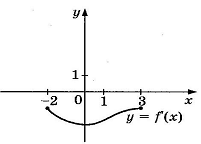Задание 2. Функция у = f(x) определена на отрезке [-2; 3]. На рисунке изображен график производной функции у = f'(x) .В какой точке отрезка функция принимает наименьшее значение? Объяснение: на рисунке изображен график производной. Воспользуемся достаточными условиями возрастания и убывания функции. На отрезке [-2;3] функция убывает, а значит, достигает своего наименьшего значения в точке х = 3. Задание 3. Функция у = f(x) определена на отрезке [-3; 5]. На рисунке изображен график производной функции у = f'(x). В какой точке отрезка функция принимает наибольшее значение? 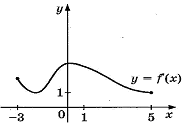Объяснение: на рисунке f'(x)>0 значит, функция возрастает и достигает своего наибольшего значения в точке х = 5. Задание 4. На рисунке изображен график производной. В какой точке отрезка [-1; 4] функция достигает своего наибольшего значения? 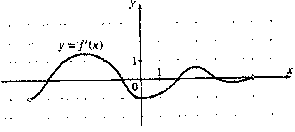Ответ: 4 Для закрепления данных примеров дается самостоятельная работа. (Приложение 1). 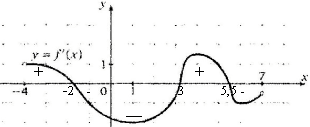Функция определена на отрезке [-4; 7]. На рисунке изображен график её производной у = f'(x). Найдите число точек максимума этой функции на интервале (-3,5; 6) Объяснения: воспользуемся достаточным условием максимума функции, (если f'(x) меняет знак с “+” на “–“ при переходе через точку х0, то х0 – точка максимума функции f (х)), то количество точек максимума 2 (х = -2 и х = 5, 5). Количество точек минимума 1 (х = 3). Для закрепления данного примера дается самостоятельная работа. (Приложение 2). На рисунке изображен график функции и касательная к нему в точке с абсциссой х0 . Найдите значение производной f'(x) в точке х0. 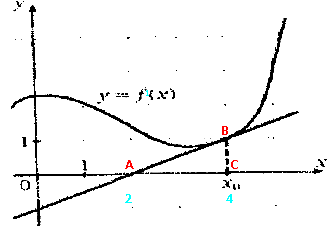Объяснение: для нахождения значения производной f'(x) в точке х0 воспользуемся геометрическим смыслом производной, f1(x0) = tgα = =1/2 = 0,5 В презентации рассмотрено ещё два примера. Для закрепления данных примеров дается самостоятельная работа. (Приложение 3). Ответы к приложениям: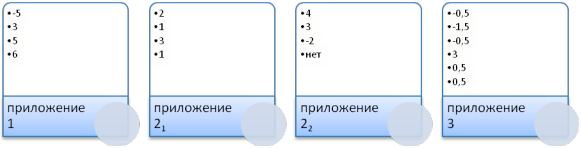