Применение нестандартных уроков в процессе обучения с целью развития творческих способностей учащихся
 Скачать 118.96 Kb. Скачать 118.96 Kb.
|
| Применение нестандартных уроков в процессе обучения с целью развития творческих способностей учащихся. Интерес к изучению математики во многом зависит от того, как проходят уроки. Даже на самых хороших уроках элемент обязательности сдерживает развитие увлеченности предметом. Поэтому на уроках я стараюсь применить нетрадиционные формы проведения уроков, веду поиск новых эффективных методов обучения и таких методических приемов, которые активизировали бы умственную деятельность учеников, стимулировали бы их к самостоятельному приобретению знаний. Стараюсь заботиться о том, чтобы на уроках каждый ученик работал активно и увлеченно, и использовать это как отправную точку для возникновения и развития любознательности. Особенно важно это в подростковом возрасте, когда формируются и определяются постоянные интересы и склонности к тому или иному предмету. И в этот момент надо раскрыть перед подростком притягательные стороны математики. Целью проведения нестандартных уроков является развитие творческих способностей учащихся, активизация умственной деятельности, формирование внутренних мотивов учения, закрепление базовых и получение новых знаний. Типы нетрадиционных уроков. - урок – КВН (урок-соревнование); - урок – деловая игра; - урок групповой работы (при подготовке к текущей контрольной работе); - урок – лабораторная работа (по геометрическому материалу в 5-6 классах); - урок – общественный смотр знаний; - урок – диспут (по геометрии «Красота и математика); - урок – лекция; - урок – семинар; - урок – зачет (как заключительный урок к большой теме); - урок – экскурсия («Геометрические тела и фигуры вокруг нас). Урок устной работы. Тема: «Виды уравнений и способы их решения» (9 класс). Цель: - обобщить и систематизировать знания учащихся по этой теме; - повторить теорию решения различных видов уравнений; - выработать умение определять вид уравнения; - научиться выбирать наиболее рациональный способ решения данного уравнения. Ход урока.
Дать историческую справку о том, что наука «алгебра» возникла в связи с решением разнообразных задач при помощи уравнений.
- Что называется уравнением? - Что значит решить уравнение? - Что называется корнем уравнения? - Какие существуют способы решения уравнений? - Какие виды уравнений существуют? - Как определить степень уравнения? - Каков общий вид линейного уравнения? Квадратного? -Дайте определение рационального, дробно-рационального уравнения, уравнения, содержащего корень. - Что называется областью определения уравнения? IV. Учащимся предлагается решить уравнения (устно, выполняя на бумаге только вычисления), объясняя, какого вида уравнения, способ решения каждого уравнения, теоретически обосновывая каждый шаг. Линейные уравнения. 1) 3х + 20(1-х)=35,2. 2) Квадратные и приводимые к квадратным. 1) х2-10=29. 2) 13= -х2 . 3) (х-4)2 – 5(х – 4)+6=0. 4) х4 – 13х2+36=0. 5) (х+2)4-11(х+2)2=12. Уравнения высших степеней. 1) х2=х3 2)3у5=96. 3) х3+ х2+ х +1=0. 4) 5,5m (m-1)(m+2,5)(m- Дробно-рациональные уравнения. 1) Иррациональные уравнения. 1) 2+ Уравнения с модулем. 1) │у+2│= Уравнения с параметром. 1) ах = 10. 2) 2а2х – 5=17. Самостоятельная работа с последующей проверкой. (Решить уравнения, фиксируя на листе только ответы). I вариант II вариант 1) а2- 6а+8=0 1) у2+ 5у+6=0 2)(х2-1)2 -11(х2-1)+24=0 2) (х2-2)2-9(х2-2)+14=0 3) х5+х4+в1=0 3) z7+z6+z+1=0 4) х2-14 5) 2х4=162 5) 4х2=128. V. Подведение итога. - Что повторили на уроке? - Какие виды уравнений существуют? - Какие способы решения уравнений существуют? Выставление оценок. Дается оценка устной работы (кто был активен)и оценка устной самостоятельной работы каждого ученика. Уроки обобщения и систематизации знаний проводятся, как правило, в конце темы, раздела, курса. Цели урока: Обучающая цель определяет основные моменты систематизации теории, наиболее сложные и трудные ее вопросы, расширение области применения знаний и их обобщение. Развивающая цель направлена на развитие у учащихся мыслительных операций: сравнения, сопоставления, абстрагирования, анализа, синтеза и др.; умение выделять главное, существенное в изученной теории, выстраивание учебного материала в сжатую с логической точки зрения структурную систему, установление связей между различными понятиями, фактами, разделами математики и другими учебными предметами. Воспитывающая цель данного типа урока состоит в том, что учитель не только должен дать знания по предмету, но и формировать математическую культуру учащихся, их духовные ценности. Уроки данного типа способствуют развитию индивидуальных качеств личности. Самостоятельности в суждениях, в выборе решений. Велика их роль и в формировании целостного восприятия изученной теории, науки и мировоззрения. Поэтому обобщение и систематизация математических знаний – один из факторов, влияющих на формирование культуры личности школьников. Урок обобщения и систематизации знаний по алгебре в 11 классе по теме: «Логарифмическая функция, свойства и график». Цель урока: - обобщение свойств логарифмической функции; - выделение понятия области определения и выявление существенных признаков этого понятия для логарифмической функции; - установление связей с наиболее трудными вопросами теории (решение неравенств методом интервалов, с модулем); - расширение класса функций, графики которых можно построить с помощью преобразований. I этап урока: Восприятие и воспроизведение повторяемого материала. Ведущие принципы дидактики: от простого к сложному и наглядность – являются основой этого этапа. Учащимся предлагается построить графики следующих функций: 1. у = Итак, каждая предложенная функция требует несложных преобразований, воспроизведения свойств логарифмической функции и выделения существенного свойства логарифмической функции – области определения. Это понятие является не только важным для построения графиков функций, но и основным для решения логарифмических уравнений и неравенств. Поэтому эти задания являются системой упражнений для обобщения данного понятии. Рассмотрим область определения каждой функции:
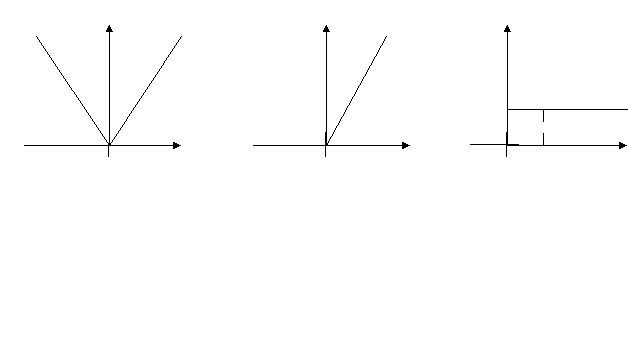 Рис.1 Рис.2 Рис.3 Таким образом, понятие области определения логарифмической функции поясняется наглядно. II этап урока. Систематизация, обобщение и осмысление изученного материала. Теперь учащиеся должны начать строить график функции с нахождения ее области определения. Задания, предлагаемые на этом этапе, требуют применения знаний из других разделов алгебры. Наиболее сложными являются неравенства с модулем. Следующие упражнения позволяют соединить знания учащихся, обобщить их умения и навыки. Построить графики функций: Найдем область определения первой функции, напомним, что 1. Если х≥0, то интервалов (рис.4) 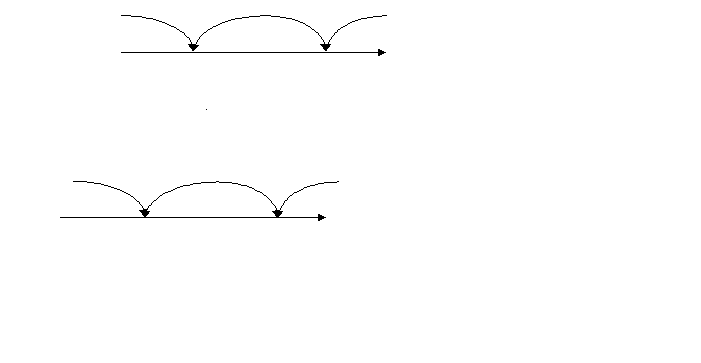 Откуда х Откуда х2. Если х‹0, то имеем (рис.5) На рис.5 показано решение этого неравенства. а при Найдем область определения второй функции, для чего решим неравенство:      (рис.6) Итак, После упрощения выражения под знаком модуля функция примет вид Построение графиков функций (1) и (2) является завершающим этапом обучения построения графиков с помощью преобразований и расширяет знания учащихся по данной теме. 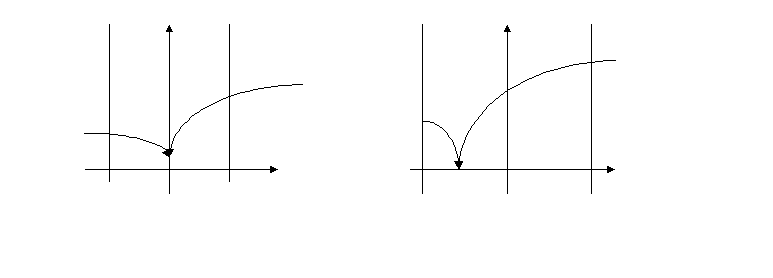 Рис.7 Рис.8 Ш этап урока. Расширение и углубление знаний. Построение графиков с помощью преобразований позволяет привести в систему все теоретические знания, и прежде всего умение строить графики функций с модулем. График функции Урок – диспут. «Что же такое красивая задача» (10 класс). Уроки – дискуссии дают возможность учащимся отказаться от шаблона, побуждают к творчеству, позволяют насладиться атмосферой свежих идей, получить удовольствие от учебного процесса. Я обратилась с вопросом к ученикам: А что же такое красивая задача? И уместно ли задачу наградить эпитетом «красивая»? В течение недели ученики думали над этим вопросом и подбирали примеры, подтверждающие их мнения. При выступлении первый ученик отметил, что красивые задачи в математике существуют, но их красоту могут ощутить только знатоки. Ему возразили, что красота понятна не только творцам, но и ценителям так же, как поэзия и музыка создаются художниками, прежде всего для людей. Другой ученик сказал, что, по его мнению, термин «красивая задача» применим лишь для тех задач, которые он смог решить сам; неудавшиеся попытки его угнетают, даже раздражают и формируют комплекс неполноценности. Третий ученик предложил продолжить спор после того, как они услышат решение следующей задачи. Плоскость покрыта квадратной решеткой. Можно ли через любой узел провести прямую, не проходящую больше ни через один узел решетки? 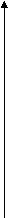  Решение. Р  ассмотрим декартову систему координат с началом отсчета в выбранной точке. Тогда все узлы решетки имеют целые координаты. Искомая прямая существует и их бесконечно много. ассмотрим декартову систему координат с началом отсчета в выбранной точке. Тогда все узлы решетки имеют целые координаты. Искомая прямая существует и их бесконечно много.Ученик подчеркнул, что класс не решал задачу, но она не оставила равнодушным никого. Задача понравилась всем. Но некоторые, признав ее красоту, пессимистически заявили, что они никогда не догадались бы до такого решения и это чувство немного притупляет их впечатление. Итак, вопрос о существовании красивых задач, как для творцов, так и для ценителей остался открытым. Чтобы изменить направление диспута, я задала классу вопрос: «Что определяет красоту рассмотренной задачи?». Ученик, предложивший ее, ответил, что он считает красивыми те задачи, решение которых основано на непредсказуемой идее. И другие согласились, оценивая красивую задачу как источник не предполагаемых и неожиданных идей. На доске появилась формула: КРАСИВАЯ ЗАДАЧА = НЕПРЕДСКАЗУЕМОСТЬ + НЕОЖИДАННОСТЬ + НЕПРЕДПОЛАГАЕМОСТЬ. (*) Ученица предложила включить в формулу «нестандартность», но большинство отвергли это, сказав, что эта характеристика слишком «стандартна» для оценки такого качества, как красота. После появления формулы многие учащиеся признались, что, подбирая к уроку задачи, они только сейчас могут объяснить свой выбор. Одна ученица предложила заменить левую часть формулы (*) на «оригинальная задача». Свое предложение она аргументировала тем, что словарь русского языка С.И. Ожегова раскрывает понятие красоты как совокупность качеств, доставляющих наслаждение взору и слуху, и, следовательно, термин «красивая задача» не уместен. Спор разгорелся с новой силой, многие сказали, что «красота может доставлять удовольствие не только слуху и взору, но и разуму!..». И в качестве примера была предложена следующая задача.  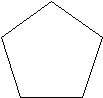 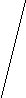    При пересечении диагоналей правильного пятиугольника в свою очередь образуется правильный пятиугольник. Существуют ли пятиугольники, отличные от правильного, диагонали которого при пересечении образуют пятиугольник, подобный данному. При пересечении диагоналей правильного пятиугольника в свою очередь образуется правильный пятиугольник. Существуют ли пятиугольники, отличные от правильного, диагонали которого при пересечении образуют пятиугольник, подобный данному.Решение. Искомым пятиугольником является параллельная проекция правильного пятиугольника. Действительно, изображения подобных фигур, лежащих в параллельных плоскостях, подобны. (Это легко доказать, пользуясь определением преобразования подобия и свойствами параллельного пректирования). Эта задача многих удивила. И я убедилась, что задача и ее решение могут оказывать сильное эмоциональное воздействие на детей. Вокруг возник спор. Один ученик предложил усложнить условие, рассмотрев, например, правильный десятиугольник, и тем самым сделать решение эффектней. Некоторые возразили, что, решая исходную задачу, прибегали к средствам планиметрии, а это выгодно подчеркивало красоту решения. Прервав спор, один ученик выразил свое отношение к красивым задачам. В его понимании к ним относятся и такие, которые при первом знакомстве поражают своей сложностью и даже вызывают страх, а решение их удивительно изящное и простое. И он предложил свою задачу. Отрезок длины l разделили на n отрезков. На каждом из них, как на диаметрах, построили полуокружность. Эту же операцию повторили, разделив данный отрезок на k частей. Найти отношение суммы длин полуокружностей первого и второго разбиений.  Решение. Пустьd1,d2, …dn – длины отрезков первого разбиения, d1`, d2`,…dk` - длины отрезков второго разбиения. Сумма длин полуокружностей в первом случае S1= После решения этой задачи формула (*) дополнилась еще одним слагаемым «УДИВИТЕЛЬНАЯ ПРОСТОТА». Эмоциональный накал диспута возрастал. Некоторые настаивали на том, чтобы в формуле было еще одно слагаемое «простота» как противовес псевдосложности условия, все рассмотренные задачи относятся к красивым и потому, что они обладают доступными решениями. Одной неожиданности недостаточно, так, например, ехать из Киева в Москву через Париж – предложение неожиданное, но пока непростое. Этот пример убедил учащихся расширить формулу. Один учащийся предложил в (*) включить слагаемое «фантазия», рассказав известную задачу П.Дирака о рыбаках. [Камышко И. « Поль Дирак и задача о трех рыбаках» Квант, 1982, №9.] Одна ученица сказала: «К красивым задачам я отношу те задачи, для решения которых надо сделать решительный, революционный шаг». И предложила задачу. Найти закономерность в построении последовательности: 111, 213, 141, 516, 171, 819, 202, 122, … Решение. Решение действительно революционное: надо в данной последовательности иначе расставить запятые, и мы получим 11, 12, 13, 14,… Формула (*) пополнилась новым компонентом «РЕВОЛЮЦИОННЫЙ ШАГ». Еще один ученик дополнил (*) слагаемым «УДИВЛЕНИЕ», предложив задачу. Бактерии размножаются делением. За 1 сек. из одной бактерии образуются две. Одна бактерия вместе со своим потомством заполняет пробирку за 1 час. За какое время эту же пробирку заполнят две бактерии? Решение. Из 1 бактерии за 1 сек. образуются 2. Дальше процесс в пробирке с одной бактерией идет точно также, как и в пробирке с двумя бактериями. Следовательно, ответом будет 59мин. 59сек. (А не 30 мин., как высказались некоторые). То есть, есть задачи, в которых верный ответ в корне отличается от интуитивно предполагаемого. Это разительное отличие, вызывая удивление, украшает задачу. В конце диспута две ученицы высказали следующие суждения: - Первая упрекнула своих товарищей в том, что они не замечают красоту, лежащую на поверхности, например, теорему Пифагора. Эту теорему она считает простой, неожиданной и удивительной. И назвала еще: признак делимости на 3 и на 9; теорема Виета; геометрический смысл производной; свойство медиан треугольника; теорему синусов и др. - Вторая вернула нас к началу дискуссии. Отметив свое признание существования красивых задач независимо то ее участия в их решении, заострила внимание на том, что ценить красоту в математике могут лишь те, кому нравится эта наука, а нравиться она может лишь тем, кто награждается успехом при решении задач. Она предложила включить в (*) слагаемое «УВЕРЕННОСТЬ В БУДУЩЕМ УСПЕХЕ», или «ОПТИМИЗМ», а в конце поставить знак «+» и многоточие. Подводя итоги диспута, я обратила внимание класса на то, что восприятие красоты (не только в науке, а и в любом виде человеческой деятельности) требует от человека определенного труда на приближение к уровню компетентности, который заложил автор в свое произведение, будь то математическая теорема, картина, музыкальный опус или эффективно работающее техническое устройство. Итак, на доске возникла формула: КРАСИВАЯ ЗАДАЧА = НЕПРЕДСКАЗУЕМОСТЬ + НЕОЖИДАННОСТЬ + УДИВИТЕЛЬНАЯ ПРОСТОТА + ПРОСТОТА + ФАНТАЗИЯ + РЕВОЛЮЦИОННЫЙ ШАГ + УДИВЛЕНИЕ + ОПТИМИЗМ + ТРУД + … |