«Комбинаторика и элементы теории вероятностей и статистики в задачах гиа»
 Скачать 112.22 Kb.
|
| Выступление учителя математики гимназии «Дмитров» Сергеевой Ирины Анатольевны по теме «Комбинаторика и элементы теории вероятностей и статистики в задачах ГИА» Цели: подобрать материал по теме «Комбинаторика и элементы теории вероятностей и статистики в задачах ГИА» при итогово-тематическом повторении за курс 7-9 классов Задачи: систематизировать теоретический материал по комбинаторике, теории вероятностей и статистике; разобрать задачи по данной теме; подобрать задачи для самопроверки. Глава 1 Комбинаторика – это область математики, изучающая вопросы о числе различных комбинаций (удовлетворяющих различным условиям), которые можно составить из данных элементов. Основные понятия и формулы
Свойства сочетаний без повторений: Комбинаторный принцип умножения если одну часть действия можно выполнить k способами, а другую – p способами, то все действие можно выполнить kp числом способов. Комбинаторный принцип сложения. Если два действия взаимно исключают друг друга, и одно из них можно выполнить k способами, а другое – p способами, то оба действия можно выполнить k+p числом способов. Группа А Задача 1. Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра в числе встречается один раз? Решение: Из четырех цифр можно получить P4 перестановок. Из них надо исключить те перестановки, которые начинаются с нуля. Таких перестановок P3. Тогда: P4 – P3 =4! - 3! = 18 Ответ: 18 четырехзначных чисел Задача 2. Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, 3? Решение: На первое место можно поставить цифры 1, 2, 3(3 способа), на второе, третье и четвертое место – 0,1,2,3 (4 способа). Применяя комбинаторный принцип умножения получим 3  444 = 192 числа ( 2 способ: 3 =343=192) Задача 3. Сколько различных перестановок можно составить из букв слова АБАКАН? Решение. Требуется найти число перестановок на множестве из 6 элементов, среди которых три элемента одинаковы:  .Задача 4. Сколько перестановок можно получить из букв слова КОЛОКОЛА? Решение. Требуется найти число перестановок с повторениями на множестве из 8 букв, среди которых: буква К повторяется 2 раза; буква О повторяется 3 раза; буква Л повторяется 2 раза буква А повторяется 1 раз. Таким образом,  .Задача 4. В секции занимается 8 человек. Сколькими способами можно составить команду из 4 человек? Решение:  способовЗадача 5. В секции занимается 8 человек. Сколькими способами можно составить команду из 4 человек, один из которых бежит 100м, второй – прыгает в длину, третий – стреляет, четвертый – метает копье? Решение:  способовЗадача 5.В кондитерском магазине продаются три сорта пирожных: наполеоны, эклеры и бисквитные. Сколькими способами можно купить 9 пирожных? Решение: Здесь требуется найти число всевозможных комбинаций из 9 элементов, которые можно составить из данных 3 элементов, причем эти элементы в каждой комбинации могут повторяться, а сами комбинации отличаются друг от друга хотя бы одним элементом. Значит, речь идет об отыскании числа сочетаний с повторениями из 3 элементов по 9. Значит,  способовЗадача 6. Сколько различных звукосочетаний можно взять на 10 выбранных клавишах рояля, если каждое звукосочетание может содержать от трех до десяти звуков? Решение: Для каждого звукосочетания клавиши нажимаются одновременно, и с учетом комбинаторного правила сложения, получим  Задача 7. Сколькими способами можно расположить на шахматной доске две ладьи так, чтобы одна не могла взять другую? (Одна ладья может взять другую, если она находится с ней на одной горизонтали или на одной вертикали шахматной доски) Решение: Первую ладью можно поставить на любое из 64 полей. При этом 14 полей оказываются под угрозой, значит, для второй ладьи остается любое из 64 -15 = 49 полей. Значит, общее число вариантов 64 49 = 3136Группа Б Задача 8. Тридцать человек разбиты на три группы по 10 человек в каждой группе. Сколько может быть различных составов групп? Решение: первую группу можно составить  способами, вторую  способами, третью  способами. С учетом комбинаторного правила умножения число всех составов групп  Задача 9. Сколько четырехзначных чисел, составленных из цифр 0, 1, 2, 3, 4, 5, содержат цифру 3 (цифры в числах не повторяются)? Решение: Всего можно составить  четырехзначных чисел, включая и те, которые начинаются с цифры 0. Исключив их, получим  . Теперь из этого набора нужно исключить все четырехзначные числа, не содержащие цифру 3, т.е. состоящие из цифр 0, 1, 2,4,5.аналогично получим  Значит,  числаЗадача 10. На книжной полке помещается 30 томов. Сколькими способами их можно расставить так, чтобы при этом первый и второй тома не стояли рядом? Решение: Всего на полке можно сделать  перестановок. Убрав первый том, получим 29! перестановок книг. Первый том можно поставить рядом со вторым двумя способами 2 29! (вычтем их). Таким образом,  способамиЗадача 11. Найти число диагоналей n-угольника Решение: Имеется n точек на плоскости. Всего можно провести  отрезков. Исключим n отрезков, которые являются сторонами многоугольника. Значит, всего диагоналей будет  .Задача12. В скольких точках пересекаются диагонали выпуклого n-угольника, если никакие три из них не пересекаются в одной точке? Решение: Одна точка пересечения диагоналей возникает за счет двух диагоналей, т.е.четырех вершин. Их можно выбрать:  Задача 13. Восемь авторов должны написать книгу из 16 глав. Сколькими способами возможно распределение материала между авторами, если два человека напишут по три главы, четыре – по две, два – по одной главе книги? Решение: Искомое число таково  способамиЗадача 14. У одного мальчика 6 значков, а у другого – 5. Сколькими способами они могут обменять 2 значка одного на 2 значка другого? Решение: Найдем сколькими способами каждый выдерет из своих значков по 2 для обмена:  ;  . Используя комбинаторное правило умножения получим 1015=150 способовГлава 2 Теория вероятностей – это раздел математики, в котором изучаются закономерности случайных событий Случайным событием называется событие, которое при осуществлении некоторых условий может произойти или не произойти. Событие называется достоверным, если в результате испытания оно обязательно происходит. Невозможным называется событие, которое в результате испытания произойти не может. Случайные события называются несовместными в данном испытании, если никакие два из них не могут появиться вместе. Вероятностью события A называют отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможных несовместных элементарных исходов, образующих полную группу  Свойство 1. Вероятность достоверного события равна единице Свойство 2. Вероятность невозможного события равна нулю. Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей. Итак, вероятность любого события удовлетворяет двойному неравенству  .Вероятность появления хотя бы одного из двух несовместных событий равна сумме вероятностей этих событий: P(C) = P(A) + P(B) Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий: P(C) = P(A) P(B)Вероятность противоположного события  : P() = 1 – P(A)Задача 1. В урне 10 шаров: 6 белых и 4 черных. Вынули два шара. Какова вероятность, что оба шара белые? Решение. Вынуть два шара из десяти можно следующим числом способов:  . Число случаев, когда среди этих двух шаров будут два белых, равно  . Искомая вероятность  .Задача 2. В кабинете работают 6 мужчин и 4 женщины. Для переезда наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц три женщины. Решение. Общее число возможных исходов равно числу способов, которыми можно отобрать 7 человек из 10, т.е.  .Найдем число исходов, благоприятствующих интересующему нас событию: трех женщин можно выбрать из четырех  способами; при этом остальные четыре человека должны быть мужчинами, их можно отобрать  способами. Следовательно, число благоприятствующих исходов равно  .Искомая вероятность 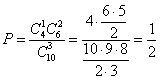 .Задача 3. Бросают два игральных кубика. Найдите вероятность того, что в сумме выпадет четное число очков, не превосходящее шести. Решение: Общее число исходов 6 6 = 36. Благоприятных исходов 9: (1;1),(1;3), (2;2), (3;1), (1;5), (2;4), (3;3), (4;2), (5;1). Значит, P =  Задача 4. В контрольной по математике 5 задач с выбором ответа. К каждой задаче предлагается 4 ответа, один из которых верный. За четыре верно решенные задачи ученик получает оценку 4. Какова вероятность получить 4, если случайным образом отметить верные ответы? Решение: Так как к каждой задаче предлагается 4 варианта ответов, то общее число возможных комбинаций ответов равно 45 = 1024. Благоприятными исходами являются  . Значит, искомая вероятность P =  Задача 5. В мешочке лежат неразличимые на ощупь карточки с буквами К, О, С, М, О, С. Какова вероятность того, что, наудачу извлекая карточки и выкладывая их на столе, получится слово КОСМОС? Решение: Занумеруем карточки числами от 1 до 6: К1 О2 С3 М4 О5 С6. Общее число исходов равно количеству перестановок P6 = 6! Благоприятными исходами будут следующие: К1 О2 С3 М 4О5 С6 , К1 О2 С6 М 4О5 С3, К1 О5 С3 М 4О2 С6 , К1 О5 С6 М 4О2С3. Искомая вероятность равна P=  Задача 6. В окружность вписан правильный треугольник. Найти вероятность того, что точка, брошенная в круг, попадет в треугольник. Решение: Пусть радиус окружности равен R, тогда сторона треугольника R  . Тогда площади фигур равны: Sтр = ; Sокр=  . Таким образом , искомая вероятность равна P =  0,41  Глава 3 Математическая статистика – это дисциплина, разрабатывающая математические методы систематизации и использования статистических данных для научных и практических выводов Статистические характеристики Мода – значение признака, имеющее наибольшую частоту в статистическом ряду распределения. Среднее арифметическое (среднее) – это сумма всех чисел ряда, деленная на их количество. Медиана – это такое значение признака, которое разделяет упорядоченный ряд на две равные части. Если в ряду нечетное количество чисел, то это число, стоящее посередине ряда, если – четное, то среднее арифметическое двух средних по счету чисел. Размах ряда – это разность наибольшего и наименьшего чисел упорядоченного ряда Задача 1. Измеряя рост семи пришедших на урок учеников, учитель физкультуры получил ряд чисел: 152, 148, 152,154, 158,148, 152.Найдите разность между модой и медианой того ряда. Решение: Упорядочим ряд 148, 148, 152,152, 152,154, 158. Мода ряда – 152. Медиана – 152. Значит,152 – 152 =0 Задача 2. Дима в четверти получил по 10 предметам среднюю оценку 4,2.По какому количеству предметов он должен улучшить оценку на 1 балл, чтобы его средняя оценка стала 5? Решение: Сумма набранных баллов по всем предметам S= x1+x2+x3+…+x10= 4,2 10=42.Тогда сумма баллов, набранная после исправления S1= y1+y2+…+y10=5 10=50. Следовательно, Дима должен улучшить свой результат на S-S1=50-42=8 баллов. Значит, он должен улучшить на 1 балл по 8 предметам.Задача 3. При каких значениях x медиана ряда чисел 1, 2, 3, 4, x будет равна 3? Решение: После ранжирования данного ряда чисел в зависимости от значений x будет получен один из следующих рядов: x, 1, 2, 3, 4, если x<1 1, x, 2, 3, 4, если 1<=x<2 1, 2, x, 3, 4, если 2<=x<3 1, 2, 3, x, 4, если 3<=x<4 1, 2, 3, 4, x, если x>4 Найдем для каждого из этих рядов его медиану: 2, 2, x, 3, 3. Получаем, что медиана равна 3 при x>=3. З Глава 4 Задачи для самостоятельного решения
Ответы: 1. 124; 2. 2520; 3. 1/5; 4. 0,92; 5. 6010; 6. 2/9; 7. 67/315; 8. 98/9900 Используемая литература:
|
