Наименование раздела
|
Название темы
|
Содержание учебного материала
|
Требования к уровню подготовки учащихся
|
Действительные числа.
|
1. Натуральные и целые числа.
|
Делимость натуральных чисел. Признаки делимости. Простые и составные числа. Деление с остатком. НОД. НОК.
|
Знать/ понимать:
- натуральные, целые, рациональные, иррациональные числа;
- модуль числа; множества;
- признаки делимости;
- простые и составные числа.
Уметь:
- выполнять арифметические действия с действительными числами;
- применять понятия, связанные с делимостью целых чисел, при решении задач;
- решать уравнения и неравенства с модулями;
- избавляться от иррациональности в знаменателях дробей.
|
2. Рациональные числа.
|
Перевод бесконечной периодической десятичной дроби в обыкновенную.
|
3. Иррациональные числа.
|
Понятие иррационального числа.
|
4. Множество действительных чисел.
|
Действительные числа. Числовая прямая. Числовые неравенства.. Числовые промежутки. Аксиоматика действительных чисел.
|
5. Модуль действительного числа.
|
Определение модуля действительного числа и его свойства.
|
6. Метод математической индукции.
|
Формулировка принципа математической индукции.
|
Контрольная работа № 1.
|
|
Уметь применять изученный теоретический материал при выполнении письменной работы.
|
Числовые функции.
|
7. Определение числовой функции и способы ее задания.
|
Функции. Область определения и множество значений. График функции. Построение графиков функций, заданных различными способами.
|
Знать/ понимать:
- числовые функции, способы задания функций;
- свойства числовых функций;
- периодическая функция;
- обратные функции.
Уметь:
- определять значения функции по значению аргумента при различных способах задания функции;
- строить графики изученных функций, выполнять преобразования графиков;
- описывать по графику поведение и свойства функций;
- решать уравнения используя их графические представления.
|
8. Свойства функций.
|
Свойства функций: монотонность, четность и нечетность, выпуклость, ограниченность, непрерывность. Графическая интерпретация.
|
9. Периодические функции.
|
Определение периодической функции.
|
10. Обратные функции.
|
Взаимно обратные функции. Область определения и область значений обратной функции. График обратной функции. Нахождение функции, обратной данной.
|
Контрольная работа № 2.
|
|
Уметь применять изученный теоретический материал при выполнении письменной работы.
|
Тригонометрические функции.
|
11. Числовая окружность.
|
Числовая окружность. Макеты числовой окружности и работа с ними.
|
Знать/ понимать:
- числовая окружность, синус, косинус, тангенс и котангенс числового аргумента;
- синус, косинус, тангенс и котангенс углового аргумента;
- радианная мера угла;
- основные тождества;
- соотношения между градусной и радианной мерами угла.
Уметь:
- находить на окружности точки по заданным координатам;
- находить координаты точки, расположенной на числовой окружности;
- решать простейшие тригонометрические уравнения с помощью числовой окружности;
- преобразовывать тригонометрические выражения с помощью тождеств;
- строить графики основных тригонометрических функций и преобразовывать их;
- описывать свойства тригонометрических функций;
- преобразовывать выражения, содержащие обратные тригонометрические функции.
|
12. Числовая окружность на координатной плоскости.
|
Координаты точек числовой окружности. Составление таблицы координат точек числовой окружности.
|
13. Синус и косинус. Тангенс и котангенс.
|
Синус, косинус, тангенс, котангенс произвольного угла.
|
14. Тригонометрические функции числового аргумента.
|
Основные тригонометрические формулы.
|
15. Тригонометрические функции углового аргумента.
|
Радианная мера угла.
|
16. Функции 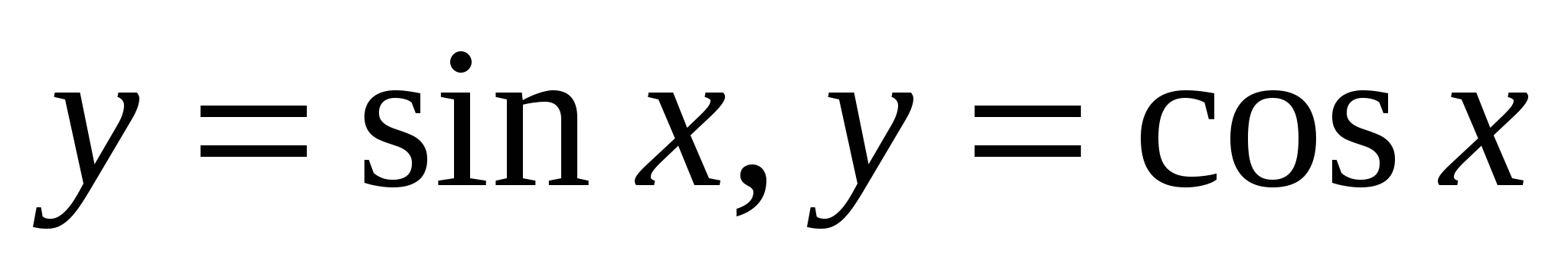 , их свойства и графики. , их свойства и графики.
|
Построение графиков функций 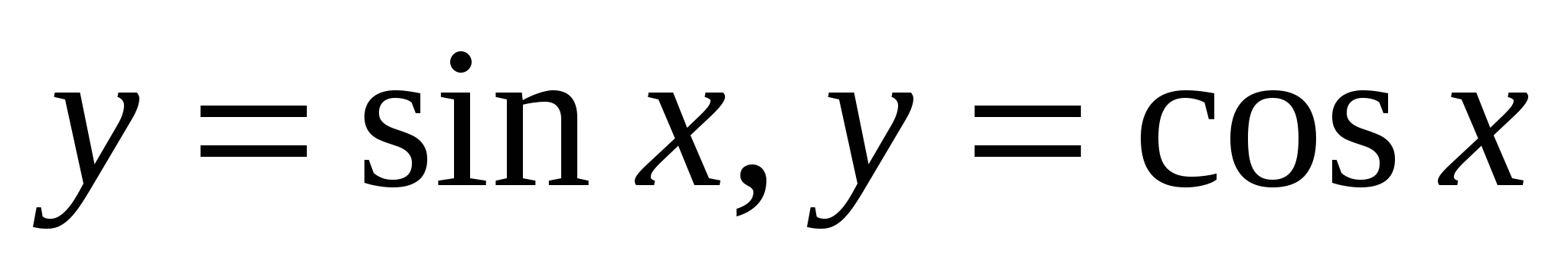 и работа с ними. и работа с ними.
|
17. Построение графика функции 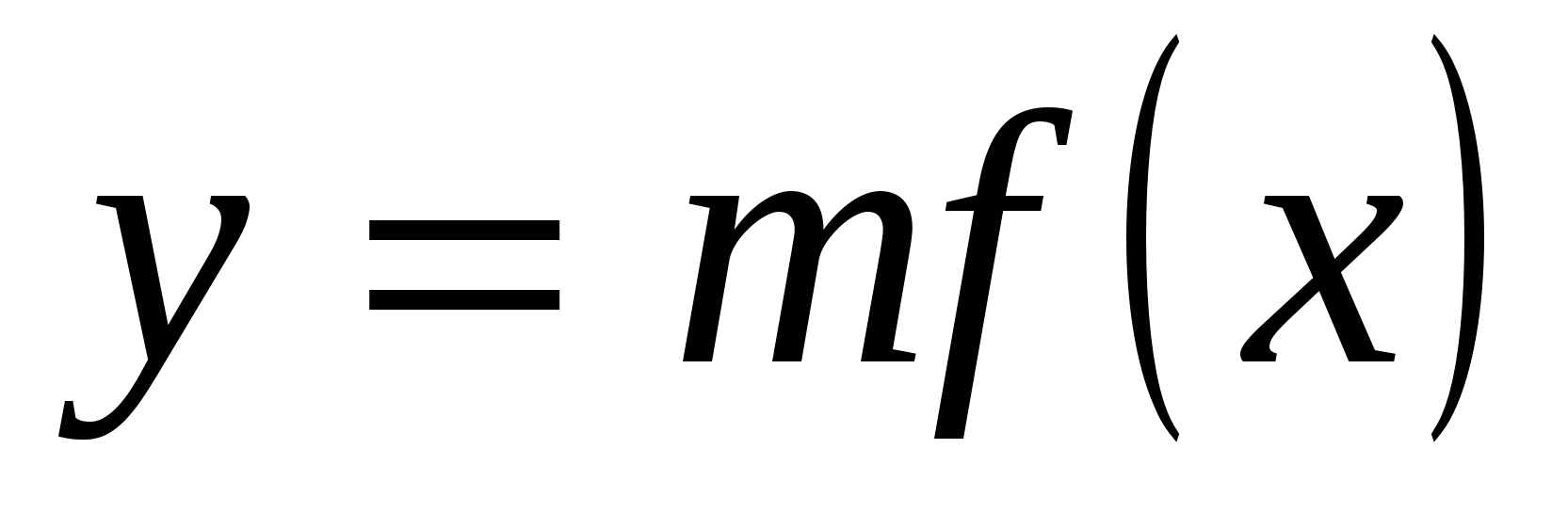 . .
|
Построение графика функции 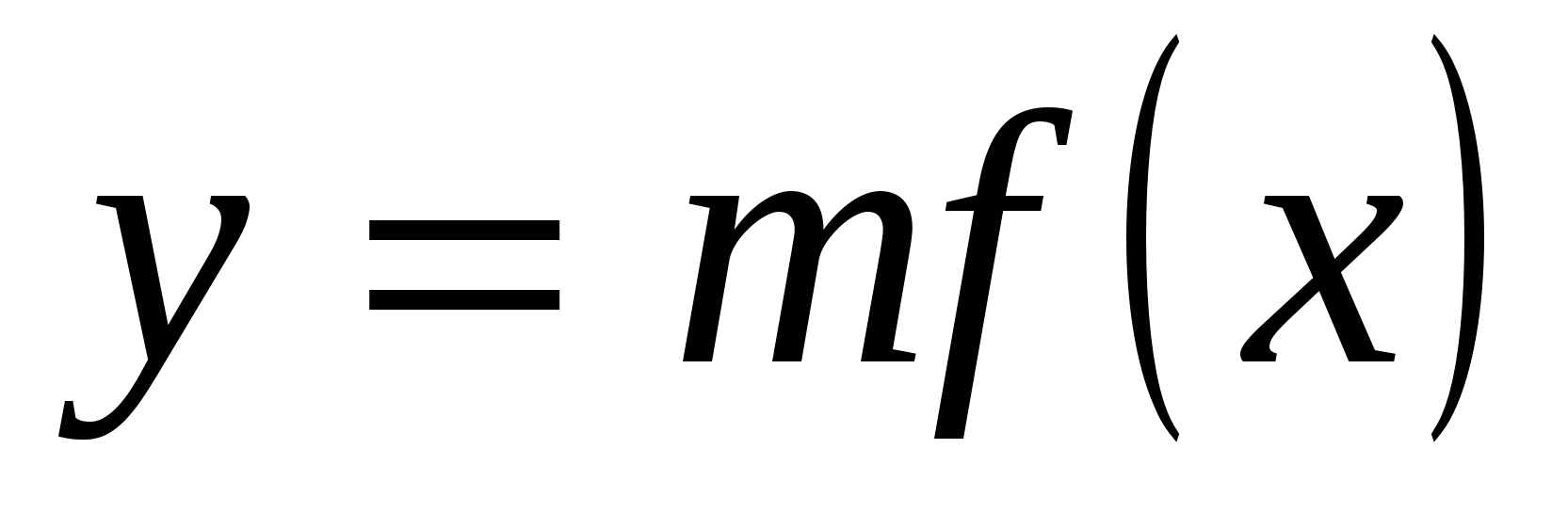 . .
|
18. Построение графика функции 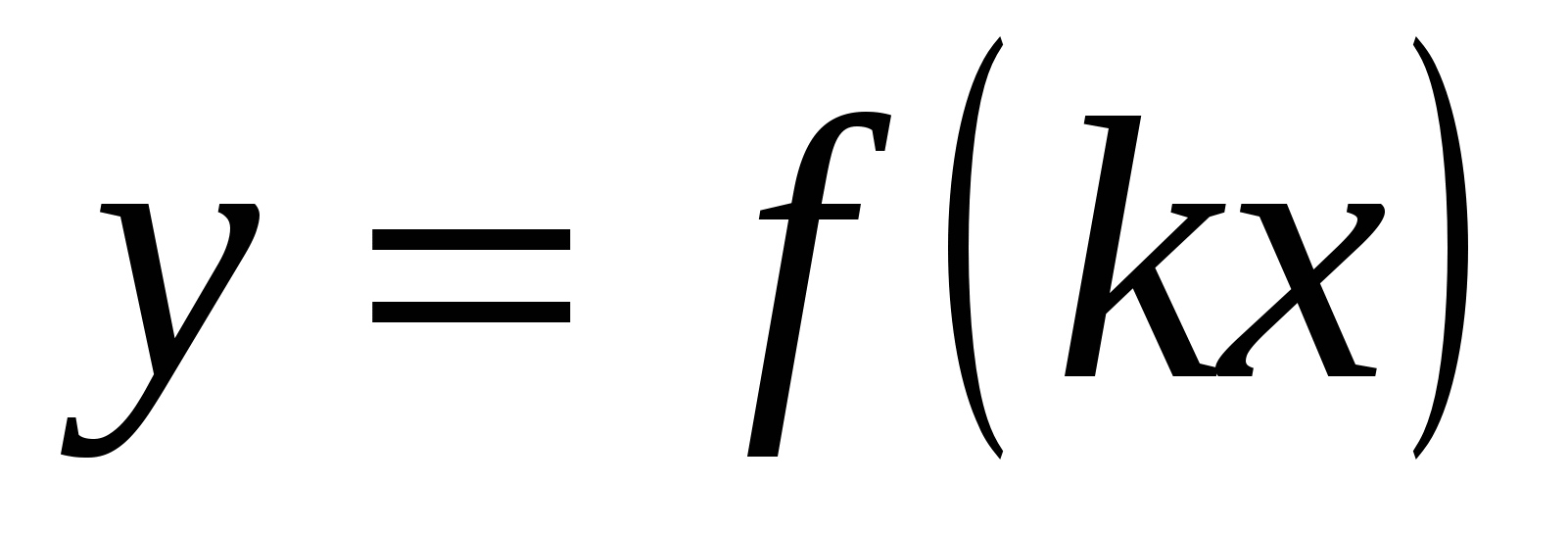 . .
|
Построение графика функции 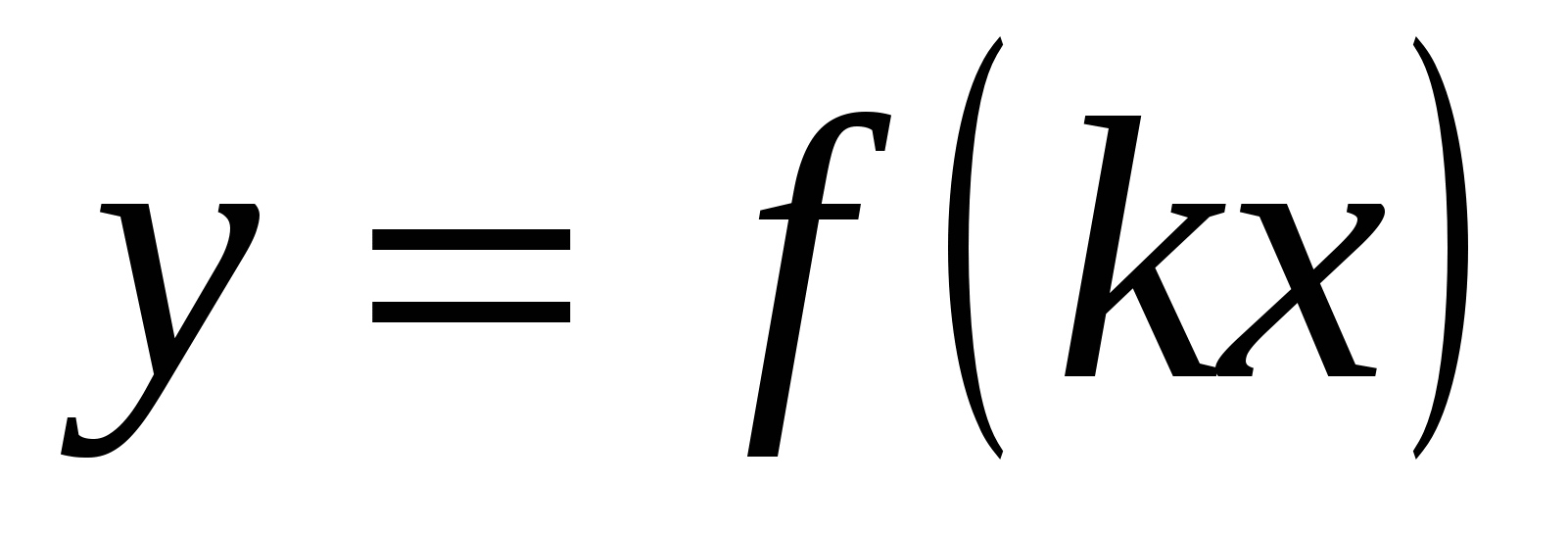 . .
|
19. График гармонического колебания.
|
График гармонического колебания.
|
20.Функции 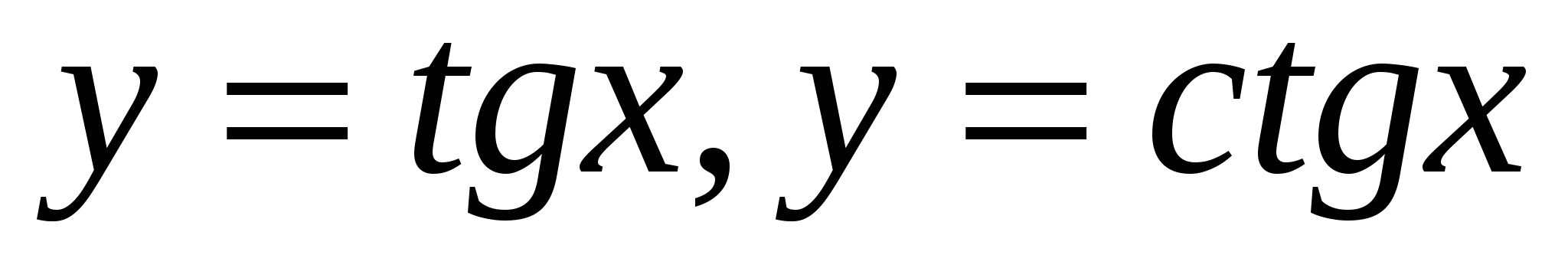 , их свойства и графики. , их свойства и графики.
|
Построение графиков функций 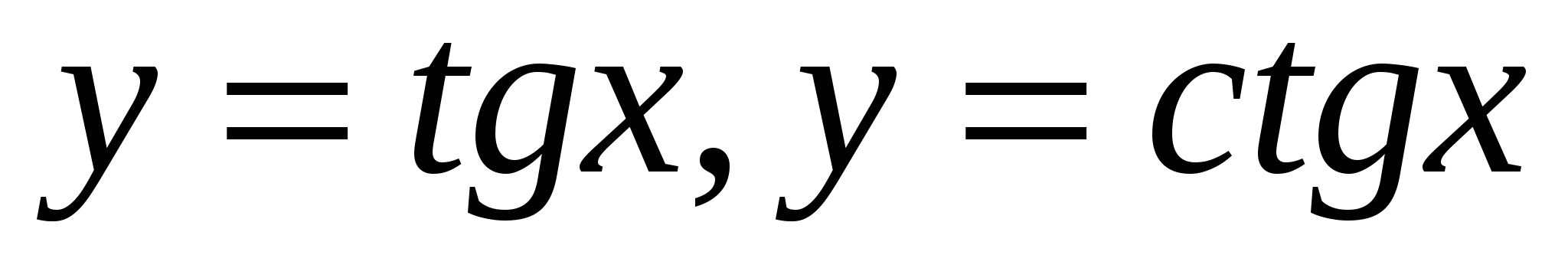 и работа с ними. и работа с ними.
|
21. Обратные тригонометрические функции.
|
Функции 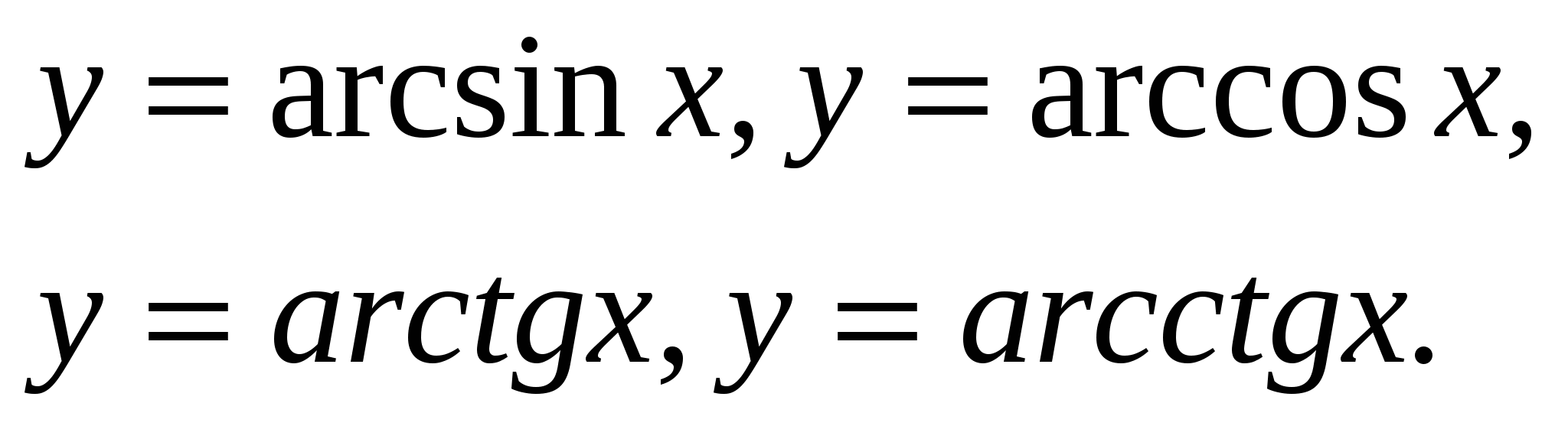
Преобразование выражений, содержащих обратные тригонометрические функции.
|
Контрольная работа № 3.
|
|
Уметь применять изученный теоретический материал при выполнении письменной работы.
|
Тригонометрические уравнения.
|
22. Простейшие тригонометрические уравнения и неравенства.
|
Решение уравнений 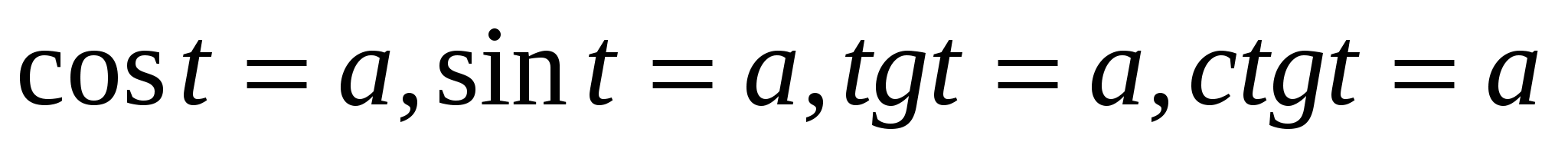
|
Знать/ понимать:
- арксинус, арккосинус, арктангенс, арккотангенс;
- формулы для решения тригонометрических уравнений;
- способы решения тригонометрических уравнений.
Уметь:
- вычислять некоторые значения обратных тригонометрические функций;
- решать простейшие тригонометрические уравнения и неравенства;
- решать однородные тригонометрические уравнения;
- показывать решения уравнений и неравенств на единичной окружности.
|
23. Методы решения тригонометрических уравнений.
|
Метод замены переменной. Метод разложения на множители. Однородные тригонометрические уравнения.
|
Контрольная работа № 4.
|
|
Уметь применять изученный теоретический материал при выполнении письменной работы.
|
Преобразование тригонометрических выражений.
|
24. Синус и косинус суммы и разности аргументов.
|
Формулы синус аи косинуса суммы и разности аргументов.
|
Знать/ понимать:
- формулы, связывающие тригонометрические функции одного и того же аргумента;
- различные способы решения тригонометрических уравнений.
Уметь:
- проводить преобразования тригонометрических выражений с использованием различных формул;
- решать тригонометрические уравнения используя различные способы.
|
25. Тангенс суммы и разности аргументов.
|
Формулы тангенса суммы и разности аргументов.
|
26. Формулы приведения.
|
Формулы приведения.
|
27. Формулы двойного аргумента. Формулы понижения степени.
|
Формулы двойного аргумента. Формулы понижения степени.
|
28. Преобразование суммы тригонометрических функций в произведение.
|
Формулы для преобразования суммы тригонометрических функций в произведение.
|
29. Преобразование произведения тригонометрических функций в сумму.
|
Формулы для преобразования произведения тригонометрических функций в сумму.
|
30. Преобразование выражения 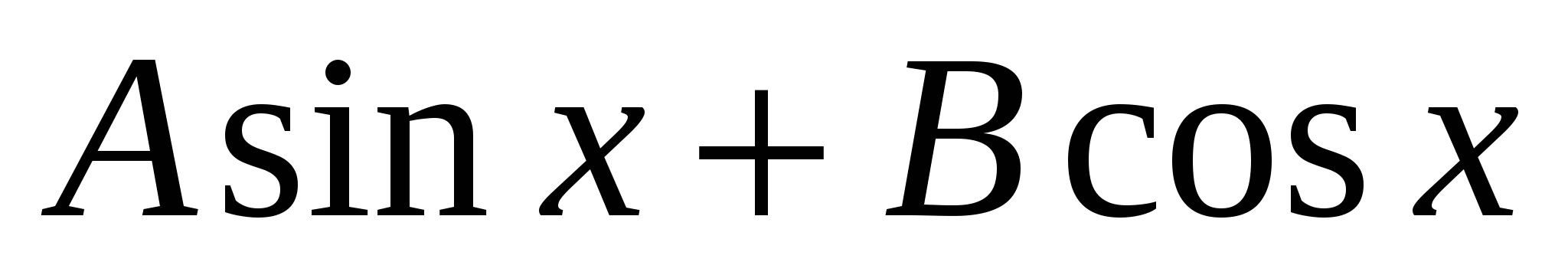 к виду к виду 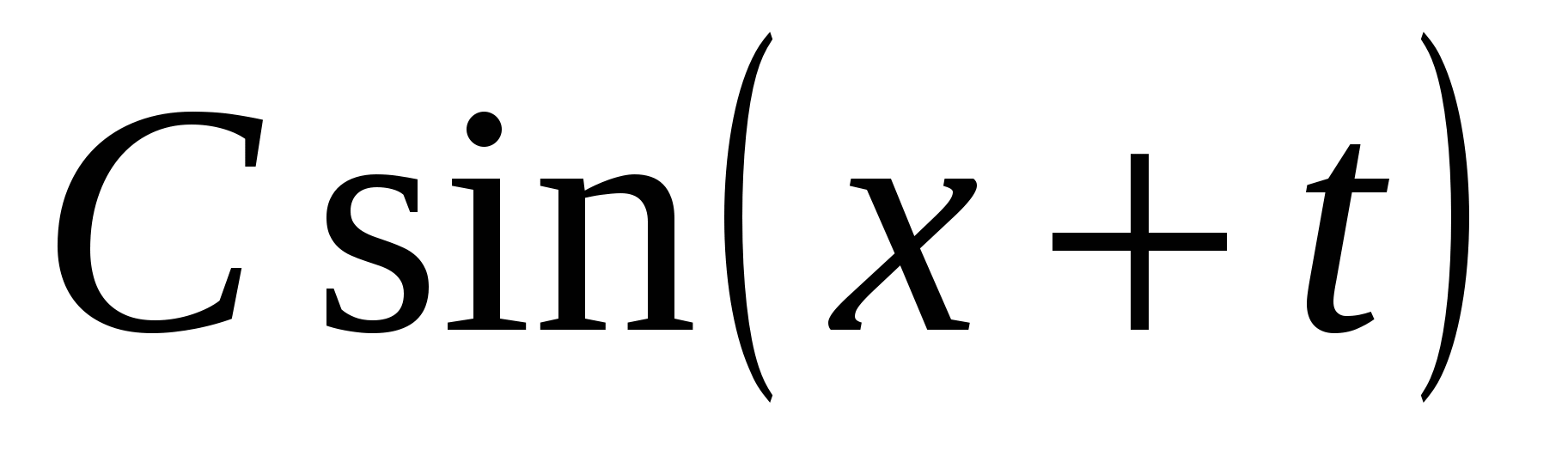 . .
|
Преобразование выражения 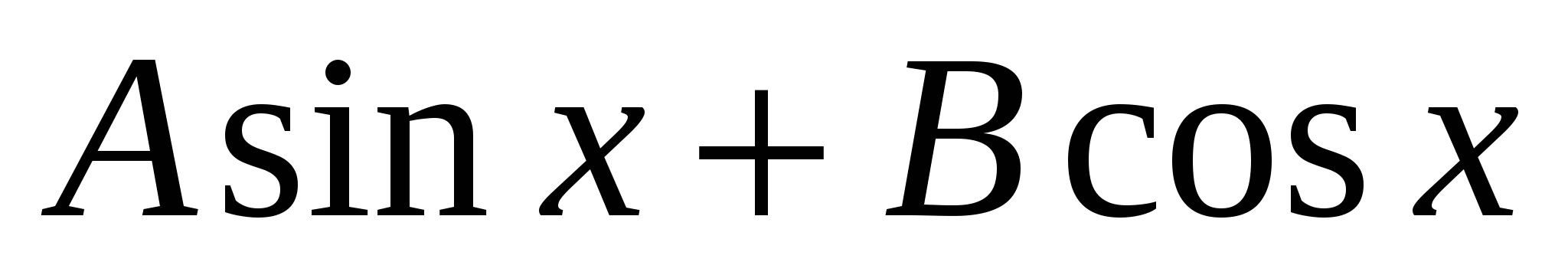 к виду к виду 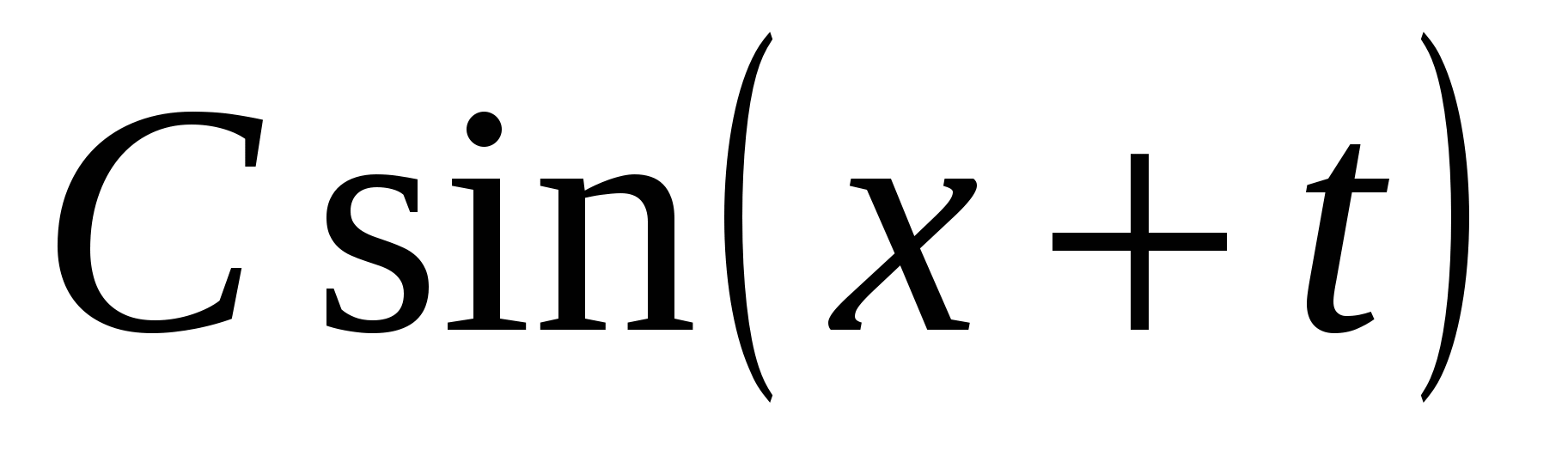 . .
|
31. Методы решения тригонометрических уравнений.
|
Универсальная тригонометрическая подстановка.
|
Контрольная работа № 5.
|
|
Уметь применять изученный теоретический материал при выполнении письменной работы.
|
Комплексные числа.
|
32. Комплексные числа и арифметические операции над ними.
|
Действительная и мнимая часть. Комплексно сопряженные числа. Модуль и аргумент комплексного числа.
|
Знать/ понимать:
- понятия комплексного числа;
- изображение комплексного числа на координатной плоскости.
Уметь:
- выполнять действия с комплексными числами;
- пользоваться геометрической интерпретацией комплексных чисел;
- в простейших случаях находить комплексные корни уравнений с действительными коэффициентами.
|
33. Комплексные числа и координатная плоскость.
|
Геометрическая интерпретация комплексных чисел.
|
34. Тригонометрическая форма записи комплексного числа.
|
Арифметические действия над комплексными числами в разных формах записи.
|
35. Комплексные числа и квадратные уравнения.
|
Решение квадратных уравнений с комплексными коэффициентами.
|
36. Возведение комплексного числа в степень. Извлечение кубического корня из комплексного числа.
|
Формулы для возведение комплексного числа в степень и извлечение кубического корня из него.
|
Контрольная работа № 6.
|
|
Уметь применять изученный теоретический материал при выполнении письменной работы.
|
Производная.
|
37. Числовые последовательности.
|
Определение числовой последовательности и способы ее задания. Свойства числовых последовательностей.
|
Знать/ понимать:
- числовая последовательность, свойства числовой последовательности;
- предел последовательности;
- формулу суммы бесконечной геометрической прогрессии;
- предел функции;
- производная, алгоритм отыскания производной;
- правила и формулы дифференцирования,
- алгоритм составления уравнения касательной к графику функции;
- алгоритм исследования функции.
Уметь:
- находить сумму бесконечно убывающей геометрической прогрессии;
- вычислять производные элементарных функций, применяя правила вычисления производных;
- решать задачи с применением уравнения касательной к графику функции;
- исследовать функции и строить их графики с помощью производной;
- решать задачи на нахождение наибольшего и наименьшего значения на отрезке.
|
38. Предел числовой последовательности.
|
Определение предела последовательности. Свойства сходящихся последовательностей. Вычисление пределов последовательностей.
|
39. Предел функции.
|
Предел функции на бесконечности. Предел функции в точке. Приращение аргумента. Приращение функции.
|
40. Определение производной.
|
Задачи, приводящие к понятию производной. Определение производной.
|
41. Вычисление производных
|
Формулы дифференцирования. Правила дифференцирования. Понятие и вычисление производных n-го порядка.
|
42. Дифференцирование сложной функции.
|
Дифференцирование обратной функции.
|
43. Уравнение касательной к графику функции.
|
Алгоритм составления уравнения касательной к графику функции.
|
44. Применение производной для исследования функций.
|
Исследование функций на монотонность. Отыскание точек экстремума. Применение производной для доказательства тождеств и неравенств.
|
45. Построение графиков функций.
|
Построение графиков функций с помощью производной.
|
46. Применение производной для отыскания наибольших и наименьших значений величин.
|
Нахождение наибольшего и наименьшего значений непрерывной функции на отрезке. Задачи на отыскание наибольшего и наименьшего значения величин.
|
Контрольные работы № 7,8.
|
|
Уметь применять изученный теоретический материал при выполнении письменной работы.
|
Комбинаторика и вероятность.
|
47. Правило умножения. Комбинаторные задачи. Перестановки и факториалы.
|
Правило умножения. Понятие факториала. Определение перестановки.
|
Знать/понимать:
- основные формулы комбинаторики;
- комбинаторные принципы сложения и умножения.
Уметь:
- решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
- вычислять коэффициенты бинома Ньютона по формуле;
- вычислять, в простейших случаях, вероятности событий на основе подсчета числа исходов.
|
48. Выбор нескольких элементов. Биноминальные коэффициенты.
|
Определение сочетаний и размещений. Формулы для нахождения числа сочетаний и размещений.
|
49. Случайные события и их вероятности.
|
Случайные события и их вероятности.
|
Введение.
|
1. Аксиомы стереометрии и некоторые следствия из аксиом.
|
Основные понятия стереометрии. Аксиомы стереометрии. Некоторые следствия из аксиом.
|
Знать/понимать:
- основные понятия стереометрии;
- основные аксиомы стереометрии.
Уметь:
- распознавать на чертежах и в моделях пространственные фигуры;
- описывать взаимное расположение точек, прямых, плоскостей с помощью аксиом стереометрии;
- применять аксиомы при решении задач.
|
Параллельность прямых и плоскостей.
|
1. Параллельность прямых, прямой и плоскости.
|
Взаимное расположение прямых в пространстве. Параллельные прямые в пространстве, свойства параллельных прямых. Параллельность прямой и плоскости, признак параллельности прямой и плоскости, их свойства.
|
Знать/понимать:
- определение параллельных и скрещивающихся прямых в пространстве;
- признаки: параллельности прямой и плоскости, параллельности плоскостей, скрещивающихся прямых;
- свойства параллельных прямых и параллельных плоскостей;
- угол между пересекающимися, параллельными и скрещивающимися прямыми;
- элементы тетраэдра и параллелепипеда;
- свойства противоположных граней и диагоналей.
Уметь:
- описывать взаимное расположение прямых, прямых и плоскостей в пространстве;
- распознавать на чертежах и в моделях параллельные, скрещивающиеся и пересекающиеся прямые;
- находить угол между прямыми в пространстве;
- выполнять чертеж по условию задачи;
- применять определения, признаки и свойства при решении простейших задач;
- строить сечения тетраэдра и параллелепипеда плоскостью.
|
2. Взаимное расположение прямых в пространстве. Угол между двумя прямыми.
|
Скрещивающиеся прямые. Угол между прямыми.
|
3. Параллельность плоскостей.
|
Параллельные плоскости, признак параллельности плоскостей. Свойства параллельных плоскостей.
|
4. Тетраэдр и параллелепипед.
|
Тетраэдр. Параллелепипед. Изображение тетраэдра и параллелепипеда на плоскости. Сечение тетраэдра и
параллелепипеда.
|
Контрольные работы по темам «Взаимное расположение прямых» и «Параллельность плоскостей».
|
|
Уметь применять изученный теоретический материал при выполнении письменной работы.
|
Перпендикулярность прямых и плоскостей.
|
1. Перпендикулярность прямой и плоскости.
|
Перпендикулярность прямых в пространстве. Параллельные прямые, перпендикулярные к плоскости. Признак перпендикулярности прямой и плоскости.
|
Знать/понимать:
- определения: перпендикулярных прямых, перпендикулярных прямой и плоскости; расстояние от точки до прямой, от прямой до плоскости, расстояние между параллельными плоскостями; угла между прямой и плоскостью;
- свойства прямых, перпендикулярных к плоскости;
- признак перпендикулярности прямой и плоскости;
- наклонная и ее проекция на плоскость;
- теорему о трех перпендикулярах;
- определение и признак перпендикулярности двух плоскостей;
- двугранный угол;
- определение прямоугольного параллелепипеда и его свойства.
Уметь:
- распознавать и описывать взаимное расположение плоскостей в пространстве, выполнять чертеж по условию задачи;
- находить наклонную и ее проекцию, определять расстояние от точки до плоскости;
- строить линейный угол двугранного угла, находить его величину;
- применять изученные признаки и свойства при решении задач.
|
2. Перпендикуляр и наклонные. Угол между прямой и плоскостью.
|
Расстояние от точки до прямой. Теорема о трех перпендикулярах. Угол между прямой и плоскостью.
|
3. Двугранный угол. Перпендикулярность плоскостей.
|
Двугранный угол. Признак перпендикулярности двух плоскостей. Прямоугольный параллелепипед.
|
Контрольная работа по теме «Перпендикулярность прямых и плоскостей».
|
|
Уметь применять изученный теоретический материал при выполнении письменной работы.
|
Многогранники.
|
1. Понятие многогранника. Призма.
|
Понятие многогранника. Геометрическое тело. Призма. Площадь боковой и полной поверхности призмы.
|
Знать/понимать:
- представление о многогранниках, призме и пирамиде, правильных многогранниках;
- элементы многогранника: вершины, ребра, грани;
- определения правильных призмы и пирамиды;
- виды симметрии в пространстве;
- формулы площадей боковой и полной поверхностей призмы и пирамиды.
Уметь:
- изображать призму и пирамиду, выполнять чертежи по условию задачи;
- находить площади боковой и полной поверхностей призмы и пирамиды;
- решать задачи на нахождение апофемы, бокового ребра, площади основания пирамиды.
|
2. Пирамида.
|
Пирамида. Правильная пирамида. Усеченная пирамида.
|
3. Правильные многогранники.
|
Симметрия в пространстве. Понятие правильного многогранника. Элементы симметрии правильного многогранника.
|
Контрольная работа по теме «Многогранники»
|
|
Уметь применять изученный теоретический материал при выполнении письменной работы.
|
Векторы в пространстве.
|
1. Понятие вектора в пространстве.
|
Понятие вектора. Модуль вектора. Равенство векторов. Коллинеарные векторы.
|
Знать/понимать:
- определение вектора в пространстве, его длины;
- правила сложения и вычитания векторов, умножения вектора на число, правило параллелепипеда;
- определение компланарных векторов;
- теорему о разложении вектора по трем некомпланарным векторам.
Уметь:
- на модели параллелепипеда находить сонаправленные, противоположно направленные, равные и компланарные векторы;
- находить сумму и разность векторов, выражать один из коллинеарных векторов через другой;
- выполнять разложение вектора по трем некомпланарным векторам.
|
2. Сложение и вычитание векторов. Умножение вектора на число.
|
Сложение и вычитание векторов. Сумма нескольких векторов. Умножение вектора на число.
|
3. Компланарные вектора.
|
Компланарные векторы. Правило параллелепипеда. Разложение вектора по трем некомпланарным векторам.
|
Повторение.
|
Алгебра и начала анализ.
|
Преобразование тригонометрических выражений. Решение тригонометрических уравнений и неравенств. Вычисление производных. Решение задач на применение производной.
|
Уметь использовать приобретенные знания и умения в практической деятельности для решения задач разного уровня сложности на основе изученного материала.
|
Геометрия.
|
Призма. Пирамида. Решение задач на многогранники.
|
Уметь использовать приобретенные знания и умения в практической деятельности для решения задач на основе изученных формул и свойств фигур.
|
 Скачать 0.65 Mb.
Скачать 0.65 Mb.