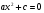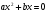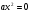Решение неполных квадратных уравнений
 Скачать 22.86 Kb. Скачать 22.86 Kb.
|
| Урок алгебры в 8 классе. тема: “Решение неполных квадратных уравнений” Цели: обучающая:
воспитывающие:
Тип урока: закрепление изученного материала. Ход урока:
2х 2 = х 4 х 2= - 25 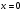 х 2= х 2=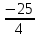 нет решения 3. х2 – 9 = 0 4. 5х2 =0 х = 3 х =5 5.36х2 +1 =0 6. 3х2 – 9 = 0 36х2 = 1 х2 – 3 = 0 х 2= 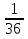 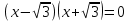 х = 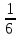 ; х = ; х =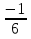 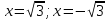 . .3. Систематизация знаний. После решения уравнений, нахождения ошибок и повторения алгоритмов решения, учащиеся парами составляют таблицу:
В тетрадях совместно заполняют таблицу. Проверяем, обсуждаем.
4. После этого выполним трехуровневую самостоятельную работу. Уровень учащиеся выбирают сами. Самостоятельная работа: I уровень (обязательный) 8х2 =0; х 2 + 7х = 0; 2х2 - 18 = 0. II уровень (средний) 9 х 2 - 16 = 0; 2х2 = 3х; 2 = 7х2 +2. III уровень (повышенный) - 0,3х2 + 9 = 0 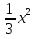 + + 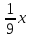 =0 =0При каком a один из корней уравнения равен 1? 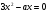 На скрытой части доски после решения самостоятельной работы учитель представляет ответы и частичное решение уравнений, учащиеся могут оценить результат своей работы. 5. В качестве домашнего задания учитель предлагает разноуровневые задания. 1. Уровень: а) 3 х 2 - 9 = 0; б) х 2 - 2х = 0; в) х2 + 9 = 0; г) 2х2+8 = 0. 2. Уровень: a) 25 х 2 - 49 = 0; б) 3х 2 - 5х = 0; в) 3х2 + 27 = 0; г) 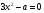 . При каком a один из корней уравнения равен 1? . При каком a один из корней уравнения равен 1?3. Уровень: a) 5 – 0,2х 2 = 0; б) 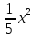 - - 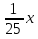 =0 =0в) (3х + 2)2 = 4+12х; г) х2 +(а +1)(х + а – 8) =0. При каком значении a корни уравнения являются противоположными числами? 6. Итог урока: если хватает времени, то можно самостоятельно проверить свои работы, сверив ответы с доской (на оборотной стороне), выставление отметок, запись домашнего задания. |