№ пункта
|
№ урока
|
Дата
|
Название изучаемой темы
|
Круг изучаемых вопросов
|
Домашнее задание
|
Кол-во часов
|
|
|
|
Глава I.
|
Функции. Производные. Интегралы
|
|
51 час
|
|
|
|
§ 1. Функции и их графики.
|
|
|
9 часов
|
П.1.1
|
Урок 1
|
|
Элементарные функции.
|
Понятия аргумента, функции, области определения функции, сложной функции, суперпозиции двух функций, элементарной функции.
|
Глава I.
§1.п.1.1, № 1.1, 1.2, 1.3, 1.4 (устно), №65(а), 78(е), 92(з)
|
1 час
|
П.1.2
|
Урок 2
|
|
Область определения и область изменения функции. Ограниченность функции.
|
Понятие области изменения (значения) функции, области существования функции. Функция, ограниченная снизу; функция, ограниченная сверху. Наибольшее и наименьшее значение функции.
|
§1.п.1.2, № 1.6, 1.7 (устно), №1.10 (ж,з), 1.14(в)
|
1 час
|
П.1.3
|
Урок 3
|
|
Четность. Нечетность, периодичность функций.
|
Понятие четной, нечетной функции. Периодическая функция, период функции, главный период функции. Примеры.
|
§1.п.1.3, № 1.15, 1.28 (устно), №1.18(б), 1.19(д), 1.32 (в,е)
|
2 часа
|
Урок 4
|
|
§1.п.1.3 ,№1.20(б),1.31
|
П.1.4.
|
Урок 5
|
|
Промежутки возрастания, убывания, знакопостоянства и нули функции
|
Понятие возрастающей, убывающей функции, невозрастающей, неубывающей функции, строго монотонной функции. Монотонная функция. Нуль функции. Промежутки знакопостоянства.
|
§1.п.1.4, № 1.37,1.38(устно), № 1.47(б,д)
|
2 часа
|
Урок 6
|
|
§1.п.1.4, № 1.49(г),1.50 (б)
|
П.1.5.
|
Урок 7
|
|
Исследование функций и построение их графиков элементарными методами.
|
Алгоритм исследования функции. Функция, непрерывная на данном промежутке.
|
§1.п.1.5, № 1.52, 1.53 (устно), №1.55(а), 1.56(а), 1.57(а)
|
1 час
|
П.1.6
|
Урок 8
|
|
Основные способы преобразования графиков.
|
Симметрия относительно осей координат. Сдвиг вдоль осей координат (параллельный перенос). Растяжение и сжатие графика вдоль осей координат. Построение графика функции у=Аf(k(x-a))+В по графику функции у=f(x). Симметрия относительно у=х.
|
§1.п.1.6, № 1.59, 1.63, 1.71
|
1 час
|
П.1.7.
|
Урок 9
|
|
Графики функций, содержащих модули
|
Построение графиков функций, связанных с модулем.
|
§1.п.1.7, № 1.81(б), 1.82(д), 1.83(б)
|
1 час
|
|
|
|
§2. Предел функции и непрерывность.
|
|
|
5 часов
|
П.2.1
|
Урок 10
|
|
Понятие предела функции.
|
Понятие предела функции. Примеры.
|
§2.п.2.1, № 2.4(в), 2.5(б)
|
1 час
|
П.2.2
|
Урок 11
|
|
Односторонние пределы.
|
Понятие правой окрестности точки, правого предела в точке. Понятие левой окрестности точки, левого предела в точке. Предел функции в точке.
|
§2.п.2.2, №2.8, 2.12.
|
1 час
|
П.2.3
|
Урок 12
|
|
Свойства пределов функций.
|
Свойства пределов функций. Примеры.
|
§2.п.2.3, №2.15(д,з), 2.17(а,г), 2.19(а,г)
|
1 час
|
П.2.4
|
Урок 13
|
|
Понятие непрерывности функции.
|
Приращение аргумента, приращение функции. Разрывной график. Функция, непрерывная в точке. Функция непрерывная справа и слева в точке, функция непрерывная на отрезке.
|
§2.п.2.4, №2.23, 2.28, 2.32(г)
|
1 час
|
П.2.5.
|
Урок 14
|
|
Непрерывность элементарных функций.
|
Теорема о непрерывности элементарных функций.
|
§2.п.2.5, №2.34, 2.36(б)
|
1 час
|
|
|
|
§ 3. Обратные функции.
|
|
|
6 часов
|
П.3.1.
|
Урок 15
|
|
Понятие обратной функции.
|
Понятие обратной функции. Примеры.
|
§3.п.3.1, № 3.1(в,е), 3.5(г)
|
1 час
|
П.3.2.
|
Урок 16
|
|
Взаимно обратные функции.
|
Понятие взаимно-обратной функции. Свойство графиков взаимно-обратных функций.
|
§3.п.3.2, № 3.8(б,е), 3.9(д), 3.14
|
1 час
|
П.3.3.
|
Урок 17
|
|
Обратные тригонометрические функции.
|
Функция у=arcsinx. Функция у=arccosx. Функция у=arctgx. Функция у=arcctgx. Свойства обратных тригонометрических функций. Основные обратные тригонометрические функции.
|
§3.п.3.16(б), 3.17(д)
|
2 часа
|
Урок 18
|
|
§3.п.3.17(в,е)
|
П.3.4
|
Урок 19
|
|
Примеры использования обратных тригонометрических функций. Подготовка к контрольной работе.
|
Примеры использования обратных тригонометрических функций.
|
§3.п.3.20(и,к), 3.21(з,о)
|
1 час
|
|
Урок 20
|
|
Контрольная работа № 1 по теме:
|
«Функции и их графики. Предел функции и непрерывность»
|
№228, 82
|
1 час
|
|
|
|
§ 4. Производная
|
|
|
11 часов
|
П.4.1.
|
Урок 21
|
|
Анализ контрольной работы. Понятие производной.
|
Мгновенная скорость. Приращение времени. Приращение пути. Приращение аргумента. Приращение функции. Дифференцирование функции. Производная функции. Правая и левая производные функции. Механический смысл производной. Угол наклона касательной. Геометрический смысл производной.
|
§4. п.4.1, №4.7, 4.3
|
2 часа
|
Урок 22
|
|
§4. п.4.1, №4.13, 4.11
|
П.4.2.
|
Урок 23
|
|
Производная суммы. Производная разности.
|
Теоремы о производной суммы и о производной разности. Следствие из теорем. Формулы.
|
§4. п.4.2,
№4.18 (3 ст.),2.19(б,г,е,з)
|
2 часа
|
Урок 24
|
|
§4. п.4.2 №4.21(в), 4.22(б,г)
|
П.4.3.
|
Урок 25
|
|
Непрерывность функций, имеющих производную. Дифференциал.
|
Теорема о функции непрерывной в точке. Дифференциал функции. Дифференциал функции.
|
§4. п.4.25(2), 4.27(б,г)
|
1 час
|
П.4.4.
|
Урок 26
|
|
Производная произведения. Производная частного.
|
Теоремы о производной произведения и производной частного. Формулы. Примеры.
|
§4. п.4.4, № 4.30 (2 ст.), 4.31
|
2 часа
|
Урок 27
|
|
§4. п.4.4, № 4.33 (2 ст.), 4.34
|
П.4.5.
|
Урок 28
|
|
Производные элементарных функций.
|
Шесть теорем о производных элементарных функций. Формулы. Примеры.
|
§4. п.4.5, № 4.39 (б,г), 4.31, 4.43(г), 4.44 (б), 4.45(в), 4.48(е), 4.50.
|
1 час
|
П.4.6.
|
Урок 29
|
|
Производная сложной функции. Подготовка к контрольной работе.
|
Теоремы о производной сложной функции. Примеры.
|
§4. п.4.6, № 4.52(в,е,и), 4.54(б,г), 4.55(г), 4.60
|
2 часа
|
Урок 30
|
|
§4. п.4.6, № 4.63, 4.64(е,з),4.65(б)
|
|
Урок 31
|
|
Контрольная работа № 2 по теме:
|
«Производная»
|
№185,179
|
1 час
|
|
|
|
§ 5. Применение производной.
|
|
|
16 часов
|
П.5.1
|
Урок 32
|
|
Анализ контрольной работы. Максимум и минимум функции.
|
Понятие максимума и минимума функции на отрезке. Точки максимума и минимума. Точки локального максимума и минимума. Точки локального экстремума. Равенство производной нулю в точке локального экстремума. Критические точки.
|
§5. п.5.1, № 5.7,5.10(б,г)
|
2 часа
|
Урок 33
|
|
§5. п.5.1, № 5.12,5.16
|
П.5.2.
|
Урок 34
|
|
Уравнение касательной.
|
Теорема об уравнении касательной. Примеры.
|
§5. п.5.2, № 5.21,5.24
|
2 часа
|
Урок 35
|
|
§5. п.5.2, № 5.29,5.31
|
П.5.3.
|
Урок 36
|
|
Приближенные вычисления.
|
Нахождение приближенных значений функций. Примеры.
|
§5. п.5.3, № 5.38(в,г), 5.41(г,ж,з).
|
1 час
|
П.5.5.
|
Урок 37
|
|
Возрастание и убывание функций
|
Понятия возрастания и убывания функций на промежутке. Теорема о возрастании и убывании функции на промежутке. Определение точек локального максимума и минимума при изменении знака производной.
|
§5. п.5.5, № 5.50(е,з), 5.51(б,д),5.53
|
2 часа
|
Урок 38
|
|
§5. п.5.5, № 5.57, 5.58(б)
|
П.5.6
|
Урок 39
|
|
Производные высших порядков.
|
Вторая производная функции. Производные высших порядков. Механический смысл второй производной.
|
§5. п.5.6, № 5.66,5.68
|
1 час
|
П.5.8.
|
Урок 40
|
|
Экстремум функции с единственной критической точкой.
|
Три утверждения о экстремуме функции с единственной критической точкой.
|
§5. п.5.8, № 5.83(б,г),5.83(г)
|
2 часа
|
Урок 41
|
|
§5. п.5.8, № 5.84(а),5.88
|
П.5.9.
|
Урок 42
|
|
Задачи на максимум и минимум.
|
Разбор примеров задач на максимум и минимум.
|
§5. п.5.9, № 5.93, 5.95
|
2 часа
|
Урок 43
|
|
§5. п.5.9, № 5.98,5.101
|
П.5.10.
|
Урок 44
|
|
Асимптоты. Дробно-линейная функция.
|
Асимптоты к прямой. Асимптоты кривой. Наклонные, горизонтальные вертикальные асимптоты. Дробно-линейные функции.
|
§5. п.5.10, № 5.107, №5.109(а)
|
1 час
|
П.5.11.
|
Урок 45
|
|
Построение графиков функций с помощью производной. Подготовка к контрольной работе.
|
Построение различных графиков функций.
|
§5. п.5.11, № 5.114(б,д),5.115(г)
|
2 часа
|
Урок 46
|
|
§5. п.5.11, № 5.117(д), 5.121(б,г)
|
|
Урок 47
|
|
Контрольная работа № 3 по теме:
|
«Применение производной»
|
№210,226
|
1 час
|
|
|
|
§ 6. Первообразная и интеграл.
|
|
|
13 часов
|
П.6.1
|
Урок 48
|
|
Анализ контрольной работы. Понятие первообразной.
|
Понятие первообразной. Формула для первообразной. Неопределенный интеграл. Основное свойство неопределенного интеграла.
|
§6. п.6.1, № 6.2(д,к,м), 6.6(в),6.7(г)
|
3 часа
|
Урок 49
|
|
§6. п.6.1, № 6.9(б,д), 6.13(2ст.),6.14(г)
|
Урок 50
|
|
§6. п.6.1, № 6.15(б), 6.17(2ст.)
|
П.6.3
|
Урок 51
|
|
Площадь криволинейной трапеции.
|
Криволинейная трапеция. Площадь криволинейной трапеции. Интегральная сумма.
|
§6. п.6.3, № 6.27
|
1 час
|
П.6.4
|
Урок 52
|
|
Определенный интеграл.
|
Интегрирование функции. Определенный интеграл. Геометрический смысл определенного интеграла.
|
§6. п.6.4, № 6.33,6.35(а)
|
2 часа
|
Урок 53
|
|
§6. п.6.4, № 6.34(в), 6.36(б)
|
П.6.5
|
Урок 54
|
|
Приближенное вычисление определенного интеграла.
|
Нижняя и верхняя интегральная сумма. Метод трапеции.
|
§6. п.6.5, № 6.41(б), 6.43(б)
|
1 час
|
П.6.6
|
Урок 55
|
|
Формула Ньютона-Лейбница.
|
Теорема Ньютона-Лейбница. Производная интеграла.
|
§6. п.6.6, № 6.46(в),6.47(в),6.48(в),6.49(в), 6.50(в),6.51(в)
|
3 часа
|
Урок 56
|
|
§6. п.6.6, № 6.53(в),6.54(в),6.55(в),6.56(в)
|
Урок 57
|
|
§6. п.6.6, № 6.57(в),6.60
|
П.6.7.
|
Урок 58
|
|
Свойства определенных интегралов.
|
Свойства определенного интеграла. Примеры.
|
§6. п.6.7, № 6.64(г), 6.66(б,г) 6.68(б), 6.73(в,е)
|
1 час
|
П.6.8.
|
Урок 59
|
|
Применение определенных интегралов в геометрических и физических задачах. Подготовка к контрольной работе.
|
Площадь круга. Объем тела вращения. Масса стержня переменной плоскости. Работа электрического заряда. Давление жидкости на стенку. Центр тяжести.
|
§6. п.6.8, № 6.79
|
1 час
|
|
Урок 60
|
|
Контрольная работа № 4 по теме:
|
«Первообразная и интеграл»
|
№ 9, 54, 95
|
1 час
|
|
|
|
§7. Равносильность уравнений и неравенств
|
|
|
4 часа
|
|
Урок 61
|
|
Равносильные преобразования уравнений
|
|
|
2 часа
|
Урок 62
|
|
|
Урок 63
|
|
Равносильные преобразования неравенств
|
|
|
2 часа
|
Урок 64
|
|
|
|
|
|
|
|
|
|
|
|
§ 8. Уравнения следствия.
|
|
|
8 часов
|
П.8.1
|
Урок 65
|
|
Анализ контрольной работы. Понятие уравнения-следствия.
|
Уравнение-следствие. Переход к уравнению-следствию. Корни, посторонние для данного уравнения. Проверка полученных корней. Возведение уравнения в натуральную степень п. Потенцирование уравнения. Освобождение уравнения от знаменателя. Приведение подобных членов. Применение некоторых формул, приводящих к уравнению-следствию. Потеря корней уравнения.
|
§7. п.7.1., № 7.3(в), 7.4(д), 7.5(г,е),7.6(з,л)
|
1 час
|
П.8.2
|
Урок 66
|
|
Возведение уравнения в четную степень
|
Иррациональные уравнения. Возведение уравнения в четную степень.
|
§7. п.7.2., № 7.10(б), 7.11(в), 7.12(б), 7.13(а), 7.14(г)
|
2 часа
|
Урок 67
|
|
§7. п.7.2., № 7.16(а), 7.17(а), 7.18(а), 7.19(б)
|
П.8.3
|
Урок 68
|
|
Потенцирование уравнений.
|
Алгоритм потенцирования логарифмических уравнений.
|
§7. п.7.3., № 7.22(г), 7.23(б), 7.24(б),
|
2 часа
|
Урок 69
|
|
§7. п.7.3., 7.25(а), 7.26(а)
|
П.8.4
|
Урок 70
|
|
Другие преобразования, приводящие к уравнению-следствию.
|
Освобождения уравнений от знаменателя. Приведение подобных членов уравнения. Применение некоторых формул.
|
§7. п.7.4., № 7.29(г,е), 7.30(в,д), 7.33(е,з), 7.38
|
1 час
|
П.8.5
|
Урок 71
|
|
Применение нескольких преобразований, приводящих к уравнению-следствию.
|
Преобразования, приводящие к уравнению-следствию. Примеры.
|
§7. п.7.5., № 7.71(в), 7.42(в), 7.44(г
|
2 часа
|
Урок 72
|
|
§7. п.7.5., 7.47(а), 7.48(а)
|
|
|
|
§ 9. Равносильность уравнений и неравенств системам.
|
|
|
13 часов
|
П.9.1
|
Урок 73
|
|
Анализ контрольной работы. Основные понятия.
|
Система уравнений. Понятие решения системы. Равносильность двух систем. Равносильность уравнения (неравенства) системе. Равносильность уравнения (неравенства) совокупности нескольких систем.
|
§11. п.11.1., № 11.3, 11.6(б)
|
1 час
|
П. 9.2 - 9.3
|
Урок 74
|
|
Решение уравнений с помощью систем.
|
Алгоритм решения уравнений с помощью систем.
|
§11. п.11.3., № 11.16(г), 11.17(в), 11.19(б),
|
4 часа
|
Урок 75
|
|
§11. п.11.3., 11.20(а), 11.21(г), 11.22(в)
|
Урок 76
|
|
§11. п.11.3., № 11.23(в), 11.24(а),
|
Урок 77
|
|
§11. п.11.3., 11.25(б), 11.26(б), 11.30(а)
|
П.9.4
|
Урок 78
|
|
Уравнения вида f(α(x))=f(β(x)).
|
Теорема о равносильности уравнения f(α(x))=f(β(x)) системе 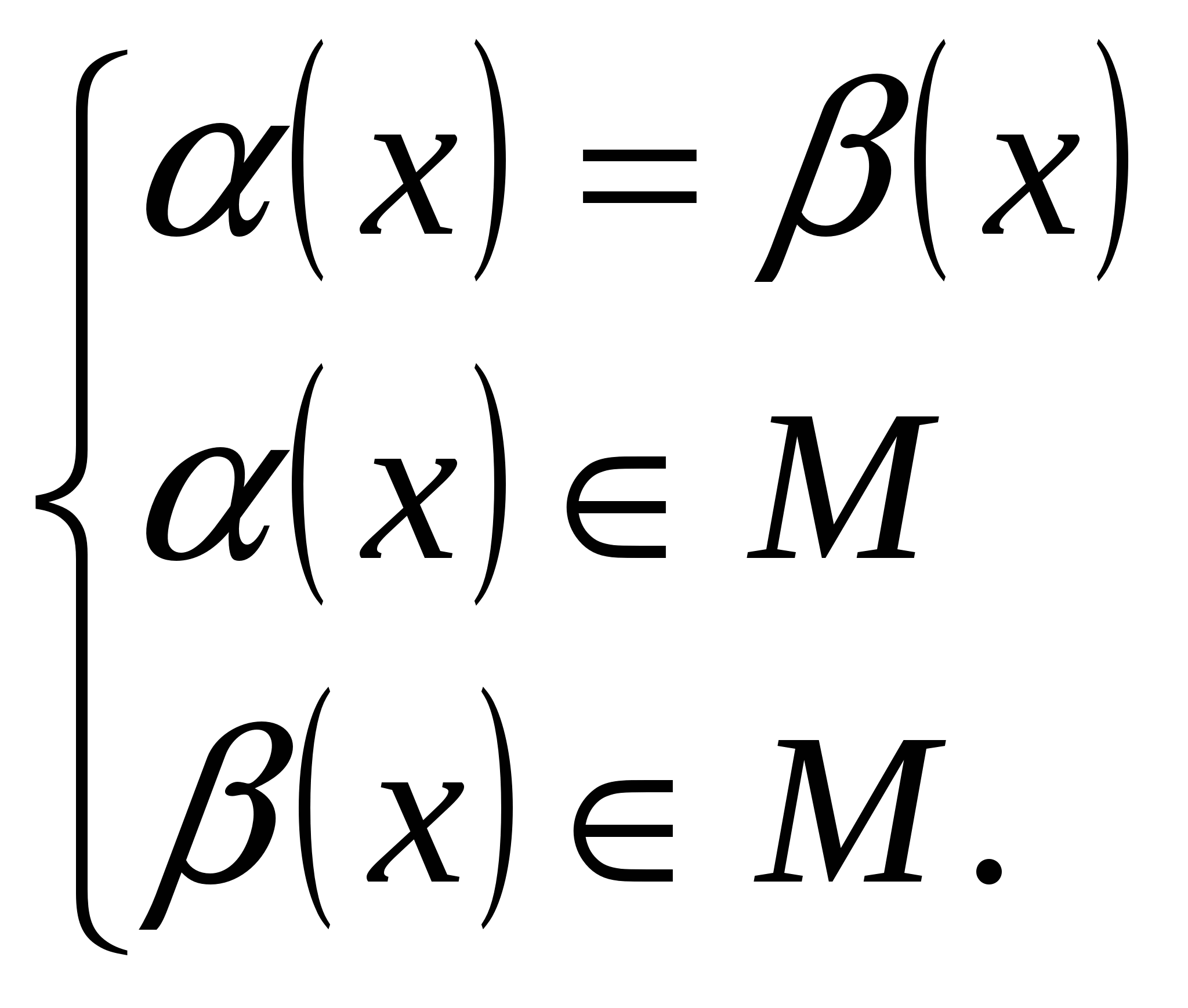 . .
|
§11. п.11.4., № 11.36(в), 11.37(б), 11.40(а)
|
2 часа
|
Урок 79
|
|
§11. п.11.4., № 11.41(б), 11.42(а), 11.43(а), 11.46(а)
|
П.9.5 – 9.6
|
Урок 80
|
|
Решение неравенств с помощью систем.
|
Алгоритм решения неравенств с помощью систем.
|
§11. п.11.5., № 11.51(б), 11.54(а), 11.55(а), 11.56(в), 11.58
|
4 часа
|
Урок 81
|
|
§11. п.11.5., № 11.52(б), 1.57(а), 1.58(а)
|
Урок 82
|
|
§11. п.11.5., № 11.61(г), 11.63(а), 11.66(а)
|
Урок 83
|
|
§11. п.11.5., № 11.59(б), 11.64(а)
|
П.9.7
|
Урок 84
|
|
Неравенства вида f(α(x))>f(β(x)).
|
Теорема о равносильности неравенства f(α(x))>f(β(x)) системам 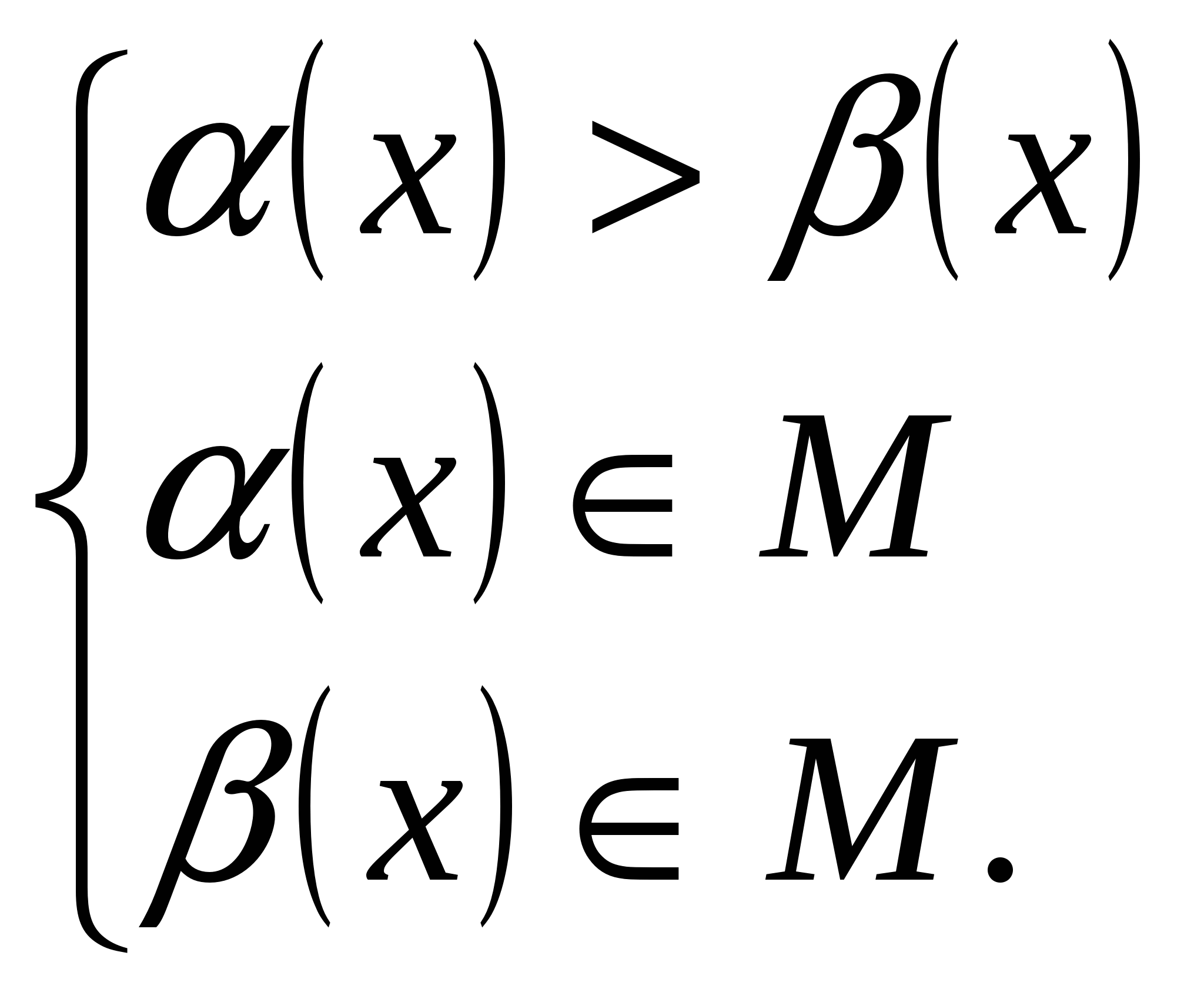 и и 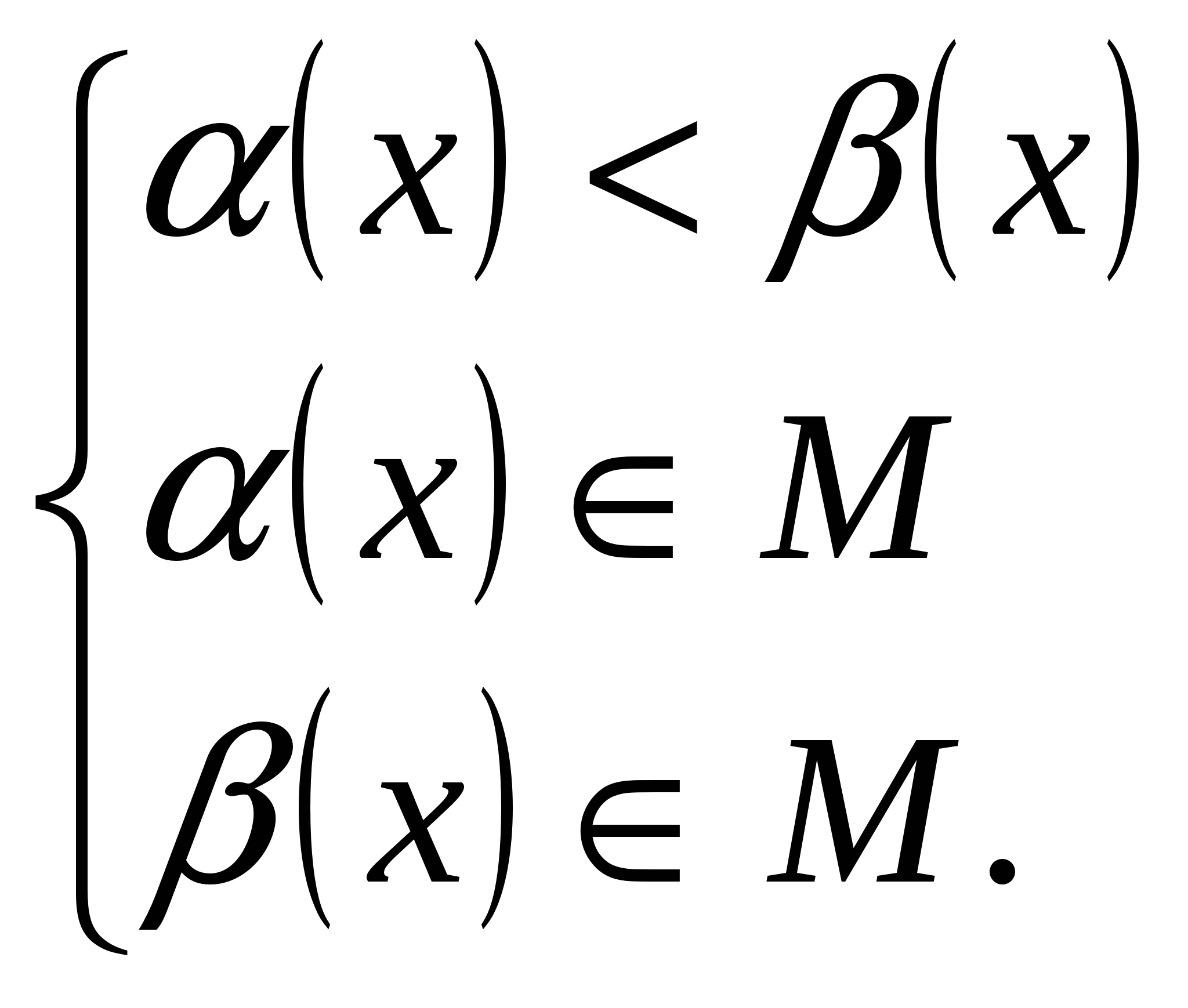 . Частный случай теоремы. . Частный случай теоремы.
|
§11. п.11.6., № 11.72(в), 11.73(в)
|
2 часа
|
Урок 85
|
|
§11. п.11.6., № 11.78(а), 11.80(а), 11.81(б), 11.83(а)
|
|
|
|
|
|
|
|
|
|
|
§ 10. Равносильность уравнений на множествах.
|
|
|
7 часов
|
П.10.1
|
Урок 86
|
|
Основные понятия.
|
Уравнения, равносильные на множестве. Преобразования, приводящие данное уравнение к уравнению, равносильному ему на множестве.
|
§8. п.8.1., № 8.4(г,е,з), 8.5(ж,и,л)
|
1 час
|
П.10.2
|
Урок 87
|
|
Возведение уравнения в четную степень.
|
Утверждения, используемые при возведении уравнения в четную степень.
|
§8. п.8.2., № 8.8(б), 8.9(в),8.10(г), 8.11(а)
|
2 часа
|
Урок 88
|
|
§8. п.8.2., № 8.14(б,г),8.16
|
П.10.3
|
Урок 89
|
|
Умножение уравнения на функцию.
|
Алгоритм умножения уравнения на функцию. Примеры.
|
§8. п.8.4., № 8.28(в), 8.29(г), 8.30(б), 8.31(г), 8.33(а), 8.34(в)
|
1 час
|
П.10.4
|
Урок 90
|
|
Другие преобразования уравнений. Подготовка к контрольной работе.
|
Приведение подобных членов. Применение некоторых формул. Алгоритмы решения уравнений.
|
§8. п.8.5., № 8.37(в), 8.38(в), 8.40(а), 8.41(б)
|
1 час
|
П.10.5
|
Урок 91
|
|
Применение нескольких преобразований.
|
-
|
№ 55, 65(в), 62-
|
1 час
|
|
Урок 92
|
|
Контрольная работа № 5 по теме:
|
«Уравнения-следствия. Равносильность уравнений на множествах».
|
|
1 час
|
|
|
|
§ 11. Равносильность неравенств на множествах.
|
|
|
6 часов
|
П.11.1
|
Урок 93
|
|
Анализ контрольной работы. Основные понятия.
|
Неравенства, равносильные на множестве. Равносильный переход на множестве. Основные преобразования неравенств, приводящих данное неравенство к неравенству, равносильному ему.
|
§9. п.9.1., № 9.
|
1 час
|
П.11.2
|
Урок 94
|
|
Возведение неравенств в четную степень.
|
Доказательство утверждений, используемых при возведении неравенства в натуральную степень. Алгоритм возведения неравенства в натуральную степень.
|
§9. п.9.2., № 9.8(б,г, ), 9.9(г), 9.10(б), 9.11(а), 9.12(б), 9.13(б)
|
1час
|
П.11.3
|
Урок 95
|
|
Умножение неравенства на функцию.
|
Утверждения, используемые при умножении неравенства на функцию. Алгоритм умножения неравенства на функцию.
|
§9. п.9.4., № 9.9.33(б), 9.35(а), 9.36(в,г)
|
1 час
|
П.11.4
|
Урок 96
|
|
Другие преобразования неравенств.
|
Приведение подобных членов неравенства. Применение некоторых формул. Алгоритмы некоторых других преобразований неравенства.
|
§9. п.9.5., № 9.38(б,г), 9.39(в), 9.41(а), 9.42(а)
|
1 час
|
П.11.5
|
Урок 97
|
|
Применение нескольких преобразований.
|
-
|
-
|
1 час
|
П.11.7.
|
Урок 98
|
|
Нестрогие неравенства.
|
Правила решения нестрогих неравенств. Алгоритм решения нестрогих неравенств.
|
§9. п.9.8., № 9.61(б), 9.63(г), 9.64(а), 9.65(в), 9.66(г), 9.67(в)
|
1 час
|
|
|
|
§ 12. Метод промежутков для уравнений и неравенств.
|
|
|
4 часа
|
П.12.1
|
Урок 99
|
|
Уравнения с модулями.
|
Метод промежутков. Алгоритм решения уравнения с модулями.
|
§10. п.10.1., № 10.2(в), 10.3(а), 10.4(г), 10.5(б), 10.7(г,е)
|
1 час
|
П.12.2
|
Урок 100
|
|
Неравенства с модулями.
|
Метод промежутков. Алгоритм решения неравенств с модулями.
|
§10. п.10.2., № 10.10(в,г), 10.11(б), 10.14(а), 10.15(б)
|
1 час
|
П.12.3
|
Урок 101
|
|
Метод интервалов для непрерывных функций. Подготовка к контрольной работе.
|
Метод интервалов для непрерывных функций.
|
§10. п.10.3., № 10.19(а,в), 10.22(б), 10.23(б)
|
1 час
|
|
Урок102
|
|
Контрольная работа № 6 по теме:
|
«Равносильность неравенств на множествах. Метод промежутков для уравнений и неравенств».
|
№ 58, 86, 223
|
1 час
|
|
|
|
§ 13. Использование свойств функций при решении уравнений и неравенств.
|
|
|
5 часов
|
П.13.1
|
Урок103
|
|
Использование областей существования функций
|
Примеры использования областей функций.
|
§12. п.12.1., № 12.1(б), 12.3(в), 12.4(в).
|
1 час
|
П.13.2
|
Урок104
|
|
Использование неотрицательности функций.
|
Примеры использования неотрицательности функций.
|
§12. п.12.2., № 12.7(б), 12.9(в), 12.11(в)
|
1 час
|
П.13.3
|
Урок105
|
|
Использование ограниченности функций.
|
Примеры использования ограниченности функций.
|
§12. п.12.3., № 12.15(а), 2.17(б), 12.21(б)
|
1 час
|
П.13.4
|
Урок106
|
|
Использование монотонности и экстремумов функций
|
|
|
1 час
|
П.13.5
|
Урок107
|
|
Использование свойств синуса и косинуса.
|
Примеры использования ограниченности функций.
|
§12. п.12.4., № 12.23(б), 12.25(г), 12.26(а)
|
1 час
|
|
|
|
§14. Системы уравнений с несколькими неизвестными.
|
|
|
8 часов
|
П. 14.1.
|
Урок108
|
|
Равносильность систем
|
Основные понятия. Решение системы двух уравнений с двумя неизвестными. Решение системы трех уравнений с тремя неизвестными. Несовместность системы. Равносильность систем уравнений. Простейшие утверждения о равносильности систем уравнений. Метод подстановки. Линейные преобразования систем.
|
§13. п.13.1., № 13.7(а),13.8(б), 13.9(г)
|
2 часа
|
Урок109
|
|
§13. п.13.1., № 13.11(а), 13.13(а),13.114(б)
|
П. 14.2
|
Урок110
|
|
Система-следствие
|
Основные понятия. Приведение подобных. Возведение в четную степень. Освобождение от знаменателей. Потенцирование. Применение формул.
|
§13. п.13.2., № 13.20(б), 13.21(в)
|
2 часа
|
Урок111
|
|
§13. п.13.2., № 13.23(в), 13.24(а), 13.26(а)
|
П.14.3
|
Урок112
|
|
Метод замены неизвестных.
|
Метод замены неизвестных. Примеры.
|
§13. п.13.3., № 13.28(г), 13.30(а),13.32(б)
|
2 часа
|
Урок113
|
|
§13. п.13.3., № 13.33(а), 13.36(а)
|
П.14.4
|
Урок114
|
|
Рассуждения с числовыми значениями при решении систем уравнений
|
Примеры нестандартных методов решения уравнений и неравенств.
|
§13. п.13.4., № 13.39(б), 13.40(б), 13.43
|
1 час
|
|
Урок115
|
|
Контрольная работа № 7 по теме:
|
«Использование свойств функций при решении уравнений и неравенств. Системы уравнений с несколькими неизвестными».
|
Повторить теорию
|
1 час
|
|
|
|
§15. Уравнения и неравенства с параметрами.
|
|
-
|
4 часа
|
П.15.1.
|
Урок116
|
|
Анализ контрольной работы. Уравнения с параметром.
|
Понятие уравнения с параметрами. Равенство с параметрами. Решение уравнений с параметрами
|
§14. п.14.1., № 14.4(б), 14.5(в), 14.6(в), 14.8(а)
|
1 час
|
П.15.2.
|
Урок117
|
|
Неравенства с параметром.
|
Решение неравенств с параметром.
|
§14. п.14.2., № 14.12(б), 14.15(в), 14.18(а), 14.20(б), 14.22(а)
|
1 час
|
П.15.3.
|
Урок118
|
|
Системы уравнений с параметром.
|
Решение систем уравнений с параметром.
|
§14. п.14.3, № 14.24(б), 14.25(а), 14.28(б)
|
1 час
|
П.15.4.
|
Урок119
|
|
Задачи с условиями.
|
Решение задач с условиями.
|
§14. п.14.4, № 14.33(а), 14.35(б), 14.39(а)
|
1 чаа
|
|
|
|
Повторение
|
|
Задания для повторения (стр. 393-416)
|
17 часов
|
|
Урок120
|
|
Повторение курса алгебры и математического анализа за 10-11 класс. Подготовка к итоговой контрольной работе.
|
Повторение курса алгебры и математич. анализа за 10-11 класс.
|
№ 37, 69, 201
|
13 часов
|
Урок121
|
|
Повторение курса алгебры и математич. анализа за 10-11 класс.
|
№ 181, 205,226
|
Урок122
|
|
Повторение курса алгебры и математич. анализа за 10-11 класс.
|
№ 206, 219, 262(б)
|
Урок123
|
|
Повторение курса алгебры и математич. анализа за 10-11 класс.
|
№ 54, 70, 253
|
Урок124
|
|
Повторение курса алгебры и математич. анализа за 10-11 класс.
|
№ 200(а), 204(в),222(в)
|
Урок125
|
|
Повторение курса алгебры и математич. анализа за 10-11 класс.
|
№ 212(б), 241(а)
|
Урок126
|
|
Повторение курса алгебры и математич. анализа за 10-11 класс.
|
№ 229(а), 259
|
Урок127
|
|
Повторение курса алгебры и математич. анализа за 10-11 класс.
|
№ 184, 197(в),234
|
Урок128
|
|
Повторение курса алгебры и математич. анализа за 10-11 класс.
|
№ 88,117, 196
|
Урок129
|
|
Повторение курса алгебры и математич. анализа за 10-11 класс.
|
№ 13, 28, 118
|
Урок130
|
|
Повторение курса алгебры и математич. анализа за 10-11 класс.
|
№ 22(в,д), 74, 145
|
Урок131
|
|
Повторение курса алгебры и математич. анализа за 10-11 класс.
|
№ 131, 140,210
|
Урок 132
|
|
Подготовка к итоговой контрольной работе.
|
Повторить теорию, формулы.
|
|
Урок 133-134
|
|
Итоговая контрольная работа № 8.
|
Итоговая контрольная работа.
|
Повторить теорию
|
2 часа
|
|
Урок135
|
|
Анализ итоговой контрольной работы
|
|
Повторить теорию
|
1 час
|
|
Урок136
|
|
Обобщение курса алгебры и начала анализа
|
|
Повторить теорию
|
1 час
|
|
|
|
|
|
Итого:
|
136 часов
|
 Скачать 0.61 Mb.
Скачать 0.61 Mb.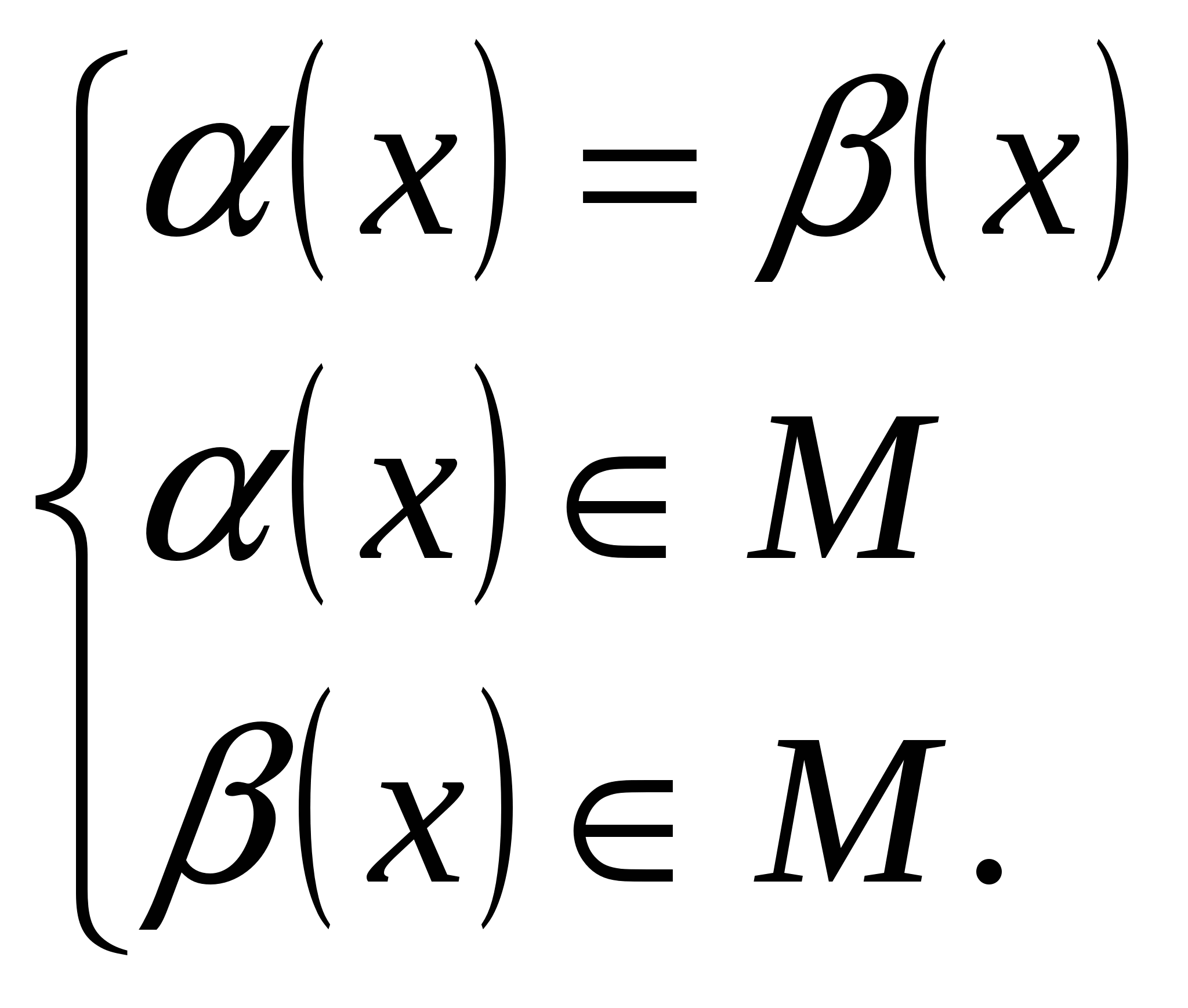 .
.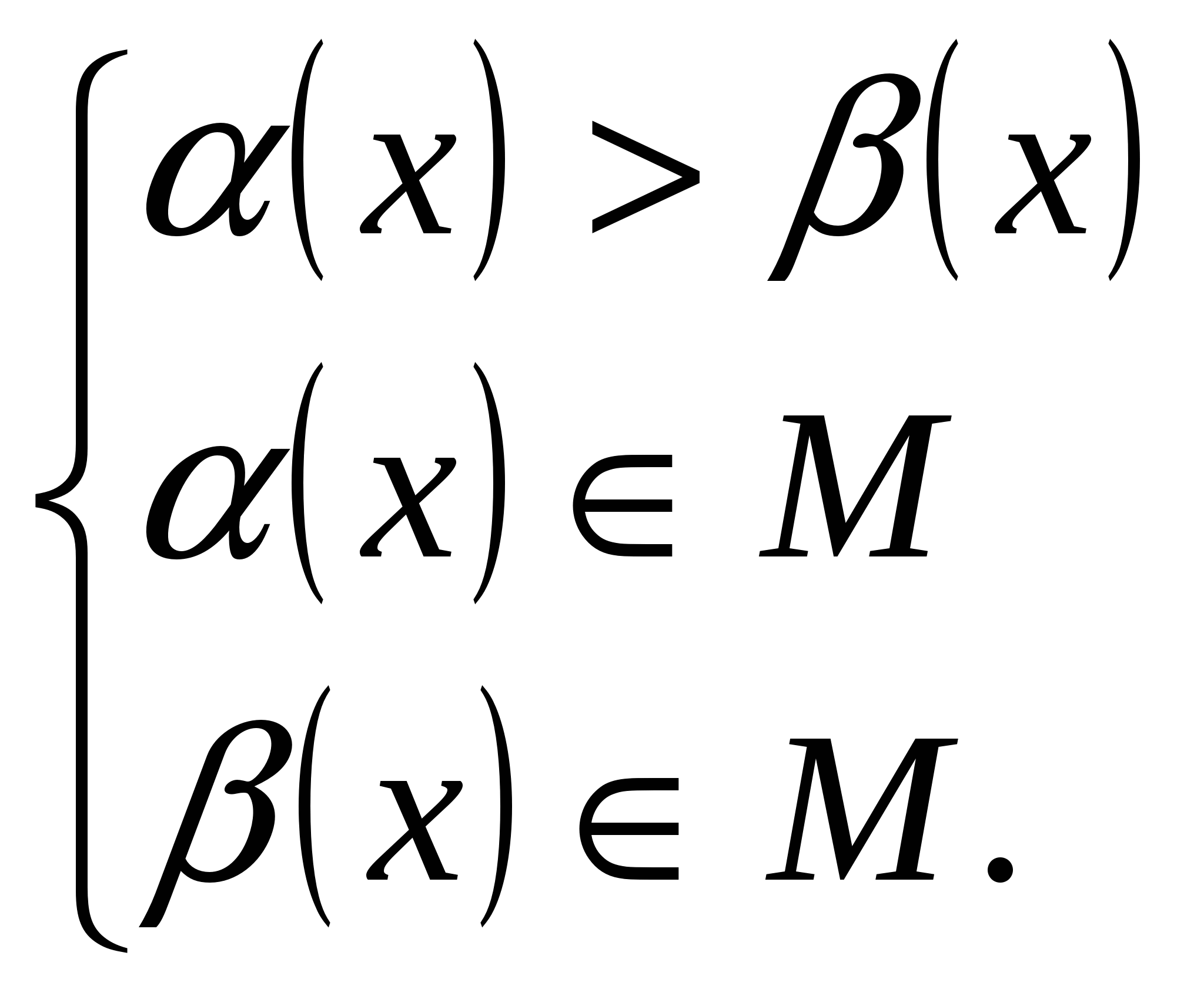 и
и 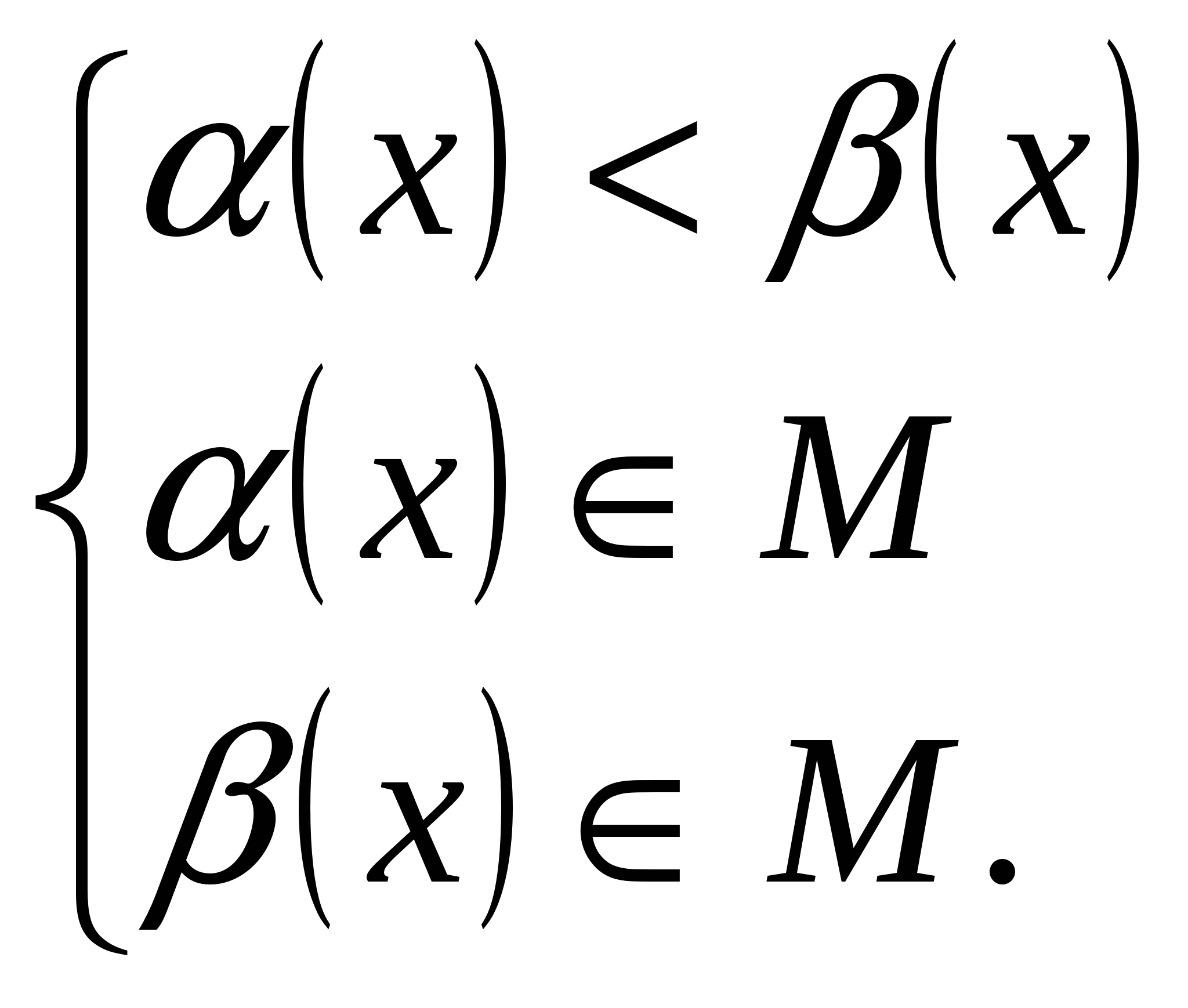 . Частный случай теоремы.
. Частный случай теоремы.