Цель Показать многогранность применения линейной функции в различных сферах человеческой деятельности. Показать связь алгебры и геометрии. Развитие интереса к математике. Воспитание целостного образа научного знания. Ход урока
| Линейная функция и её график. Цель
Ход урока: I. Мотивация. 7-й класс – самый необычный, самый интересный год изучения математики. Ценен, важен и интересен он тем, что здесь вы познакомились с двумя областями математической науки: алгеброй и геометрией.
Алгебраические и геометрические способы решения задач переплетаются, словно ветви дерева. Попробуем проследить и исследовать тесное сотрудничество алгебры и геометрии. II. Историческая справка. 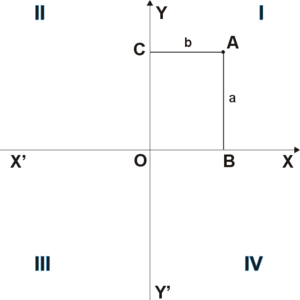 Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X'X и Y'Y. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление. В правосторонней системе координат положительное направление осей выбирают так, чтобы при направлении оси Y'Y вверх, ось X'X смотрела направо. Четыре угла (I, II, III, IV), образованные осями координат X'X и Y'Y, называются координатными углами или квадрантами (см. рис. 1). Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости. Функция — математическое понятие, отражающее связь между элементами множеств. Более точно, это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений). Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Функция может быть задана различными способами:
Цель урока заключаться в том, чтобы увидеть, как известная нам линейная функция находит свое применение в различных областях деятельности человека. III. Актуализация знаний.Две переменные x и y связаны функциональной зависимостью, если для каждого значения одной из них можно получить по определенному правилу одно или несколько значений другой.
Переменная, значения которой заданы, называется аргументом или независимой переменной; другая переменная, значения которой находятся по определённому правилу – называется функцией. Аргумент обычно обозначается через x, а функция – через y. Если каждому значению аргумента соответствует только одно значение функции, то эта функция называется однозначной Линейная функция — функция вида y = kx + b(для функций одной переменной). Основное свойство линейных функций: приращение функции пропорционально приращению аргумента. То есть функция является обобщением прямой пропорциональности. График линейной функции является прямой линией, с чем и связано ее название.
IV. Следующие задания более сложные.
Итак, называем еще одну область применения линейной функции. (Геометрия). И в данном случае мы познакомились с новым разделом математики V. Применения линейной функции. Работа в группах:
1 группа. (Физика). Велосипедист движется со скоростью 10км/ч. Записать формулу его пути S за время движения t. Построить график движения на первых тридцати километрах пути. 2 группа. (Метеорология). При начале нагревания вода в кипятильнике имела температуру 60C. При нагревании температура воды повышалась каждую минуту на 20 C. Найдите формулу, выражающую изменение температуры T воды в зависимости от времени t её нагревания. Будет ли функция T(t) линейной? 3 группа. (Геометрия) Одна сторона прямоугольной детской площадки равна X, другая – на 3 м больше. Выразите через X периметр P и площадь S этого прямоугольника. Найдите значение каждой функции P(X) и S(X) при X=6. При каком значении X периметр будет равен 46 м. 4 группа (Экономика) На складе было 300 т угля. Ежедневно на склад привозили ещё по 40 т. Выразить формулой зависимость количества угля p (в тоннах), находящегося на складе, от времени (в днях). Итак, обобщая все выступления мы приходим к выводу … Во многих сферах деятельности человека встречаются процессы, которые можно описать с помощью линейной функции. Разобраться в этом поможет ваша проектная деятельность. Предлагаю в качестве домашнего задания: Составить новую задачу о применении линейной функции в той отрасли знаний
|
 Скачать
Скачать