













 Министерство образования Московской областиГБОУ СПО «МОКИТЭУ» МО Автор разработки:Шакина Татьяна Ивановна
Министерство образования Московской областиГБОУ СПО «МОКИТЭУ» МО Автор разработки:Шакина Татьяна Ивановна–
преподаватель математикиТема: «Показательная функция,её графики и свойства» Методическая разработка урока по дисциплине: «Математика»Ликино-Дулево2013гОбщие сведения об урокеПреподаватель: Т.И. Шакина
Группа: 613
Специальность: 190631 Техническое обслуживание и ремонт автомобильного транспорта
Тема урока: «Показательная функция, её график и свойства»
Цель занятия:
Знать определение и свойства показательной функции;
Прививать умение читать свойства функции по её графику;
Знать рациональные приёмы построения графиков;
Знать схематичное изображение графика показательной функции;
Углубить знания о показательной функции.
Задачи занятия:
образовательная – углубить знания о показательной функции, продолжать прививать умение читать свойства функций по их графикам;
развивающая – формировать современное мировоззрение, показать широкое использование показательной функции;
воспитательная – развитие мыслительных операций (анализ, обобщение, применение дедуктивных рассуждений), знание рациональных приёмов построения графиков и их грамотного оформления.
Тип урока: Урок изучения нового материала.
Вид урока: Комбинированный.
По применяемым технологиям: иллюстративно-объяснительные, компьютерные (новые информационные) технологии обучения, технология проблемного обучения, педагогическая технология на основе системы эффективных уроков.
Используемые средства обучения: ПК, мультимедиапректор, графики показательной функции.
Раздаточный материал: опорный конспект.
Ожидаемые результаты:Обучающийся должен: Ход занятия.
Организационный момент.
Сообщить тему и цели занятия.
Актуализация знаний учащихся.
Фронтальная работа с классом – теоретический опрос по вопросам.
Раскрыть следующие понятия.
Вопросы учащимся.
|
Ответы.
|
Функция.
|
1.Если каждому значению переменной x поставить в соответствие единственное значение переменной y, то говорят, что задана функция
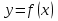 ; переменную x называют независимой переменной, переменную y называют зависимой переменной. ; переменную x называют независимой переменной, переменную y называют зависимой переменной.
|
Область определения функции.
|
2. Все значения, которые принимает независимая переменная x, образуют область определения.
|
Множество значений функции.
|
3.Все значения, которые принимает функция 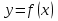 при значениях независимой переменной х из области определения, образуют множество значений функции . при значениях независимой переменной х из области определения, образуют множество значений функции .
|
Четность и нечётность функции.
|
4. Функция 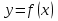 называется чётной, если для любого х из области определения функции выполняется равенство называется чётной, если для любого х из области определения функции выполняется равенство 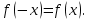
Функция 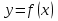 называется нечётной, если для любого х из области определения функции выполняется равенство называется нечётной, если для любого х из области определения функции выполняется равенство 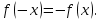
|
Способы задания функции.
|
5.Функцию можно задать аналитически (с использованием формулы), таблично, в системе координат в виде графика функции.
|
Нули функции.
|
6. Нули функции – это значения независимой переменной х из области определения, при которых значения функции равны нулю.
|
Монотонность функции.
|
7.Функция 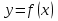 называется строговозрастающей, если для любых называется строговозрастающей, если для любых 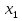 и и 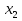 из области определения функции, таких что из области определения функции, таких что 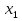 < < 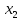 выполняется неравенство выполняется неравенство 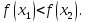
Функция 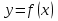 называется строгоубывающей, если для любых называется строгоубывающей, если для любых 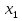 и и 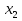 из области определения функции, таких что из области определения функции, таких что 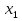 < < 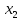 выполняется неравенство выполняется неравенство 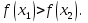
|
Простейшие преобразования графиков функций (вертикальный сдвиг, горизонтальный сдвиг).
|
8. Вертикальным сдвигом называется график функции 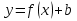 , полученный преобразованием графика функции , полученный преобразованием графика функции 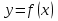 параллельным переносом вдоль оси Оу; если параллельным переносом вдоль оси Оу; если  . .
Горизонтальным сдвигом называется график функции 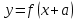 , полученный преобразованием графика функции , полученный преобразованием графика функции 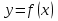 параллельным переносом вдоль оси Ох; если параллельным переносом вдоль оси Ох; если 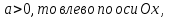
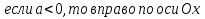 . .
|
Изучение нового материала, формирование знаний, умений и навыков.
 Скачать 341.22 Kb.
Скачать 341.22 Kb.














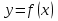 ; переменную x называют независимой переменной, переменную y называют зависимой переменной.
; переменную x называют независимой переменной, переменную y называют зависимой переменной.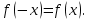
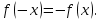
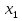 и
и 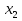 из
из 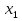 <
< 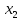 выполняется неравенство
выполняется неравенство 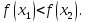
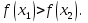
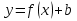 , полученный преобразованием графика функции
, полученный преобразованием графика функции  .
. 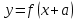 , полученный преобразованием графика функции
, полученный преобразованием графика функции 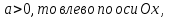
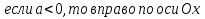 .
.