Открытый урок по алгебре в 10 классе Тема урока: «Решение логарифмических уравнений» Урок подготовила и провела: учитель математики мбоу сош №18
 Скачать 68.81 Kb. Скачать 68.81 Kb.
|
| Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №18 Открытый урок по алгебре в 10 классе Тема урока: «Решение логарифмических уравнений» Урок подготовила и провела: учитель математики МБОУ СОШ №18 Головина Н.А. 2014 год пос. Высокий План урокаТема урока: «Решение логарифмических уравнений» Тип урока: урок применения знаний на практике. Форма урока: урок-практикум. Цели урока: 1. Закрепить навыки решения логарифмических уравнений. Уметь использовать их решение при подготовке к ЕГЭ. Задачи урока:
2. Формировать практические навыки решения логарифмических уравнений на основе изученного теоретического материала. 3. Развивать познавательный интерес к обучению. Оборудование: интерактивный комплекс, Интернет-ресурсы. Ход урока 1. Организационный момент «Уравнение – это золотой ключ, открывающий все математические сезамы». Современный польский математик С. Коваль. 2. Проверка домашнего задания 3.Устная работа (с использованием презентации) а)Найдите значение выражения: б) Заполни пропуски: а)Log2 16 = …; б)Log2 1/8 = …; в) Log2 1 = …; г)Log√5 25 = …; д)Log…1/32 = - 5. в)Решите уравнение: log3x=4 log2(x+1)=3 logх16=2 г)Сформулируйте методы решения логарифмических уравнений: а) По определению логарифма. б) Потенцирование (переход от логарифма данного выражения к самому этому выражению). в) Введение новой переменной. г) Логарифмирование обеих частей уравнения. д) Приведение к одному основанию. д) Функционально-графический метод. 4. Закрепление навыков решения логарифмических уравнений. Этапы решения уравнения:( проговорить ) а) Найти область допустимых значений (ОДЗ) переменной б) Решить уравнение, выбрав метод решения в) Проверить найденные корни непосредственной подстановкой в исходное уравнение или выяснить, удовлетворяют ли они условиям ОДЗ (По каждому методу решаем уравнения у доски с пояснениями- 5 человек) Условия на слайдах Решение уравнений разными методами (Работа на доске) 1.log х+1(2x2+1)=2 По определению логарифма имеем: 2х2+1=(х+1)2, X2 -2x=0 x=2 или x=0. Проверка: х=0 не может быть корнем данного уравнения, так как основание логарифма х+1≠1. При х=2 log 2+1( 2•22 +1)=log39=2. Ответ: 2. 2. log 5 x=log 5 (6-x2 ) Из равенства логарифмов следует: x= 6- x2 x2-x-6=0; D=25 x=-3 или x=2. Проверка: x=-3 корнем уравнения быть не может, так как логарифмы отрицательных чисел не существуют. Log5 x=log52, Log5(6-x2) = log5 (6-22)=log5 2. Ответ: 2. 3. lg2 x3 - 10lgx + 1=0 Приведём уравнение к квадратному: Т.к. lg2 x3=(lgx3)2=(3lgx)2= 9lg2 x, то 9lg2 x - 10lgx+1=0. Пусть lg x=y, тогда 9y2- 10y+1=0; D=64 y=1 или y=1/9 lgx=1 или lgx=1/9 x=10 или х=10 1/9. Проверкой подтверждаем, что оба числа являются корнями. Ответ: 10; 10 1/9 4. X lgх+2= 1000 Логарифмируя обе части уравнения ( x > 0), получим: ( lgx+2)•lgx=lg1000 Lg2 x+ 2lgx- 3=0 lgx=y у2+ 2у- 3=0 y=- 3, у=1. lgx=- 3, x=10-3=0,001; lgx=1, x=10 Выполнив проверку, убедимся, что оба найденных значения переменной являются корнями данного уравнения. Ответ: 0,001; 10. 5. Log16 x+log4 x+ log2 x=7 (1/4)log 2x+ (1/2)log 2x+ log 2x=7 (7/4)log 2x=7 Log 2x=4 x=16. Ответ: 16. 6. Найти корни уравнения Log 3x=4-x Так как функция у= log 3 х возрастающая, а функция у =4-х убывающая на (0; + ∞ ),то заданное уравнение на этом интервале имеет один корень. Ответ: 3 5. Закрепление знаний Учащиеся решают задания с последующей самопроверкой: I.Решите уравнение: Пример 1 Пример 2 Пример 3 Пример 4 6. Самостоятельная работа с последующей самопроверкой
Ответы:
7.Физкультминутка Обучающиеся выполняют комплекс упражнений, укрепляющие мышцы спины и позвоночник, что позволяет снять напряжение и сохранить осанку. 8. Компьютерное тестирование (самопроверка знаний) по теме «Решение логарифмических уравнений ». Работа за компьютерами. Использование единой коллекции федеральных цифровых образовательных ресурсов (Интернет-ресурсы). После завершения тестирования учащиеся проверяют результаты на компьютере. 9. Подведение итогов урока. Рефлексия. Продолжите фразу:
10. Домашнее задание Индивидуальные задания по теме: «Решение логарифмических уравнений» из открытого банка ЕГЭ 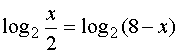 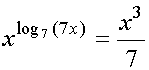 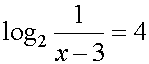 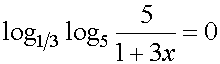 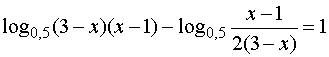 | ||||||||||||||||||||||||||||||||||||||||||||||||||||