Решение уравнений в электронных таблицах Найти в электронных таблицах корень уравне­ния

Скачать 46.4 Kb. Название Решение уравнений в электронных таблицах Найти в электронных таблицах корень уравне­ния Дата 11.03.2016 Размер 46.4 Kb. Тип Решение

Исследование математических моделей Приближенное решение уравнений в электронных таблицах Найти в электронных таблицах корень уравне­ния х - sinx = 0 приближенными методами (графическим и численным). В электронных таблицах Microsoft Excel определим корни уравнения х - sinx = 0. Сначала гра­фически, путем построения диаграммы типа График, и за­тем приближенно с заданной точностью с помощью метода Подбор параметра. Графическое решение уравнения. Для графического ре­шения уравнения представим функцию у = х - sinx в таб­личной форме. В диапазон ячеек В1:Р1 (рис. 3.17) ввести значения ар­гумента функции от -1,4 до 1,4 с шагом 0,2. В ячейку В2 ввести формулу вычисления значений функции =B1^3-SIN(B1) и скопируем ее в диапазон яче­ек С2:Р2. А В С D Е F G Н I J К L М N О Р 1 X -1,4 -1,2 -1,0 -0,8 -0,6 -0,4 -0,2 0,0 0,2 0.4 0,6 0.8 1,0 1.2 1,4 2 y=x3-sinx -1.8 -0,8 -0,2 0.2 0,3 0,3 0,2 0,0 -0,2 -0,3 -0,3 -0,2 0,2 0.8 1,8 Табличное представление функции у = х3 — sinx Для грубо приближенного определения корней уравне­ния необходимо построить диаграмму типа График. График функции пересекает ось X три раза и, следова­тельно, уравнение имеет три корня (рис. 3.18). 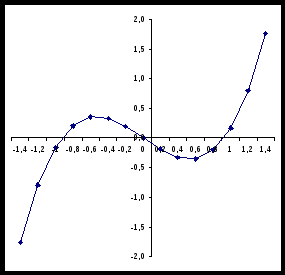По графику приближенно можно определить, что Приближенное решение уравнения с использованием метода Подбор параметра. Возможности электронных таб­лиц не ограничиваются вычислениями по формулам и по­строением диаграмм и графиков. В электронных таблицах Microsoft Excel имеется надстройка Подбор параметра. Надстройка Подбор параметра позволяет задать значе­ние функции и найти значение аргумента функции, кото­рый обеспечивает требуемое значение функции. При подбо­ре параметра изменяется значение в ячейке аргумента функции до тех пор, пока в ячейке самой функции не по­явится требуемое значение. Используем метод Подбор параметра для поиска при­ближенного решения уравнения у = х3 - sinx с заданной точностью. Установить точность определения корней уравнения можно путем установки в ячейках таблицы необходи­мой точности представления чисел (например, три знака после запятой). Начнем с поиска более точного значения наименьшего корня. По графику видно, что ближайший аргумент к точке пересечения оси X графиком функции ра­вен -1,0. По таблице значений функции мож­но определить, что этот аргумент функции хранится в ячей­ке D1. Теперь используем метод Подбор параметра и опреде­лим значение аргумента х (ячейка D1), при котором значе­ние функции у (ячейка D2) равно нулю. Выделить ячейку D2 со значением функции и введем команду [Сервис-Подбор параметра...]. В диалоговом окне Подбор параметра в поле Значение: ввести требуемое значение функции (в данном случае 0). В поле Изменяя значение ячейки: ввести адрес ячейки $D$1, в которой будет производиться подбор значения аргумента. Щелкнуть по кнопке ОК. В окне Результат подбора параметра будет выведена информация о величине подбираемого и подобранного значения В ячейке аргумента D1 появится подобранное значение -0,929. 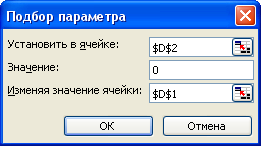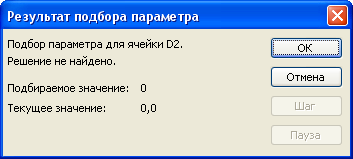Таким образом, корень уравнения Самостоятельно Аналогичным образом найти более точные значения для других корней уравнения. Ответ: