Неполные квадратные уравнения
 Скачать 43.55 Kb. Скачать 43.55 Kb.
|
| Урок алгебры в 8 классе. Тема: Неполные квадратные уравнения. Цели урока: сформировать умения, навыки решения неполных квадратных уравнений. расширить знания учащихся по данной теме. развивать математическую логику, прививать интерес к изучению математики путем дружеского соперничества в группах. Оборудование. Карточки с заданиями, плакат с эпиграфом урока: В класс вошел – не хмурь лица! Будь веселым до конца. Ты не зритель, и не гость, Ты программы нашей гвоздь. Не ломайся, не кривляйся, Всем законам подчиняйся. Структура урока.
Разъяснение целей учебной деятельности учащихся и правил игры. Мотивационная заставка – чтение эпиграфа.
Вопросы учащимся:
1) Цепочка. Учащиеся каждой группы получают задания и передают сидящему сзади. Побеждает та группа, которая заработает больше очков, за самое короткое время. Задание проверяет жюри. Если задание было выполнено быстро и правильно, то команда получает дополнительно 5 баллов. Задание: решите уравнения. 1 . 1,8 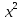 = 0 = 02. 2 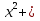 6х = 0 6х = 03. 3 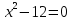 4. 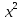 + 2х – 3 = 2х + 6 + 2х – 3 = 2х + 65. 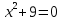 Учитель: Какие уравнения у вас вызвали затруднения? Давайте объясним их решения. 2) Задание всему классу: составьте и решите квадратные уравнения, записанные на доске. 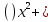 ( )х = 0 ( )х = 0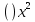 + ( ) = 0 + ( ) = 0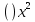 = ( ) = ( )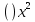 = 0. = 0.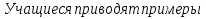 . Каждая группа защищает решение уравнения. . Каждая группа защищает решение уравнения. 3) Турнир математических терминов «Грамотей». Записать ответ данного предложения или вопроса в виде математического термина. Группа совещается 1-2 минуты, а затем выдвигает «грамотея» и он записывает слова на доске.
4) Учитель. Степа Смекалкин, не решая уравнения вида а 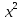 + с = 0, сразу говорит имеет оно корни или нет. А вы можете это сделать? + с = 0, сразу говорит имеет оно корни или нет. А вы можете это сделать?Уравнения записаны на доске 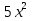 + 6 = 0 + 6 = 0-2 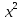 - 3 = 0 - 3 = 04 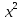 - 3 = 0 - 3 = 0-7 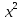 + 2 = 0 + 2 = 0(Если сразу не отвечают, то пусть решают, а затем делают вывод.) Вывод: Если числа «а» и «с» одинакового знака, то уравнение не имеет корней. Если числа «а» и «с» разного знака, то уравнение имеет корни. 5) Учитель. Приведите примеры уравнений вида а 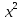 +с = 0 +с = 0- не имеющих корней; - имеющие корнями дробные числа; - имеющие корнями иррациональные числа. 6).Самостоятельная работа.
7) Дополнительное задание. А)Решить уравнения, записанные на карточках. Решают по одному человеку от группы.
Б) «Кто любит учиться –никогда не проводит время в праздности» Автора этих слов вы узнаете, разгадав шифрограмму.
1) 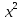 = 81 4) = 81 4)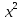 = - 2 7) = - 2 7)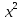 -1 = 0 -1 = 02) 2 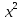 -8 = 0 5) -8 = 0 5)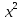 - 3х = 0 8) - 3х = 0 8)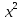 = 9/4 = 9/43) 5 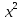 = 0 6) = 0 6)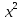 = 1,21 9) = 1,21 9) 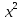 + х = 0 + х = 0Шарль Луи Монтескье (французский просветитель, правовед, философ) 4. Домашнее задание. 5. Итог урока. Вернуться к эпиграфу. Сравнить свое выражение лица с первоначальным. Оценить работу групп. Что нового и полезного узнали из урока? Литература. 1.Контрольно-измерительные материалы по алгебре для 8 класса. Москва,2010г. 2.Учебник алгебра -8 .Ш.А. Алимов, Ю.М.Колягин, Москва,2009г. 3.Дидактические игры на уроках математики. В.Г.Коваленко, Москва, «Просвещение», 1990г. 4.Дидактические материалы . Москва, «Просвещение»,2003г. |
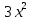 = 0
= 0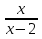 = 0
= 0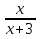 = 0
= 0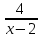 = 0
= 0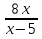 = 0
= 0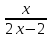 = 0
= 0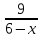 = 0
= 0