|
Понятие вектора 2-ой урок
                                   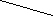                                   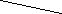   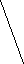    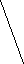                          Тема урока: Понятие вектора 2-ой урок Тема урока: Понятие вектора 2-ой урок
Цель: создать условия для работы учащихся над понятиями и их определениями (определение вектора, изображение и обозначение вектора, определение нулевого вектора, длины (модуля) вектора, коллинеарных векторов; сонаправленных, противоположнонаправленных векторов; равных, противоположных векторов) и для овладения действием откладывания вектора от данной точки, закрепить эти понятия и определения (с этими понятиями ученики ознакомились на предыдущем уроке).
Организация работы
Класс разбивается на группы по 4 человека. (Для того, чтобы обеспечить одинаковый темп работы учащихся в группе, в каждую группу входят учащиеся приблизительно одного уровня подготовленности.) группа обеспечивается 4-мя карточками.
Карточка № 1
1 часть
|
2 часть
|
Что называется вектором?
|
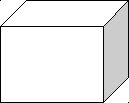
На предложенных рисунках укажите векторы:
а) б) в)
г) д) е)
|
Цель: создать условия для выполнения учащимися действия подведения объекта под понятие. (Отнесение объекта к тому или иному понятию предполагает установление наличия у этого объекта признаков данного понятия, достаточных или необходимых и одновременно достаточных)
|
Как обозначается и изображается вектор?
|
а) Запишите изображенные векторы:
В
М
А С
→ → → → →
б) Постройте векторы: АА1, ВА, В1D, МС, АМ,
→ → →
В1А1, А1В1, D1D
B1 M C1
А1 D1
B C
A D
|
Цель: учить изображать и обозначать векторы, используя фигуры как на плоскости, так и в пространстве
|
Карточка № 2
1 часть
|
2 часть
|
Какой вектор называется нулевым?
|
Перечислите и запишите нулевые векторы:
А В
М
D С
|
Дайте определение длины (модуля) вектора
|
а) Найдите и запишите длины изображенных векторов:
K С
1
А В
2
D
б) Начертите вектор, длина которого равна 3 см.
в) Начертите вектор, длина которого равна 0.
г) Дано: /а/ = k. Какие значения может принимать k?
|
Цель: 1) учить находить и записывать длину вектора по рисунку, если указана единица измерения отрезков (2а);
2) учить по заданной длине изображать вектор (2 б,в);
3) обобщить, какие значения может принимать длина вектора (2 г).
|
Карточка № 3
1 часть
|
2 часть
|
Сформулируйте определение коллинеарных векторов
|
а) Укажите на рис. коллинеарные векторы:
е а М
с b k m
б) Начертите два вектора которые являются коллинеарными и два вектора, которые не являются коллинеарными.
|
Какие вектора называются сонаправленными?
|
2.Запишите сонаправленные векторы:
b d K
n c
f
|
Цель: создать условия для выполнения учащимися действия подведение объекта под понятие
|
Карточка № 4
1 часть
|
часть
|
1. Сформулируйте определение противоположнонаправленных векторо
|
1. Укажите на рис. Противоположнонаправленные векторы и запишите их:
e m D n
a b c
|
2.Какие векторы называются равными?
|
2. Выпишите равные векторы:
B C
а) б) B C
O
A D A D
в) A1 B1
D1 C1
A B
D C
г) От точки М отложите векторы, равные данным
а М
с е
|
Цель: создать условия для выполнения учащимися действий подведение объектов под понятие
|
Алгоритм работы
Выполните самостоятельно задания обеих частей карточки (сформулируйте определение, решение практического задания запишите в тетради).
Закончив работу над карточкой, отчитайтесь перед учителем или консультантом (первичный контроль).
Отыщите партнера по схеме (см. ниже).
Поменяйтесь карточками.
Проверьте друг у друга определения, указанные в первой части новой карточки.
Выполните в тетради задания второй части полученной карточки и организуйте взаимоконтроль.
Оцените ответ друг друга и заполните листок учета (см. ниже).
Ищите нового партнера по схеме.
Алгоритм работы повторяется с п.4. Работа закончена, если выполнены задания всех 4-х карточек.
Выходной контроль.
Замечание: если перед обменом карточками, партнер еще не готов к работе в паре, то ученику рекомендуется выполнить дополнительные задания, к своей карточке
Маршрут движения
1 ↔ 2 1 2 1 ↔ 2 1 2
↕ ↕ ↕ ↕
3 ↔ 4 3 4 3 ↔ 4 3 4
Листок учета
|
Карточка № 1
|
Карточка № 2
|
Карточка № 3
|
Карточка № 4
|
Кто проверял
|
|
|
|
|
Отметка о выполнении
|
а)
б)
|
а)
б)
|
а)
б)
|
а)
б)
|
Формы выходного контроля:
Фронтальный контроль в группе, осуществляемый учителем или консультантом.
Контроль по номеру карточки внутри группы или класса.
Защита в группах выполненных заданий.
Математический диктант по отработанным определениям.
|
|
|
 Скачать 55.09 Kb.
Скачать 55.09 Kb.
























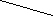


































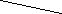


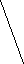



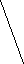
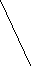


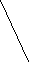




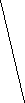


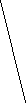












 Тема урока: Понятие вектора 2-ой урок
Тема урока: Понятие вектора 2-ой урок