Межпредметные связи математики и естественных наук
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
| Межпредметные связи математики и естественных наук Предметы естественно-математического цикла дают учащимся знания о живой и неживой природе, о материальном единстве мира, о природных ресурсах и их использовании в хозяйственной деятельности человека. Общие учебно-воспитательные задачи этих предметов направлены на формирование диалектико-материалистического мировоззрения, политехнических знаний и умений учащихся, всестороннее гармоническое развитие личности. На основе изучения общих законов развития природы, особенностей отдельных форм движения материи и их взаимосвязей учителя формируют у учащихся современные представления о естественнонаучной картине мира. Изучение всех предметов естественнонаучного цикла взаимосвязано с математикой. Математика дает учащимся систему знаний и умений, необходимых в повседневной жизни и трудовой деятельности человека, а также важных для изучения смежных дисциплин (физики, химии, черчения, трудового обучения и др.). Основные взаимосвязи предметов естественно-математического цикла 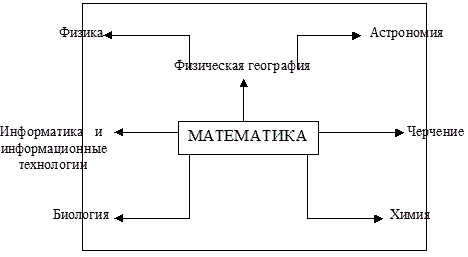 На основе знаний по математике у учащихся формируются общепредметные расчетно-измерительные умения. Изучение математики опирается на преемственные связи с курсами физики, химии, информатики, биологии, экономики. При этом раскрывает практическое применение получаемых учащимися математических знаний и умений, что способствует формированию у учащихся научного мировоззрения, представлений и математическом моделировании как обобщенном методе познания мира. Моделирование как метод познания включает в себя: • построение, конструирование модели; • исследование модели(экспериментальное или мысленное); • анализ полученных данных и перенос их на подлинный объект изучения. Решая прикладные задачи, надо пройти названные выше три этапа: • построение модели (перевод условия задачи с обыденного на математический язык) • работа с моделью (решение уравнения, неравенства и т. д.) • ответ на вопрос задачи На примере таблицы1 можно проследить взаимосвязь между математикой и предметами естественно-математического цикла в изучаемых темах. Таблица 1
Осуществлять МПС возможно различными путями, способами и средствами, с помощью которых преподаватель создает условия для реализации взаимосвязанного, межпредметного обучения и соответствующим образом организует мыслительную деятельность учащихся. Выделяются следующие пути установления МПС: информационно-рецептивный, репродуктивный, исследовательский и проблемный. Дадим им подробную характеристику, рассмотрим некоторые особенности реализации при обучении математике, направления совершенствования. Любая информация может быть усвоена только в том случае, если она включается в систему ранее полученных знаний, а не является совершенно новой, неизвестной и несовместимой с предыдущим знанием. Для уточнения основных положений темы и включения их в уже сложившуюся систему знаний преподаватель использует дополнительные сведения из других дисциплин, осуществляя, таким образом, реализацию МПС через конкретизацию учебного материала с помощью элементов знаний других учебных предметов. МПС информационно-рецептурного характера могут осуществляться разными способами. Например, при обращении к учебному материалу ранее изученных дисциплин преподаватель напоминает учащимся пройденный материал, использует его как фундамент, что позволяет не тратить время на пересказывание изученного. Так, при решении на занятиях прикладных задач, использующих изученный учебный материал других дисциплин, преподавателю необходимо напомнить формулы и законы. Другим способом осуществления информационно-рецептурных связей является сообщение учебного материала смежной дисциплины. Это происходит, когда учащимся трудно восстановить в памяти положения, необходимые для раскрытия содержания учебного материала, или имеющиеся данные не соответствуют новым научным данным, или рассматриваемое явление изучалось ранее лишь частично. Сюда можно отнести справочные данные и необходимые для решения задачи формулы. Созданию положительного эмоционального фона способствуют иллюстрирование учебного материала: описание исторических событий, использование биографий выдающихся ученых, интересных научных фактов и т. п. Иллюстративный материал при этом преподаватель может черпать из смежных наук. Использование для иллюстрации элементов историзма повышает заинтересованность учащихся в изучении математики, вносит в занятия элемент занимательности, демонстрирует происхождение понятий математики из реальной жизни. Это искусство открытия, когда учащимся не навязывается готовое решение, а они сами ищут его, знаменует собой деятельностный подход, связанный с активным усвоением изучаемого материала. Репродуктивный путь является наиболее распространенным в общей системе обучения и широко используемым в преподавании математики. К числу репродуктивных способов относятся повторение, сравнение, закрепление, воспроизведение, применение, перенос и другие виды учебной деятельности. Для установления МПС преподаватель или сообщает новые сведения, или повторяет с ними пройденный материал других дисциплин. Повторение играет важную роль в построении смысловых ассоциаций между изученным материалом одной дисциплины и изучаемым в другой. Это дает возможность рассмотреть некоторые известные положения с разных сторон, помогает повысить самостоятельность и творческий потенциал учащихся, интерес к вопросу. Непосредственно в преподавании математики повторение учебного материала других дисциплин используется редко. Однако другие дисциплины очень часто повторяют пройденный математический материал. Большое значение имеет установление МПС путем сравнения учебного материала разных дисциплин. Сравнение знаний способствует развитию мыслительных способностей, обеспечивает осознанное усвоение знаний. Одной из важнейших целей обучения является выработка умений применять полученные знания в различных видах учебной деятельности. Сформированные умения и навыки будут в данном случае выступать, с одной стороны, как результат обучения, а с другой – как способ достижения этого результата. МПС здесь играют особую роль. Применение знаний из других дисциплин свидетельствует о наличии этих знаний, прочности их усвоения, о сформированности умений и навыков обращения к знаниям других дисциплин и достигнутом результате применения как критерии обученности. Эти умения и навыки формируются через использование прикладных задач в практике преподавания математики. МПС наиболее успешны, когда учащиеся самостоятельно применяют знания разных наук в учебной и практической деятельности. В этом случае особое значение приобретает отработка некоторых приемов переноса действий межпредметного свойства. В процессе формирования определенного навыка при изучении отдельной науки сложившиеся ассоциации могут быть перенесены на подобные виды деятельности при изучении других наук. Перенос межпредметного уровня может осуществляться только тогда, когда новые действия имеют достаточно общего с уже освоенными. При осуществлении МПС значительная роль принадлежит творческому началу, поэтому в практике преподавания математики широко используется исследовательский путь. Основной его чертой является организация деятельности преподавателей и учащихся, обеспечивающая решение новых творческих задач при изучении программного материала. Учащиеся при этом совершают самостоятельные поисковые мыслительные операции, направленные на исследование неизвестного для них способа решения учебной задачи. Способами реализации исследовательского пути установления МПС могут быть поисковые самостоятельные работы: обработка данных научной литературы, творческие задания (доклады на конференциях, курсовые работы и т. п.), научные исследования и др. Хорошие результаты в установлении МПС математики с другими дисциплинами достигаются при использовании проблемного пути. Он значительно оживляет деятельность учащихся за счет повышения уровня самостоятельности, активности и творчества. При решении учебных проблем включаемый в их содержание межпредметный материал разнообразит способы учебной и обучающей деятельности, повышает качественный уровень учебного материала. Наиболее распространенным способом реализации проблемного пути установления МПС является использование проблемной ситуации, проблемного вопроса, проблемного задания или проблемной задачи. Мышление начинается с появления проблемы, противоречия. Проблемная ситуация сигнализирует о недостаточности имеющихся у субъекта знаний для совершения познавательного акта. Возникновение условий, делающих необходимым привлечение знаний из других дисциплин, является одной из характерных черт проблемных ситуаций, которые возникают объективно, независимо от желания преподавателя и обусловлены закономерностями учебного процесса. При обучении математике проблемная ситуация межпредметного свойства возникает при решении прикладных задач на практических занятиях или создается преподавателем на занятии при изучении новой темы постановкой прикладной проблемы, через решение которой и осуществляется введение нового материала. Более глубокий уровень интеграции – совместные (интегрированные) уроки, которые проводятся одновременно двумя или более учителями. На таких уроках возможно рассмотрение комплексных вопросов, которые по самой своей сути требуют привлечения знаний из разных предметов. Главное достоинство этих уроков заключается в том, что они ориентированы на формирование мировоззрения учащихся на основе комплексного подхода к определению их содержания. Также немаловажно и уменьшение при этом учебной нагрузки школьников, устранение повторений материалов в разных предметах. Возможны совместные уроки по следующим направлениям: - математика и химия Межпредметные связи математики с химией имеют достаточно большие потенциальные возможности, основанные на математических моделях химических процессов. Кроме широко используемых в химии пропорций, процентных отношений и множества задач на смеси, решение задач с химическим содержанием предоставляет широкие возможности для построения математических моделей, использующих линейные уравнения, системы линейных уравнений, производную, интегралы, дифференциальные уравнения и т. д. Приведем несколько примеров таких моделей. Пример 1. Масса смеси карбонатов калия и натрия равна 7,64 грамма. После превращения карбонатов в нитраты масса смеси увеличилась до 11,48 грамма. Определить количество карбоната калия в смеси. Если через х обозначить количество граммов карбоната калия, то х удовлетворяет линейному уравнению: х/138 + (7,64 - х)/106 = 0,06 Пример 2. Газовая смесь состоит из окиси азота NO и кислорода O2. Требуется найти концентрацию O2, при которой содержащаяся в смеси окись азота окисляется с наибольшей скоростью. Скорость реакции 2NО + O2 = 2N O2 выражается формулой V = Kx2y. Здесь х - концентрация NO (в процентах), у - концентрация O2 (в процентах), К -константа. Тогда у = 100 - х; и V =Кх2 (100 -х), 0 ≤ х ≤ 100. Наибольшая скорость реакции будет в том случае, когда V'(х) = 0, то есть х = 66,67 %. Как показывают рассмотренные примеры, потенциальные возможности межпредметных связей между математикой и химией довольно обширны и многообразны и задача учителя - использовать их при изучении химии и математики, а задача ученых-методистов - вооружить учителя необходимыми дидактическими материалами. Прежде всего, следует отметить то, что при реализации межпредметной связи математики и химии обучение математике не должно быть подменено изучением химии на уроках математики, напротив, обучение математике должно быть усовершенствовано на основе примеров из химии, на основе целенаправленной систематической связи с химией через примеры и упражнения, содержание которых прямо или косвенно имеет отношение к химии. При этом возникает вопрос: «Каким должно быть содержание примеров и задач из курса химии, чтобы это, с одной стороны, вписывалось в обучение математике, а с другой стороны, - было направлено на реализацию межпредметной связи математики и химии?» Тут требуется специальный дидактический материал, который, к сожалению, отсутствует в действующих учебных пособиях по математике. Требование вариативности содержания обучения математике внутри профилей неизбежно приводит к построению курса по принципу инвариантного ядра и модульных дополнений, характеризующих профильную составляющую курса. В. А. Сластенин и др. подчеркивают, что: «...инвариантная часть (ядро) учебного плана обеспечивает приобщение к общекультурным и национально значимым ценностям... Вариативная (модульное дополнение) часть, учитывающая личные особенности, интересы и склонности учащихся, позволяет индивидуализировать процесс обучения. ...Эти взаимодополняющие... части... не являются полностью независимыми. В результате их пересечения выделяются три основных вида учебных занятий: - обязательные занятия, образующие базовое ядро общего среднего образования; - обязательные занятия по выбору учащихся; - факультативные занятия (необязательные занятия по выбору)». На занятиях по выбору выступает необходимость выявления межпредметных связей математики с большинством предметов школьного учебного плана. Действительно, содержание модульной составляющей связано с содержанием профильных курсов, которое невозможно учесть без установления связей математики с физикой, экономикой, биологией, химией и т. д. В основе системы межпредметных связей лежит фундаментальный принцип построения математических моделей изучаемых явлений. Использование в смежных науках аппарата математического моделирования позволит изучить его глубже, полнее, всестороннее. Именно эти положения составляют основу того, что сегодня называют межпредметными связями математики. Более того, сегодня мы в состоянии сопоставить те реальные ситуации, которые возникают в окружающем нас мире, с тем математическим аппаратом, который имеется у учеников общеобразовательной школы. Использование МПС при обучении математике выполняет следующие функции: способствует решению чисто учебных задач по закреплению базовых математических знаний, умений и навыков в процессе их постоянного применения в обучении разным предметам, являясь важным фактором совершенствования процесса обучения на всех его уровнях; позволяет закрепить профессионально значимые знания, умения и навыки и создать положительный эмоциональный фон обучения математике; повышает заинтересованность в изучении как математики, так и других дисциплин; помогает развивать мышление; способствует развитию значимых качеств личности; осуществляет интеграцию учебных дисциплин, показывая, как одни и те же законы применяются в различных научных отраслях; выстраивает единую научную картину мира и тем самым вносит вклад в формирование научного мировоззрения. Проблема реализации взаимосвязей между математикой и дисциплинами естественнонаучного, гуманитарного и экономического циклов решает глобальную задачу социализации личности, функциональной грамотности человека и его полноценного функционирования в современном быстро меняющемся мире. |