«Лист Мебиуса и бесконечность»
 Скачать 141.98 Kb.
|
| Конференция «Лист Мебиуса и бесконечность» Цель: рассмотреть лист Мебиуса и его свойства. Задачи: 1. выработка умений самостоятельно работать с дополнительной и справочной литературой по математике; 2. формирование позитивного отношение к математике и к ее изучению План конференции:
Ход конференции. Преподаватель: Сегодня мы познакомимся с удивительной поверхностью, которая имеет только одну сторону и относится к математическим неожиданностям. Свой знаменитый лист Мебиус придумал в 1858 году. Это поразительной красоты открытие было сделано, на первый взгляд, совершенно случайно. Так же, как согласно легендам, совершили свои великие открытия Ньютон и Архимед. Но, мы должны понимать, что сделать это так легко может только человек увлеченный наукой, имеющий прочные фундаментальные знания и умеющий мыслить нестандартно и креативно.
  Август Мёбиус в молодые годы. Август Фердинанд Мёбиус родился 17 ноября 1790 в Шульпфорте, ныне Саксония. Начальное образование Мёбиус получил дома и сразу выказал интерес к математике. С 1803 по 1809 годы учился в гимназии-интернате Шульпфорта, затем поступил в Лейпцигский университет. Первые полгода, в соответствии с рекомендациями семьи, он изучал право, но затем принял окончательное решение посвятить жизнь математике и астрономии. С 1816 года он работал сначала астрономом-наблюдателем, затем директором в Плейсенбургской астрономической обсерватории (близ Лейпцига). Деятельно участвовал в перестройке и оснащении обсерватории. Мёбиус известен как автор большого количества первоклассных работ по геометрии, особенно проективной геометрии, анализу и теории чисел. В области астрономии Мёбиус опубликовал несколько значительных работ по небесной механике, о принципах астрономии и о планетных затмениях; среди них наибольшую известность получило сочинение «Элементы небесной механики» (1843). Стал знаменит как изобретатель листа Мёбиуса (ленты Мёбиуса) — простейшей неориентируемой двумерной поверхности. Согласно легенде открыть Мёбиусу свой «лист» помогла горничная, которая то ли неправильно сшила концы ленты, то ли неверно повязала шейный платок. В 1858 году профессор Лейпцигского университета, астроном и геометр Август Мёбиус послал в Парижскую Академию Наук научную работу, содержавшую сведения об этом необычном листе и его свойствах. Целых семь лет он дожидался её рассмотрения, а, не дождавшись, опубликовал в печати и стал знаменитым! Лента Мёбиуса сразу же привлекла внимание, как математиков, так и любителей всего занимательного. Однако, справедливости ради надо сказать, что эта фигура независимо от Мёбиуса в том же самом году была построена и другим немецкими математиком - Иоганном Листингом, который придумал математический термин «топология». Умер Август Фердинанд Мёбиус 26 сентября 1868 года в Лейпциге. В честь учёного назван астероид 28516.
Чем же интересен этот лист? А тем, что у листа Мёбиуса — всего одна сторона. Мы же привыкли к тому, что у всякой поверхности, с которой мы имеем дело, две стороны. Лента Мёбиуса обладает любопытными свойствами. Если попробовать разрезать ленту пополам по линии, равноудалённой от краёв, вместо двух лент Мёбиуса получится одна длинная двухстороння (вдвое больше закрученная, чем лента Мёбиуса) лента, которую фокусники называют "афганская лента". Если теперь эту ленту разрезать посередине, получатся две намотанные друг на друга . Другие интересные комбинации лент могут быть получены из лент Мёбиуса с двумя или более полуоборотами в них. Например, если разрезать ленту с тремя полуоборотами, то получится лента, завитая в узел трилистника. Разрез ленты Мёбиуса с дополнительными оборотами даёт неожиданные фигуры, названные парадромными кольцами. Чтобы сделать лист Мёбиуса надо взять достаточно вытянутую бумажную полоску и соединить концы полоски, предварительно перевернув один из них. Находясь на поверхности листа Мёбиуса, можно было бы идти по ней вечно. "Если кто-нибудь попробует раскрасить "только одну" сторону поверхности ленты Мёбиуса, пусть лучше сразу погрузит её всю в ведро с краской",— пишут Рихард Курант и Герберт Роббинс в превосходной книге "Что такое математика". Возьмём ленту, разделим каждую её сторону на три одинаковые полоски и склеим, перекрутив один раз лист. Будем резать по пунктирной линии. Если бы лента не была перекручена, то сначала мы бы отрезали одно кольцо, а потом ещё два остальных. Всего три кольца, каждое той длины, что и первоначальное, но второе меньшей ширины. Но у нас лист Мёбиуса. И, не отрывая ножниц от бумаги, разрежем пунктирными линиями сразу и получим два сцеплённых кольца. Одно из них вдвое длиннее исходного и перекручено два раза. Преподаватель: Бутылка Клейна - это своего рода лента Мебиуса в пространстве. Можно попасть внутрь бутылки не переходя через край. Это односторонняя поверхность, не имеющая края.
Бутылка Клейна – это мистический совершенный герметичный сосуд, где внешнее переходит во внутреннее и внутреннее во внешнее, который содержит сам себя и переходит сам в себя,у которого внутреннее и внешнее едино . Всё это чем-то напоминает змею, свернувшуюся в кольцо и заглатывающую свой собственный хвост . Впервые упоминание об этом объекте появилось в 1882 году, автором был немецкий математик Феликс Клейн, создатель нового направления в геометрии. 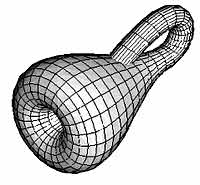 С точки зрения математики "бутылка Клейна" - это замкнутая (т.е. без края) односторонняя поверхность. Невозможно построить абсолютно правильную модель этого объекта в нашем трехмерном мире: здесь будет наблюдаться пересечение поверхности, что отсутствует в четырехмерном измерении. Вывод: истинная "бутылка Клейна" может существовать только в четырехмерном измерении! Допустим у нас есть бутылка с очень длинным горлом, в стенке и в донышке бутылки есть небольшие отверстия, соответствующие размеру горлышка. Берем бутылку за горло, изгибаем его, пропускаем вплотную через боковое отверстие, дотягиваемся горлышком до отверстия в дне бутылки и совмещаем их. У такой бутылки нет края, и ее поверхности нельзя разделить на внешнюю (наружную) и внутреннюю! Путешествие муравья по поверхности бутылки Клейна превратится в бесконечность! Ему не придется переходить с внешней стороны бутылки на внутреннюю - она единственная! И это будет справедливо и для теоретической, и для стеклянной "бутылки Клейна". Если рассечь бутылку вдоль вертикальной оси симметрии, то мы получим две ленты Мебиуса. Но, интересно, что с помощью одного замкнутого разреза бутылку Клейна можно превратить даже всего лишь в один лист Мебиуса! Есть сувенирные бутылки Клейна в виде графина для вина, только вот пользоваться ими достаточно трудно. Их трудно наполнять, т.к. жидкость создает дополнительное давление на воздух внутри, а ему некуда деваться ... С выливанием жидкости тоже много проблем. Но "плюс" - это то, что жидкость в бутылке Клейна не испаряется. Однако, стенки изнутри практически невозможно очистить. Преподаватель: Открытие Мебиуса послужило толчком к развитию новой науки – топологии. Топология это раздел математики, занимающийся изучением свойств фигур (или пространств), которые сохраняются при непрерывных деформациях, таких, например, как растяжение, сжатие или изгибание.) В популярной литературе топологию часто называют «геометрией на резиновом листе», поскольку ее наглядно можно представлять себе как геометрию фигур, нарисованных на идеально упругих резиновых листах, которые подвергаются растяжению, сжатию или изгибанию. Топология - один из новейших разделов математики. Вернемся к листу Мебиуса. На первый взгляд может показаться, что этот объект годится только для фокусов и развлечений. Но существует огромное количество технических применений ленты Мебиуса.
Удивительные свойства ленты Мёбиуса используются в самых различных изобретениях. Полоса ленточного конвейера выполняется в виде ленты Мёбиуса, что позволяет ему работать дольше, потому, что вся поверхность ленты изнашивается равномерно. На наружную сторону ленты нанесён шлифовальный порошок. Ленту прижимают к изделию, прокручивают, идёт шлифовка. Через какое-то время стирается и сам шлифовальный слой на ленте. Приходится прерывать процесс, менять ленту. Как сделать, чтобы лента работала вдвое дольше, если размеры ленты увеличивать нельзя? В 1969 году изобретателю А. Губайдуллину было выдано авторское свидетельство на шлифовальное устройство с лентой Мёбиуса: срок работы ленты увеличились вдвое. В технике так же применяется резистор Мебиуса, прокатный стан, ремень передачи, подшипник в виде ленты Мебиуса для увеличения срока   Благодаря ленте Мёбиуса, были созданы особые кассеты для магнитофона, которые дали возможность слушать магнитофонные кассеты с “двух сторон” не меняя их местами. В большинстве матричных принтеров красящее устройство также имеет вид листа Мёбиуса для увеличения его ресурса. В 1971 году изобретатель с Урала Чесноков П.Н. применил фильтр в виде листа Мёбиуса. И это только малая часть примеров использования этой удивительной поверхности. Преподаватель: Лист Мебиуса похож на знак бесконечности и внешне и по своим свойствам с точки зрения философии.
Нынешний символ бесконечности "∞" ввел в употребление Джон Уоллис в 1655 году. Джон Уоллис издал большой трактат «Арифметика бесконечного»), где ввёл придуманный им символ бесконечности. До сих пор так и не известно, почему он остановил свой выбор именно на этом знаке. Одна из наиболее авторитетных гипотез связывает происхождение этого символа с латинской буквой «М», которую римляне использовали для обозначения числа 1000. Символ бесконечности назван "lemniscus" (лат. лента) математиком Бернулли приблизительно сорок лет спустя. Другая версия говорит о том, что рисунок «восьмерки» передает главное свойство понятия «бесконечность»: движение без конца. По линиям числа 8 можно совершать бесконечное движение. Для того, чтобы не путать введенный знак с числом 8, математики решили располагать его горизонтально. Такое обозначение cтало стандартным для всей математики, не только алгебры. Почему бесконечность не обозначают нулем? Ответ очевиден: цифру 0 как не поворачивай — она не изменится. Поэтому выбор и пал именно на 8. Д  ругой вариант – уроборос - змей, пожирающий свой хвост, который за полторы тысячи лет до нашей эры в Египте символизировал различные процессы, не имеющие начала и конца. Бесконечность — вообще одно из самых удивительных понятий науки, понятие, которое, пожалуй, больше чем какое-либо другое с давних пор привлекает к себе внимание. Может быть, это объясняется тем, что в повседневной жизни нам всегда приходится иметь дело только с конечными величинами, с конечным числом тех или иных объектов, а бесконечность манит человека своей необычностью и даже таинственностью. С понятием бесконечности мы сталкиваемся, говоря о Вселенной. Еще великие философы древности пытались решить вопрос о бесконечности Вселенной в пространстве с помощью сравнительно простых и, казалось бы на первый взгляд, неопровержимых логических рассуждений. Представим себе, — говорили они, — что у Вселенной есть край и человек достиг этого края. Однако стоит ему только вытянуть руку, и она окажется за границами Вселенной. Но тем самым рамки мира раздвигаются еще на некоторое расстояние. Тогда можно будет приблизиться к новой границе и повторить ту же операцию еще раз. И так без конца. Значит, Вселенная не может иметь границ. «Нет никакого конца ни с одной стороны у Вселенной, ибо иначе края непременно она бы имела», — писал Лукреций Кар в своей поэме «О природе вещей».  На протяжении многих веков ученые астрономы обсуждают вопрос строения и бесконечности Вселенной. Одна из новейших гипотез говорит о том, что Вселенная имеет форму листа Мебиуса, т.е. она бесконечна, но при этом ограничена. Кроме того, космический инфракрасный телескоп Herschel обнаружил в центре нашей Галактики перекрученное кольцо плотного газа, напоминающее по форме символ бесконечности или лист Мебиуса. До сих пор астрономам удавалось увидеть только часть этого кольца, протянувшегося на расстояние 600 световых лет.  Если отмечать положение Солнца на небе каждый день в одно и то же время в течение земного года, то мы получим аналемму, кривую, в виде знака бесконечности или листа Мебиуса. Подобные наблюдения были сделаны еще в каменном веке, что отражено в так называемых «каменных кораблях», найденных на территории Швеции, Норвегии, Финляндии, Германии, Прибалтики и России. Все они были построены 1,5 – 2,5 тысячи лет назад по Во время летнего и зимнего солнцестояния светило восходит и заходит здесь в определенных точках и, вероятно, древние скандинавы возвели астрономическую обсерваторию, которая служила для ежегодных религиозных церемоний или для обслуживания сельскохозяйственного цикла.  Запредельная звёздная вечность… Нам её никогда не постигнуть. Это сложно понять – бесконечность: Будто в воду холодную прыгнуть. Бесконечность – вопрос без ответа На холодных губах тонкой льдинкой, Незабвенные строки поэта, На которых застыла слезинка. Наша память, хранящая файлы Жизни прошлой и жизни грядущей. Бесконечность – она не случайна, Как и всё в этом мире насущном. Преподаватель: Нам знакомо понятие бесконечности в математике. Но, проблема в том, что мы не умеем выполнять действия над бесконечно большими и бесконечно малыми величинами. Выражения вида  называют неопределенностью. Проблемы бесконечности, которую нельзя ни постичь, ни измерить, давно интересовали нижегородского ученого Ярослава Сергеева. Несколько лет назад он ввел единицу измерения бесконечности, создав таким образом новый математический язык.  Ярослав Сергеев стал первым российским ученым и пятым ученым в мире, удостоенным премии Пифагора. 47-летний профессор Нижегородского государственного и Калабрийского университетов получил награду за работы, которые позволили ученым более эффективно оперировать бесконечно малыми и бесконечно большими числами. Идея профессора Сергеева заключалась в том, что проблемы работы с бесконечностью происходят из-за несовершенства существующего математического языка, и он разработал новый язык, который позволяет не только записывать бесконечно малые и большие числа, но и производить с ними обычные математические действия. Сергеев уже разработал и запатентовал в России, Европе и США новый "компьютер бесконечности", который способен выполнять вычисления с бесконечно большими и малыми числами. Мои исследования носили фундаментальный характер, но они найдут и широкое прикладное применение везде, где только есть математика, - сказал профессор Сергеев "Известиям". - У нас уже есть первый калькулятор, с помощью которого мы производим более точные вычисления. Преподаватель: Вернемся снова к листу Мебиуса. Его необыкновенные свойства вдохновляли художников, архитекторов и скульпторов на создание необычных произведений искусства.
Лист Мёбиуса служил вдохновением для скульпторов и для графического искусства. Известный голландский художник М. Эшер (1898-1971) особенно любил его и посвятил несколько своих литографий этому математическому объекту. Одна из известных — лист Мёбиуса, показывает муравьёв, ползающих по поверхности ленты Мёбиуса. 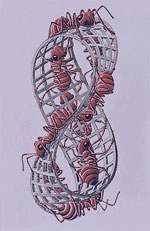  У входа в Музей истории и техники в Вашингтоне медленно вращается на пьедестале стальная лента, закрученная на полвитка  Целую серию скульптур в виде листа Мебиуса создал скульптор Макс Билл.Г  игантская скульптура «Древо жизни» сочетает в себе мотивы древесной коры, человеческого сердца и «Листа Мёбиуса», символизирующие творческий союз искусства и науки.Небольшие скульптуры с изображением листа Мёбиуса являются украшением парков и скверов. Минск. Скверик около Центральной Научной библиотеки имени Якуба Коласа. 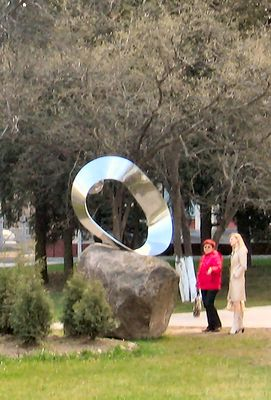 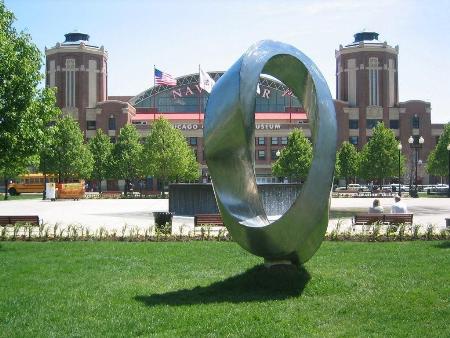 Это украшение в виде ленты Мебиуса выполнено в Риге в 2001 г   Скульптура в Москве.Преподаватель: Сегодня мы познакомились с необыкновенным объектом, который на первый взгляд, не имеет ничего общего с математикой. Но это лишний раз подтверждает, что математика универсальная наука, охватывающая все сферы жизни человека и человечества. Хочется думать, что сегодняшняя конференция многих заставит взглянуть на математику по-другому, вызовет интерес к занятиям наукой. |
Опыты с листом Мебиуса.