«Квадратные уравнения»

Скачать 66.38 Kb. Название «Квадратные уравнения» Дата 05.04.2016 Размер 66.38 Kb. Тип План-конспект

План-конспект урока «Квадратное уравнение и его корни» (урок по алгебре для 8 класса по базовой программе) Учебник: Алгебра8 под ред. Ш.А.Алимова Подготовила: Панина Елена Викторовна учитель математики ГБОУ гимназии №528 Санкт-Петербурга Тема: «Квадратные уравнения» 1 урок в данной теме Тип урока: -урок изучения и первичного закрепления новых знаний. Цели урока: формирование понятия квадратного уравнения и его видов по значениям коэффициентов; Задачи: Образовательные: сформулировать определение квадратного уравнения; -рассмотреть структуру и определить компоненты; - рассмотреть различные виды кв.уравнений; -сформулировать и научить применять теорему о корнях уравнения х² = d. Развивающие: Способствовать развитию умственных способностей ребенка путем формирования логической культуры и, аналитических способностей Воспитательные: - продолжить работу по формированию ответственности учащихся за свою деятельность на уроке, умений самостоятельно думать, проводить сравнительный анализ, развивать речь учащихся, овладению способами и критериями самоконтроля и самооценки. В результате ученик знает - определение квадратного уравнения, - название коэффициентов квадратного уравнения, -определение полного и неполного квадратного уравнения - теорему о корнях уравнения х² = d.; Умеет - из предложенных уравнений выбирать квадратные, определят их коэффициенты; - классифицировать квадратные уравнения по значениям коэффициентов и приводить их к стандартному виду; - составлять квадратное уравнение, если заданы коэффициенты; -решать простейшие уравнения вида х²=.d.- Понимает - какие учебные задачи стоят перед ним при изучении темы «Квадратные уравнения» -принцип решения квадратного уравнения и может прогнозировать результат своей работы. Оборудование Компьютер учителя, интерактивная доска Учебник алгебра 8 Презентация Рабочие тетради учеников. Структура урока: I. Мотивационно – ориентировочная часть: - актуализация знаний - мотивация, постановка учебной задачи. II. Операционно – познавательная часть: - решение учебной задачи (сообщение нового материала, первичная проверка понимания учащимися нового материала, закрепление изученного материала). III. Рефлексивно – оценочная часть: - подведение итогов урока, - комментарий к выполнению домашнего задания. Формы работы учащихся: коллективная, индивидуальная План урока: № Этап урока Содержание (цель) этапа Время мин. Организационный момент Формирование мотива, желания работать на уроке. 1 Проверка домашней работы 1 Устная работа Повторение необходимых теоретических сведений, применение наработанных умений и навыков в изученном материале (рассматриваемом в новой теме), развитие умений говорить и слушать. 10 Введение новых понятий и первичная отработка полученных знаний Ввести понятие квадратного уравнения и сводящегося к нему, научить определять коэффициенты, научить записывать квадратное уравнение по заданным значениям коэффициентов, ввести понятие полного и неполного квадратного уравнения, научить решать уравнения вида х² = d 30 Итог урока Обобщить результаты работы за урок, выставить оценки, прокомментировать домашнее задание 3 Ход урока: Организационный момент Здравствуйте, садитесь. Приготовьте все необходимое к уроку: учебник, тетрадь, дневник. Сегодня…..число. Тема сегодняшнего урока «Квадратное уравнение и его корни» Сегодня мы начинаем изучать новую, очень важную тему из курса алгебры. Одну из основных. Будьте внимательны и не стесняйтесь задавать вопросы, если вам что-то непонятно. Проверка домашнего задания (если оно задавалось по предыдущей теме) Актуализация имеющихся знаний и умений учащихся Для того, чтобы изучение новой темы было достаточно последовательным, нам необходимо с вами повторить некоторые темы, которые участвуют в формировании новых понятий. Устная работа: Введение новых понятий и первичная отработка полученных знаний Я прошу вас подготовить в тетради 4 столбика. В ходе самостоятельной работы ученики пробуют самостоятельно классифицировать уравнения по степени неизвестного. В рабочей тетради записать номера уравнений в четыре столбика. 1 группа – равенства, не содержащие неизвестного Вывод: - все остальные равенства это уравнения. Повторить определение уравнения. 2 группа – линейные уравнения - Каков общий вид линейного уравнения? (ах + с = 0) - Как называются числа а и с, какие значения они могут принимать? ( Это коэффициенты уравнения, они могут быть любыми, кроме случая, когда а = 0) 3 группа- уравнения, в которых переменная возведена во вторую степень 4 группа- уравнения, в которых переменная возведена в более высокую степень. На сегодняшнем уроке мы с вами подробно изучим уравнения вида, представленного в третьей группе. Отметить хорошо видимый признак такого рода уравнений – переменная во второй степени. Ввести определение квадратного уравнения, квадратного трехчлена, стандартного вида квадратного уравнения, название коэффициентов. Квадратным уравнением называется уравнение вида ах2 + bх + с = 0, где а, b, с – заданные числа, а ≠ 0. Числа a, b,c – это коэффициенты квадратного уравнения. Число а называют первым или старшим коэффициентом, b - вторым коэффициентом, а c-свободным членом. Работа с учебником: №401, 402 (устно) Далее работа со слайдом: -Всегда ли возможно определить коэффициенты квадратного уравнения по его записи? -Какое из предложенных уравнений записано в стандартном виде? -Какие уравнения необходимо преобразовать, для того, чтобы привести к стандартному виду и как это сделать? Определить значения коэффициентов в полученных уравнениях. Работа на доске и в тетрадях с проверкой результата по слайду. Так же мы должны научиться не только уметь считывать значения коэффициентов, но и записывать квадратные уравнения с заданными значениями коэффициентов. Записать на доске полученные уравнения. Во время работы мы с вами выяснили, что коэффициенты b и с могут быть равными нулю. Попробуем изучить вид квадратного уравнения в таких случаях. Приведем примеры таких уравнений (записать на доске). 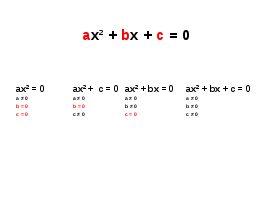Вернуться к уравнениям на доске, еще раз проговорить коэффициенты каждого уравнения. Для чего нам необходима такая классификация? Для того, чтобы научиться решать такого вида уравнения. Существует несколько способов решения таких уравнений. Но для этого мы должны четко понимать, что значит решить уравнение и каков должен быть результат нашей работы. - Дайте определение корня уравнения. (Корень уравнения – это такое число, при подстановке которого в уравнение получается верное числовое равенство) - А что значит решить уравнение? ( Решить уравнение – найти все его корни или установить, что их нет) Как проверить, является ли число корнем уравнения? Работа по учебнику №405(1,3-устно, 5 письменно на доске) Рассмотрим способы решения квадратных уравнений. Первая группа уравнений: №408,409 найдите уравнения такого типа. Очевидно, сто такие уравнения имеют корень 1. 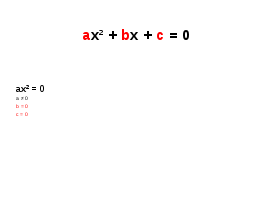Рассмотрим уравнения второго типа. В номере 408 (1) Записать на доске и решить через разность квадратов. Два корня. Арифметический корень и противоположное арифметическому корню число. Ввести формулу (теорему) 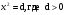Вполне понятно, что эти два случая можно объединить как уравнение вида 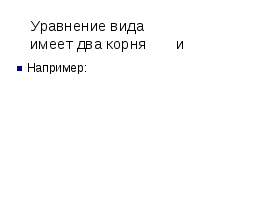По учебнику решить устно №407, №408(3,5) Подвести итоги урока .Работа со слайдом. Домашнее задание: п.25 стр.108 определение кв. уравнения, определение полного и неполного кв. уравнения, теорема о корнях №403, 404,408(чет)409чет Спасибо за урок. До свидания!