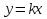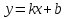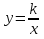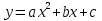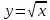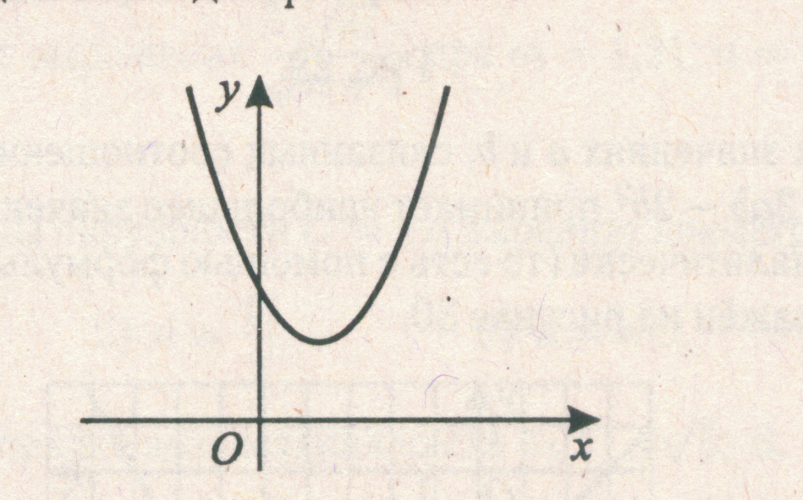«Квадратичная функция и ее график»

Название	«Квадратичная функция и ее график»
Дата	05.03.2016
Размер	58.7 Kb.
Тип	Документы

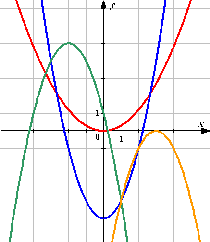
Тема: «Квадратичная функция и ее график»

ХОД УРОКА

I Организационный момент

Вводная беседа учителя.

Французский писатель Анатоль Франс (1844-1924) однажды заметил: «Учиться можно только весело…Чтобы переваривать знания, надо поглощать их с аппетитом».

Давайте на уроке будем следовать этому совету писателя, будем поглощать знания с большим желанием, ведь они пригодятся вам всегда. Будьте активны и внимательны.

Сегодня у нас урок - семинар по теме «Квадратичная функция и ее график». Повторяем, обобщаем, приводим в систему изученный материал по данной теме. Ваша задача: показать свои знания, умения и навыки по данной теме при решении задач, при необходимости совершенствовать имеющиеся знания.

II Устная работа

(слайд 4)

Вопросы:

1) Функция – это одно из важнейших математических понятий. А что же такое функция?

2) Какую переменную называют независимой переменной?

3) А какую – зависимой переменной?

4) Назовите формулу, которой задается квадратичная функция.

5) Как называется график квадратичной функции.

6) Назовите область определения и множество значений квадратичной функции.

№1

Какие из этих графиков не являются графиками функций?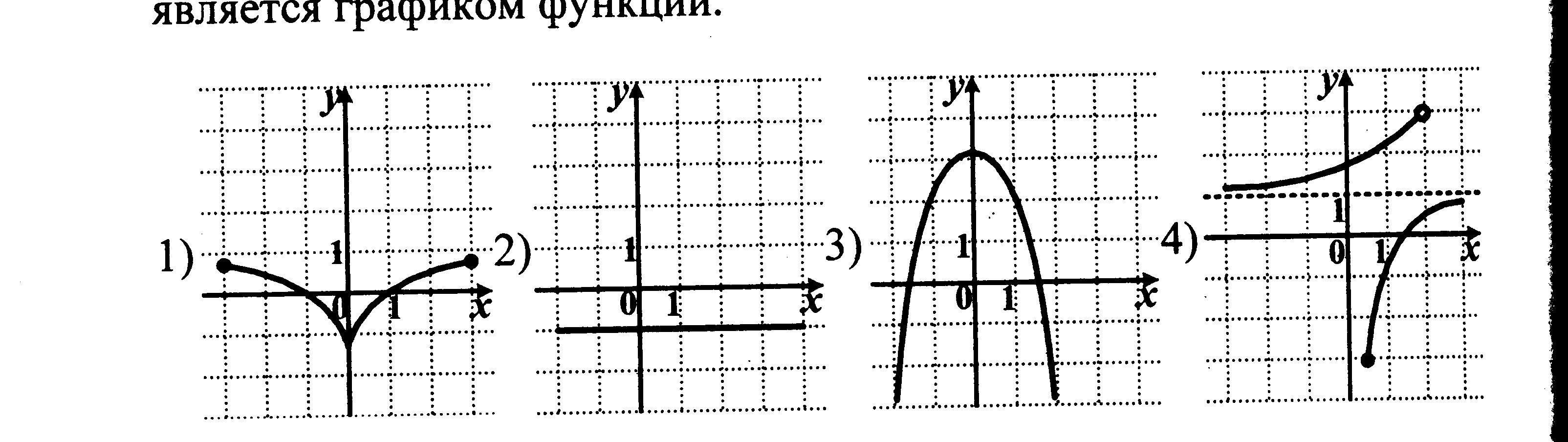

$c:\documents and settings\администратор\рабочий стол\новая папка\image1.bmp$ Ответ: 4

№2

Найдите соответствия

$c:\documents and settings\администратор\рабочий стол\функция разноуровневый урок\для презентации\рисунок1.wmf$
	у = х²– 5
	у = 0,3х²
	у = – (х – 3)²
	у = – (х+ 2)² +5

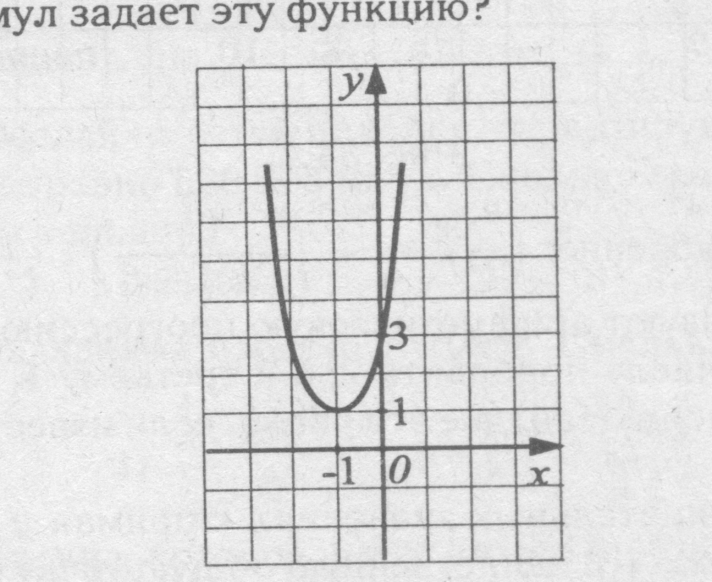
Ответ: 1 – синий, 2 – красный, 3 – жёлтый, 4 – зеленый

№3

На рисунке изображен график квадратичной функции. Какая из перечисленных формул задает эту функцию?

$c:\documents and settings\администратор\мои документы\my pictures\scan pictures\20100511\image3.bmp$	у = – 2х² +4х – 3
	у = – 5х² +10х + 3
	у = х² +2х + 3
	у = 2х² +4х + 3

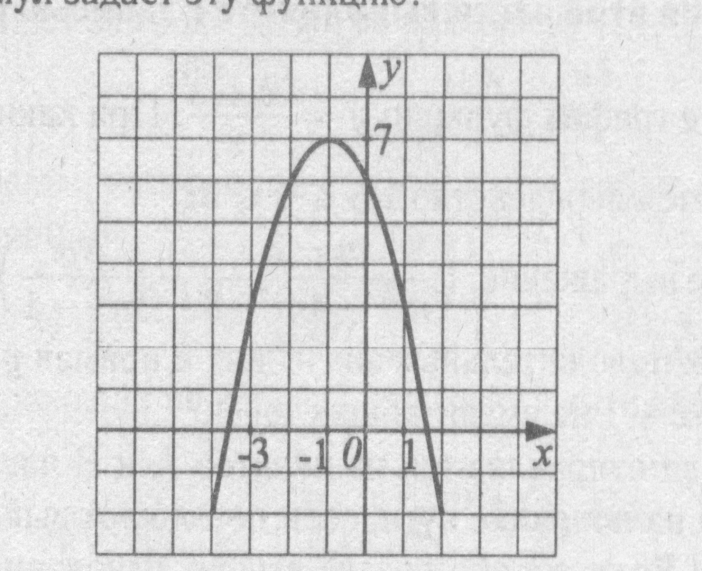
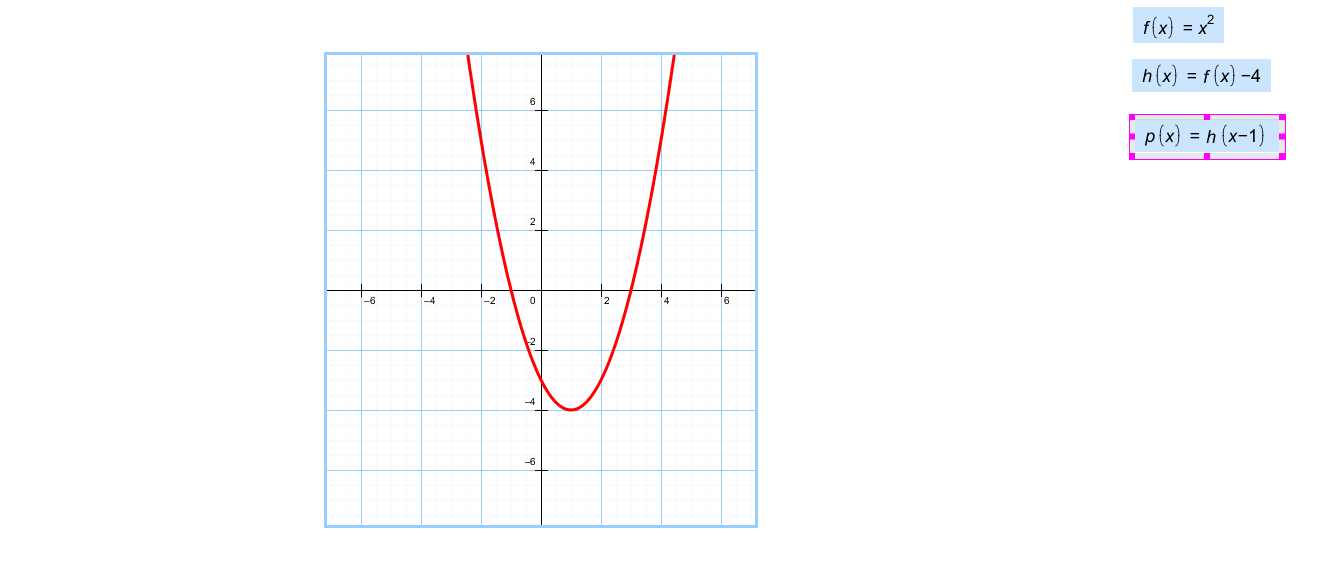
Ответ: 4

№4

На рисунке изображен график квадратичной функции. Какая из перечисленных формул задает эту функцию?

$c:\documents and settings\администратор\мои документы\my pictures\scan pictures\20100511\image4.bmp$	у = – х² –2х + 6
	у = – х² +2х + 6
	у = – х² –2х + 8
	у = – х² +2х +8

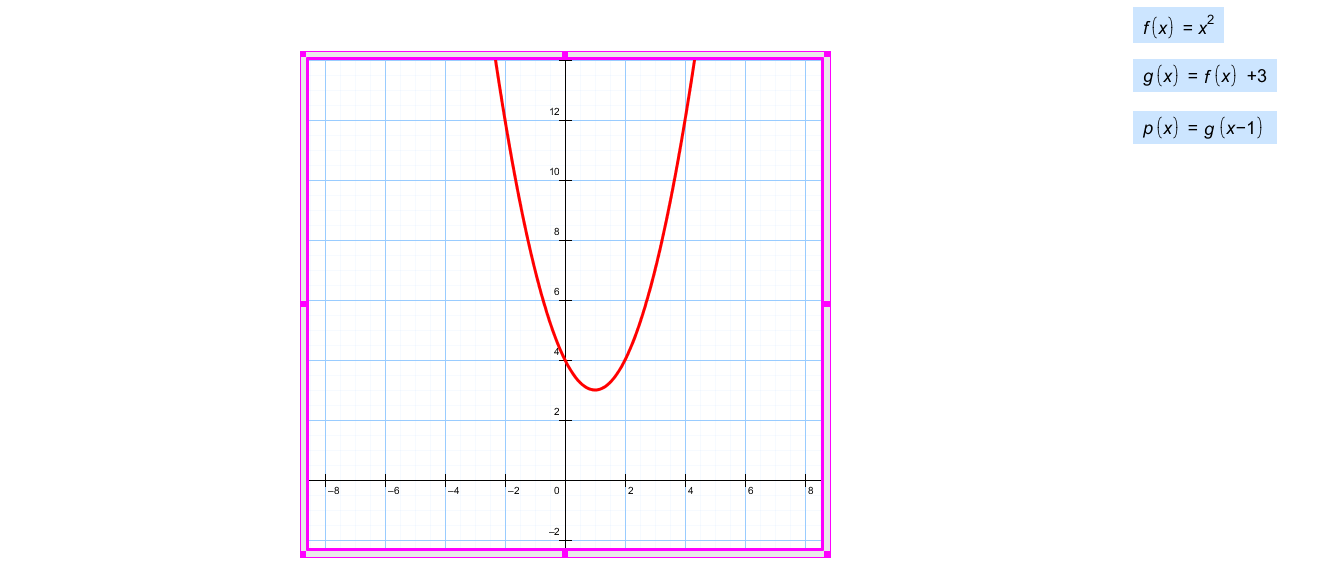
Ответ:1

Что можете сказать о дискриминанте? (D>0)

№5

На рисунке изображён график функции у = ах² +bх + c. Определите знаки коэффициента а и дискриминанта D.

$c:\documents and settings\администратор\мои документы\my pictures\scan pictures\20100511\image5.bmp$	a > 0, D > 0
	a > 0, D < 0
	a < 0, D > 0
	a < 0, D < 0

Ответ: 2

№6

Установите соответствие между графиками функций и формулами, которые их задают.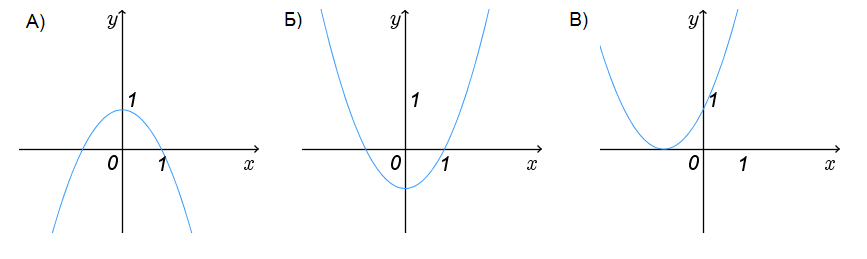

https://ege.yandex.ru/media/gia-2013/math/v10/mayh-gia_v10_5.png

y=x²+1
y=(x+1)²
y=1−x²
y=x²−1

А 3 Б 4 В 2

III Решение разноуровневых заданий (с проверкой)

Учитель. Открыли тетради, записали дату и тему урока.

К доске вызываются три ученика, которые работают по карточкам. Задания для карточек разной сложности. Остальные учащиеся работают в своих тетрадях самостоятельно, выполняя задание своей группы. Затем сверяют решение с теми учениками, которые работали у доски.

На рабочем месте обучающегося лежат три карточки. Ученик выбирает себе сам уровень сложности.

Карточка №1 (оценка «3»)

1) С помощью шаблона у=х² построить график функции у = х²+2;

2) Укажите координаты вершины параболы у = х² +4х+ 1.

Решение.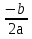

х₀ =

; х₀ =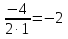

; у₀ = ( – 2)² +4·(– 2) +1 = 4 – 8+1 = – 3.

Ответ: (– 2; – 3).

Карточка №2 (оценка «4»)

1) С помощью шаблона у=х² построить график функции у = – (х–2)²

2) Найдите координаты точек пересечения параболы у = х² –3х + 2 с осями координат.

Решение.

Парабола пересекает ось ОУ (х = 0). Если х = 0, то у = 2.

Парабола пересекает ось ОХ (у = 0). Если у = 0, то х² –3х + 2 = 0; х₁ =1; х₂ =2.

Ответ: (0;2); (1;0); (2;0).

Карточка №3 (оценка «5»)

1) С помощью шаблона у=х² построить график функции у = – (х + 2)² – 3;

2) Найдите наименьшее значение функции у = 2х² +4х – 3 при х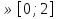

.

Решение.

Графиком функции является парабола, ветви которой направлены вверх. Вершина параболы находится в точке (– 1; –5). На интервале [– 1; +∞) данная функция возрастает. Значит, и на отрезке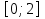

функция тоже возрастает. Наименьшее значение эта функция примет при наименьшем значении х, т.е. при х = 0. Если х = 0, то у = – 3.

Ответ: – 3.

IV Проверочная работа (карточки)

Приложение (карточки)

Вариант	1	2	3
А1	4	3	4
А2	2	1	2
А3	3	4	3
В1	-1;0,25	-0,5;1	-3;0,5
С1

V Итог урока

Учитель подводит итог урока, оценивает работу учеников и ориентирует в домашнем задании.

VI Домашнее задание

1 группа	Дидактический материал для 9 класса по алгебре	С-8, № 1, 2,3
2 группа	Дидактический материал для 9 класса по алгебре	С-8, № 2,3,4
3 группа	Дидактический материал для 9 класса по алгебре	С-8, № 2,3,4,5

Для домашней работы предлагаю задания аналогичные тем, что мы делали в классе.

VII Историческая справка

И последний вопрос: Кто из ученых впервые ввёл термин «функция»?

(показать слайд и дать историческую справку о Лейбнице).

VII Рефлексия

– Сегодня каждый из нас закончил работу с определенным настроением. Какое оно у вас я не знаю, а могу лишь догадываться.
Для того чтобы передать эмоциональное настроение, при работе на компьютере используют смайлики (от англ. smile – улыбка). Оцените свою работу на уроке, используя смайлики. (У детей на столах лежат смайлики).

Учитель предлагает детям прикрепить смайлики в зависимости от того, как они оценивают свой успех на уроке:

: – ) – те, кто считает, что хорошо поработал на уроке.
: – ? – те, кто считает, что недостаточно хорошо поработал на уроке.
: – ( – те, кто считает, что ему еще нужно работать над данной темой.

Спасибо за работу добросовестную и ответственную, спасибо за труд и умение,

такт и общение.