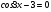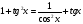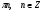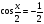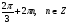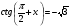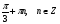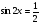Конспект урока по математике в 10 классе «Различные способы решения тригонометрических уравнений»
 Скачать 156.94 Kb. Скачать 156.94 Kb.
|
| Муниципальное бюджетное общеобразовательное учреждение Бутурлиновская средняя общеобразовательная школа Бутурлиновского муниципального района Воронежской области Конспект урока по математике в 10 классе «Различные способы решения тригонометрических уравнений». Подготовила учитель математики Коротких Эмма Александровна 2015 год Цели урока: Образовательные: - систематизация знаний учащихся по теме «Методы решения тригонометрических уравнений»; -углубление знаний по теме; - формирование умения классифицировать тригонометрические уравнения по методам решений, применять эти методы в новой ситуации. Развивающие: – способствовать развитию аналитико-синтетического мышления, внимания; - содействовать развитию логического, математического мышления учащихся. Воспитательные: - развивать у учащихся коммуникативные способности, элементы ораторского искусства; - способствовать развитию творческой деятельности учащихся, потребности к самообразованию. Оборудование: экран, проектор, карточки для самостоятельной работы, карточки с проверочной работой «Карусель», интерактивная доска, система опроса и тестирования PrometheanActivExpression, таблицы: «Тригонометрический круг», «Тригонометрия», «Тригонометрические уравнения», индивидуальный справочный материал,индивидуальные оценочные листы; Мордкович А.Г. Алгебра и начала математического анализа. 10-11 классы. В 2 ч. Ч. 1.Учебник (задачник) для учащихся общеобразовательных учреждений (базовый уровень), - М.: Мнемозина, 2012. Тип урока: урок обобщения и систематизации знаний Методы обучения:метод постановки проблемы и метод поиска решений. Формы организации урока: индивидуальная, фронтальная, групповая. Педагогические приемы урока:эпиграф, наблюдение, обобщение, общественный смотр знаний, самостоятельная и проверочная работы. План урока:
1.Самостоятельная работа: блиц-опрос - контроль знаний по простейшим тригонометрическим уравнениям (система опроса и тестирования Promethean ActivExpression,системное голосование) (8 мин). 2.Повторение: методы решения тригонометрических уравнений (13 мин).
Конспект урока
Учитель - Сегодня на уроке мы будем учитьсяприменять различные методыв решении тригонометрических уравнений, которые занимают важное место в математическом анализе. Математика способствует развитию умений анализировать, сопоставлять, творчески мыслить. Правильное решение по-своему красиво, а поиск решения всегда интересен. Эпиграфом нашего урока будут словаМ. И. Калинина:  «Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе». II. Систематизация теоретического материала Учитель. - Посмотрите на уравнения (слайд). Каким способом их можно решить? (постановка проблемы). Пример 1 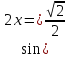 Пример 2 cos(x/5)=1 Пример 3. 1 + 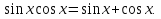 Пример 4 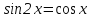 Пример 5. Решите уравнение 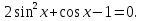 2sin2(x)+3cos(x)=0 Пример 6. 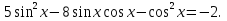 Пример7.2sin2(x)+3cos(x)=0 Пример 8. 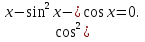 Учащиеся дают разные ответы. Учитель - Сравните и сопоставьте эти уравнения. Разбейте их на группы. Какими способами можно решить каждую получившуюся группу уравнений? Учащиеся - Решение простейших уравнений: примеры 1,2 - Метод разложения на множители:примеры 3, 4. - Метод замены переменных: примеры 5 ,6. - Решение уравнений с помощью применения тригонометрических формул:примеры 7, 8 Учитель Верно. Все тригонометрические уравнения, как правило, сводятся к простейшим уравнениям, которые мы научились решать с помощью общих формул простейших тригонометрических уравнений, их частных случаев, а также с помощью тригонометрических формул. Обратите внимание на таблицы и справочный материал: 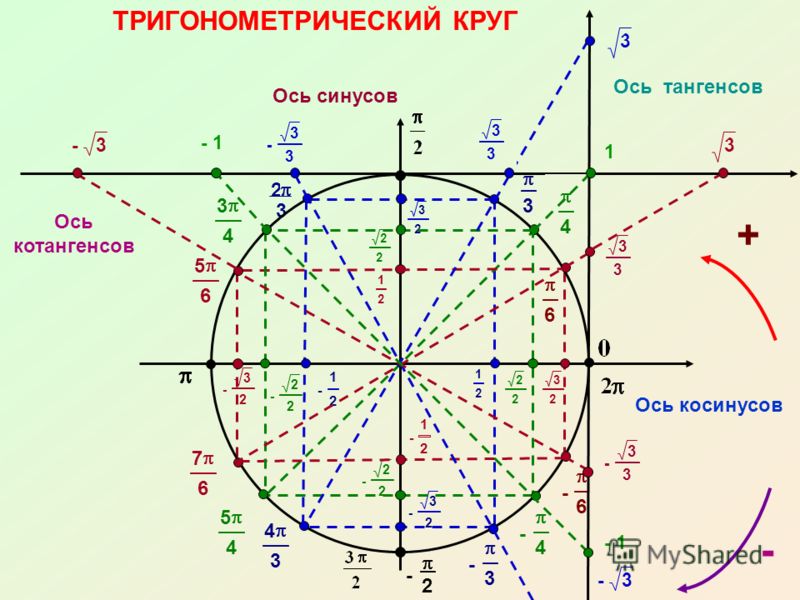 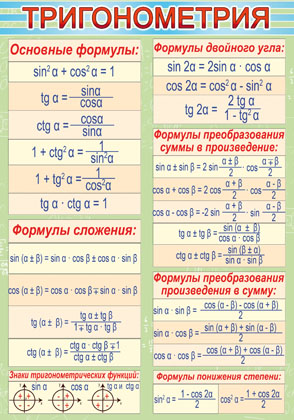 Справочный материал (на рабочем столе учащихся). Тригонометрические формулы. 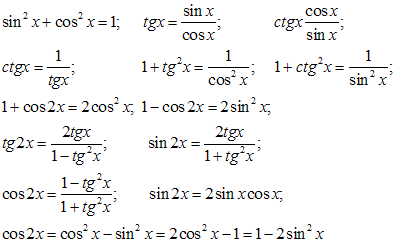 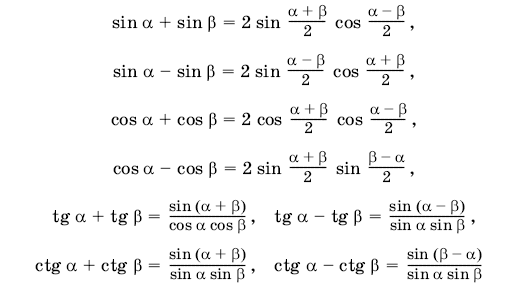 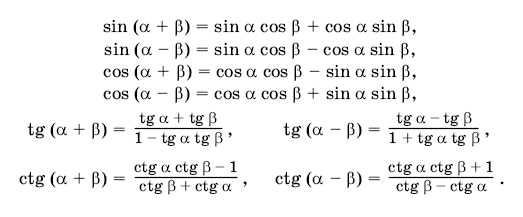 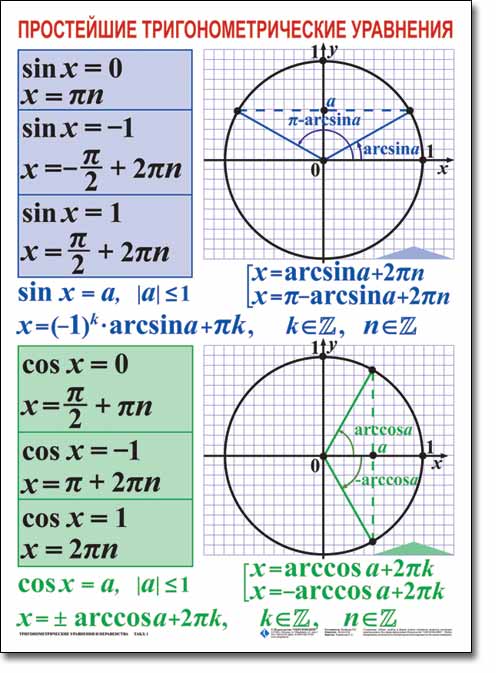 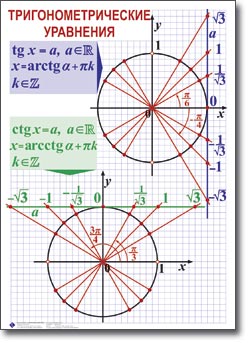 Справочный материал (на рабочем столе учащихся). Тригонометрические уравнения. С 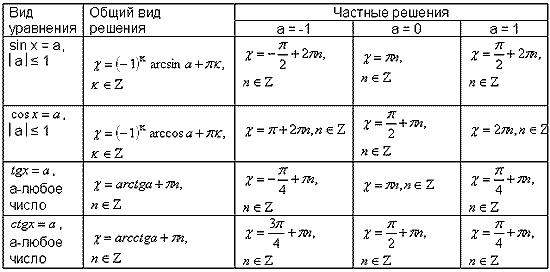 Учитель: Проверим ваши умения по решению простейших тригонометрических уравнений. 1. Самостоятельная работа. Блиц-опрос (проверка - системное голосование) За правильное решение учащиеся получают балл (самопроверка с последующей записью баллов в оценочный лист) Оценочный лист
2. Повторение. Учитель: - А сейчас вам предстоит работа в группах. Вы должны представить решение тригонометрического уравнения указанным методомв карточкеи составить алгоритм решения Учащиеся делятся на группы разной подготовленности. Обсуждают коллективно решение примеров. Учитель: Проверка задания: один человек группы произносит алгоритм решения тригонометрического уравнения, сверяясь с решением, предоставленным на слайде(используется материалы курса «Уравнения и неравенства в школьном курсе математики», П.В. Чулков, лекция №5, - М.: Педагогический университет «Первое сентября», 2010) Слайды 1 группа. Решение простейших уравнений. Пример 2(слайд) Решить уравнение: cos(x/5)=1 Решение: x/5= ± arccos(1) + 2πk. x/5=πk x=5πk Ответ:5πk, 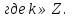 2 группа. Метод разложения на множители. Пример 3 (слайд). Решите уравнение 1 + 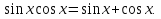 Решение. Перепишем уравнение в виде: 1 + 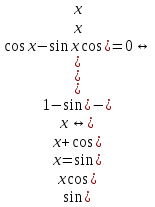 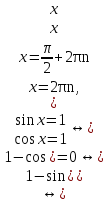 Ответ: 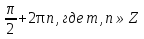 3 группа. Метод замены переменных. Пример 5 (слайд). Решите уравнение 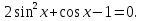 Решение. Запишем уравнение в виде 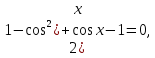 откуда откуда 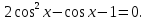 Заметим, что данное уравнение представляет собой квадратное уравнение относительно 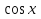 . Обозначим . Обозначим 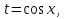 получим уравнение получим уравнение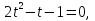 корни которого корни которого 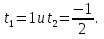 Получаем два случая: 1) 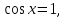 откуда откуда 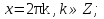 2) 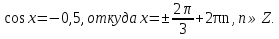 Ответ: 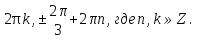 Учитель. Методом замены можно решать «однородные тригонометрические» уравнения. Тригонометрическое уравнение называют однородным, если после некоторой замены полученный многочлен от двух переменных составлен из одночленов одинаковой степени. Например: Слайд Решите уравнение 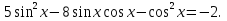 Решение. Перепишем уравнение в виде 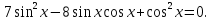 Получили уравнение, однородное относительно 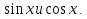 Рассмотрим два случая: 1) 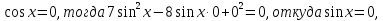 что невозможно, поскольку что невозможно, поскольку 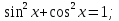 в этом случае корней нет. в этом случае корней нет.2) 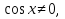 тогда разделим обе части уравнения на тогда разделим обе части уравнения на 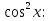 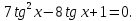 Пусть y = tgx. Получим: 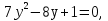 откуда откуда 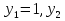 = = 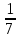 . .Осталось решить уравнения tgx = 1 и tgx = 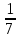 . .Ответ: 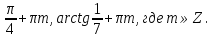 4группа. Решение уравнений с помощью применения тригонометрических формул. Примеры 7 (слайд). Решить уравнение: 2sin2(x)+3cos(x)=0 Решение: Воспользуемся тождеством: sin2(x)+cos2(x)=1 Наше уравнение примет вид: 2-2cos2(x)+3cos(x)=0 2cos2(x)- 3 cos(x) -2 = 0 введем замену t=cos(x): 2t2 -3t - 2 = 0 Решением нашего квадратного уравнения являются корни: t=2 и t=-1/2 Тогда cos(x)=2 и cos(x)=-1/2. Т.к. косинус не может принимать значения больше единицы, то cos(x)=2 не имеет корней. Для cos(x)=-1/2: x= ± arccos(-1/2) + 2πk; x= ±2π/3 + 2πk Ответ: x= ±2π/3 + 2πk Учитель: - При решении тригонометрических уравнений можно использовать универсальную тригонометрическую подстановку на основе Формул(слайд): 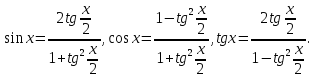 Если 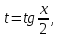 то то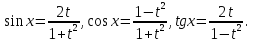 С помощью универсальной подставки мы можем любое уравнение вида 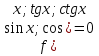 свести к алгебраическому уравнению. Важно при этом помнить, что, делая замену, мы можем потерять те корни исходного уравнения, для которых свести к алгебраическому уравнению. Важно при этом помнить, что, делая замену, мы можем потерять те корни исходного уравнения, для которых 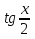 не определен, то есть значения не определен, то есть значения 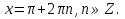 Их мы должны проверять отдельно. Их мы должны проверять отдельно.В следующем примере 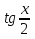 встречается изначально, поэтому универсальная подстановка не может привести к потере корней указанного вида. встречается изначально, поэтому универсальная подстановка не может привести к потере корней указанного вида.Слайд Решим уравнение 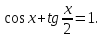 Решение (учащиеся записывают в тетради) Сделаем универсальную подстановку 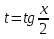 , тогда , тогда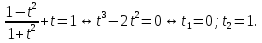 Таким образом: а) 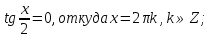 б) 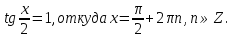 Ответ: 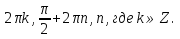 Учитель. В заданиях ЕГЭ встречаются тригонометрические уравнения, решаемые способом отбора корней. Рассмотрим решение такого уравнения (слайд): Найдите корни уравнения 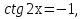 принадлежащие промежутку принадлежащие промежутку 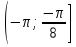 . .Решение.Корни данного уравнения можно найти из соотношения 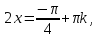 откуда получаем, что откуда получаем, что 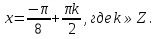 Но 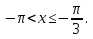 Тогда Тогда 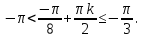 Решим это двойное неравенство: 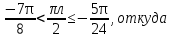 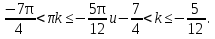 Полученное неравенство выполнено, если k = 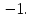 Ответ: 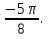 Учитель
Каждому ученику выдается карточка с заданием. Сделав одно задание, ученик передает свою карточку соседу по кругу, вписывая свою фамилию напротив выполненного примера. Карта №1
Карта №2
Карта №3
Карта №4
Карта №5
При проверке работы учитель и ученики-консультанты заполняют таблицу:
5. Подведение итогов. Рефлексия. Учитель: Итак, подведем итоги урока. Решение тригонометрических уравнений состоит из двух этапов. Первый - преобразование уравнения для получения его простейшего вида. 2 Второй - решение полученного простейшего тригонометрического уравнения. Существуют основные методы решения уравнений такого вида: Какие методы решения тригонометрических уравнений мы сегодня повторили? Ответы учащихся:
- сведение к квадратному уравнению; - сведение к однородному уравнению; - универсальная тригонометрическая подстановка. 3.Отбор корней Учитель Оцените свою работу по вашим оценочным листам (дает дополнительные баллы отличившимся ученикам). Рефлексия. Учитель Продолжите фразу:
6. Домашнее задание, инструкция о его выполнении (слайд) Решить уравнение:
№ 23.14 Задачник Алгебра и начала анализа 10 класс, А.Г. Мордкович. При решении первого уравнения воспользуйтесь формулой понижения степени. Литература 1. Алексеев А. Тригонометрические подстановки. // Квант. - 1995. - №2. -с. 40 - 42. 2. Гилемханов Р.Г. О преподавании тригонометрии в 10 классе по курсу В //Математика в школе. 2001-№ 6 -с. 26-28. 3. ЕГЭ. Математика 2008.Сборник экзаменационных заданий. Денищева Л.О., Рязановский А.Р., Семёнов П.В. – М., изд-во «Эксмо-Пресс», 2008. 4. Крамор В.С. Тригонометрические функции. - М.: Просвещение, 1979. 5. Мордкович А.Г. Методические проблемы изучения тригонометрии в общеобразовательной. //Математика в школе. 2002 - № 6 - с.32-38. 6. Мордкович А.Г. Алгебра и начала математического анализа. 10-11 классы. В 2 ч. Ч. 1. Учебник (задачник) для учащихся общеобразовательных учреждений (базовый уровень), - М.: Мнемозина, 2012. 7. Синакевич С.В. Тригонометрические уравнения - М.: Учпедгиз, 1959. 8. Чулков П. В. Уравнения и неравенства в школьном курсе математики. - М.: Педагогический университет «Первое сентября», 2010 Интернет - источники Сайт «Вся элементарная математика» https://bymath.net/studyguide/tri/sec/tri16.ht | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||