Конспект урока по алгебре и началам анализа в 11 «В» классе Тема урока: «Решение логарифмических уравнений и неравенств». Тип урока: урок обобщения и систематизации знаний
 Скачать 35.95 Kb. Скачать 35.95 Kb. |
   Конспект урока по алгебре и началам анализа в 11 «В» классе Конспект урока по алгебре и началам анализа в 11 «В» классеТема урока: « Решение логарифмических уравнений и неравенств» . Тип урока: урок обобщения и систематизации знаний. Цели урока: 1. Обучающие цели: повторение, обобщение и систематизация знаний учащихся по теме «Свойства логарифмической функции» и их применение. Закрепление методов решения логарифмических уравнений и неравенств 2. Развивающие цели: способствование формированию умений применять полученные знания в новой ситуации, развитие математического мышления и речи, развитие навыков использования мультимедиа. 3. Воспитывающие цели: воспитание интереса к математике, активности, мобильности; восприятие компьютера . Формирование навыков адекватной самооценки деятельности. Задачи урока: 1. Проверить усвоение материала по данной теме. 2. Закрепить навыки выполнения заданий по данной теме. 3. Формировать навыки самоконтроля в процессе выполнения заданий. 4. Формировать умение применять знания. Образовательные результаты, которые буду достигнуты учащимися1. Смотр знаний по свойствам с самопроверкой покажет знания учащихся свойств функции, наличие адекватной самооценки деятельности. 2. Спланированное обобщение систематизирует знания, закрепит навыки выполнения заданий, способствует развитию математического мышления и речи. 3. Разнообразие форм работы на уроке способствует формированию умения применять знания в новой ситуации. 4. Использование интерактивных средств обучения развивает интерес к математике и мультимедиа, активизирует и мобилизует, формирует восприятие компьютера как инструмента обучения. Ход урока:
Французский писатель Анатоль Франц (1844-1924 гг.) заметил: «Что учиться можно только весело….. Чтобы переваривать знания, надо поглощать их с аппетитом» Последуем совету писателя – будем на уроке активны, внимательны, будем «поглощать» знания с большим желанием, ведь они скоро вам понадобятся при сдаче ЕГЭ. Перед вами стоит задача – повторить свойство логарифмов, логарифмические функции, типы, методы и особенности решения логарифмических уравнений и неравенств.
Проводится в форме фронтальной работы с классом. Задания устного опроса можно разделить на две части: в первой части проверяются теоретические знания, а во второй части – умение применять эти знания на практике: при решении уравнений, неравенств и выполнении различных заданий. Ученики комментируют свой ответ.
Вторая часть устного опроса проводится после проверки домашнего задания
Всё ли получилось в домашней работе? Это хорошо, но я всё – таки хочу проверить, как вы справились с номером 527(а) 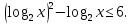 с чего начинают решение логарифмических уравнений и неравенств( ОДЗ) с чего начинают решение логарифмических уравнений и неравенств( ОДЗ)ОДЗ: х > 0; Что мы делаем дальше?( перенос в одну сторону и замена) 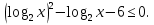 Замена: 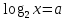 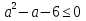 ; ; 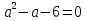 , Д = 1+24 =25 ; а1 = , Д = 1+24 =25 ; а1 = 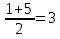 ; а2 = ; а2 = 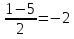 + -2 - 3 = аЄ 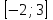 Что мы делаем дальше? ( обратную замену и записываем в виде двойного неравенства) -2 ≤ 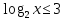 Запишем в виде системы 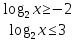 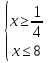 х Є х Є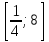 Это удовлетворяет ОДЗ. Это удовлетворяет ОДЗ.
1.Работа 3-х учеников по карточкам индивидуальных заданий. 2.Заполни пропуски: а)Log2 16 = …; б)Log2 1/8 = …; в) Log2 1 = …; г)Log√5 25 = …; д)Log…1/32 = - 5. 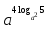 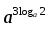 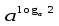 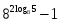 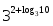 Вычислить: Вычислить: 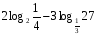 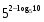 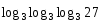 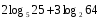 4. Закрепление изученного материала Решить неравенство: 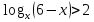 Решение: ОДЗ: 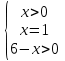 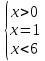 хЄ 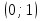 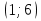 1.х > 1 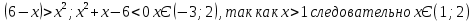 2 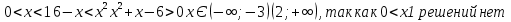 Ответ : ( 1 ; 2) Применение свойств функции при решении логарифмических уравнений и неравенств Какое свойство функции мы достаточно часто применяем при решении различных уравнений и неравенств? Ответ: монотонность В чём оно заключается? Если функция у=f(х) возрастает на промежутке Х, а функция у=g(х) убывает на промежутке Х, то уравнение f(х)=g(х) не может иметь более одного корня на Х. Можем ли мы его применить для решения данных уравнений? Да 5. Решение задач в рамках подготовки к ЕГЭ Сейчас я хочу предложить вам решить некоторые задания по данной теме, встречающиеся в демонстрационных версиях ЕГЭ 2011 Задания В7: 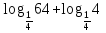 ; ; 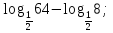 1+ 2 1+ 2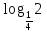 ; ;  В10: Найдите наибольшее значение функции: у = 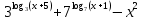 В3: 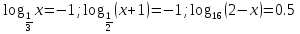 С1: Решение на слайде ( с решением выступает заранее подготовленный ученик) 6.Подведение итогов урока. рефлексия |