Практикум по решению планиметрических задач по теме «Треугольники» в рамках подготовки к егэ
 Скачать 67.36 Kb. Скачать 67.36 Kb.
|
      Нелидова Елена Павловна Нелидова Елена Павловнаучитель математики МБОУ «СОШ №59» г. Брянска класс 10 Тема урока: Практикум по решению планиметрических задач по теме «Треугольники» в рамках подготовки к ЕГЭ. Цели: 1. Образовательные: - повторить и обобщить знания по данной теме; - развивать умения систематизировать теоретический материал, выделять из него наиболее важное и существенное, применять полученные знания на практике; - закрепить навыки решения планиметрических задач. 2. Развивающие: - расширение кругозора учащихся, повышение мотивации к изучению предмета; - стимулирование познавательного интереса, развитие творческих способностей; - развитие умения выделять главное, сравнивать, обобщать изученные факты; - закрепление теоретических знаний и развитие практических навыков и умений; - развитие графической культуры учащихся, геометрического воображения и логического мышления; - формировать потребность в решении геометрических задач в целях подготовки к ЕГЭ и получения дальнейшего образования; - развивать математическую речь, умение слушать, делать логические выводы, аргументировать свою точку зрения. 3. Воспитательные: - формировать умение работать в команде; - воспитывать уважение к чужому мнению, чувства товарищества, сотрудничества, ответственности за общее дело; - развивать познавательный интерес к изучению математики. Задачи, способствующие достижению цели: - сформировать умения применять полученные знания при решении планиметрических задач; - обобщить, систематизировать, знания учащихся по планиметрии; - познакомить учащихся с некоторыми методами и приемами решения планиметрических задач; - побуждать желание выдвигать гипотезы по решению задач и аргументировано доказывать их; - формировать навыки работы с дополнительной научной литературой и другими источниками информации; - способствовать развитию умений работать в малых творческих группах; - научить учащихся применять аппарат алгебры к решению геометрических задач. Умение мыслить математически – одна из благороднейших способностей человека. Д. Б. Шоу. Если вы хотите научиться плавать, смело входите в воду, а если хотите научиться решать задачи, то решайте их. Д. Пойа. (На доске - высказывания ) Ход урока. I. Вводная беседа. Не за горами тот день, когда вы будете сдавать единый государственный экзамен по математике. 30% задач, предлагаемых на экзамене, составляют задачи по геометрии. Известный английский писатель Бернард Шоу говорил: «Умение мыслить математически – одна из благороднейших способностей человека». Вам известны слова венгерского, швейцарского и американского математика Дьердь Пойа: «Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их». Сегодня мы с вами будем учиться смело входить в реку под названием Геометрия и будем учиться преодолевать ее течения, водовороты, чтобы благополучно достичь берега. Игорь Федорович Шарыгин - преподаватель математики, автор многих книг по математике, учебников и учебных пособий считал, что геометрия – витамин для мозга. Слова «Геометрия – витамин мозга» будут эпиграфом нашего урока. II. Организационная. Сегодня мы будем решать задачи по теме «Треугольники» (1 слайд презентации: эпиграф, тема). Работая в группах (3 группы), мы должны повторить и обобщить знания, связанные с данной темой. Мы продолжим развитие умений систематизировать теоретический материал, выделять из него наиболее важное и существенное, применять полученные знания на практике. В конце урока мы с вами закрепим навыки решения задач по данной теме. (на доску - цели урока) III. Формирование умений и навыков. (Работа с учебным пособием «3000 задач») 1. Общее задание для всех групп. Задача 2748 (стр. 453) В треугольнике АВС АВ = ВС = АС = 2 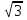 . Найдите высоту СН. (запись условия – на экране) . Найдите высоту СН. (запись условия – на экране)Теперь давайте рассмотрим этапы решения задачи. (учащиеся называют этапы решения задачи) Этапы решения. (этапы решения – на доске по мере озвучивания) 1). Построение рисунка и запись условия задачи. (сначала рисунок: треугольник, равные стороны, высота, потом «дано»: треугольник, стороны, высота, затем «найти». – на экране ) С Дано: ∆АВС, АВ = ВС = АС = 2 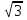 , СН – высота. , СН – высота.2 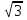 Найти: СН. Найти: СН.А Н В 2). Анализ условия задачи. (этапы анализа условия последовательно появляются на экране)
Вопрос учителя: К нахождению чего сводится наша задача? Ответ учащихся: К нахождению стороны АН. 3). Поиск решения задачи. 1. Рассмотрим ∆АСН. Он прямоугольный, т.к. СН – высота. 2. По т. Пифагора  3. Т. к. по условию треугольник АВС равносторонний и СН – высота, то СН – медиана. Найдем АН. 4. Найдем СН. Во время поиска решения задачи на доске сделать запись (постепенно): ∆АСН- прямоугольный => 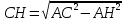 , где , где  . .4). Оформление решения. (самостоятельно с последующей проверкой). Сначала кто-нибудь из учащихся предлагает свою запись решения, потом я показываю на экране. (2 мин) У всех получился такой ответ? (если нет) Почему у тебя ответ не получился? ------------------------------- 2. Задания по группам. Следуя этапам, решить задачи (задача не аналогичная разобранной, одна на все группы). Теперь попробуйте решить задачу № 2385 стр. 419, следуя всем этапам решения задачи. 1 группа представит нам рисунок, запись условия задачи и что надо найти. 2 группа постарается с другими группами проанализировать условие задачи. 3 группа покажет поиск решения и его оформление. Решение задачи должно быть у каждой группы. (На столах, за которыми сидят группы, листы и фломастеры, на которых каждая группа записывает свой этап решения задачи) Каждая группа представляет свой этап решения задачи. Участники других групп задают вопросы ученикам, представляющим работу своей группы. После того, как каждая группа представила выполнение своего задания, проверяется решение задачи. IV. Домашнее задание. Найти другой способ решения каждой из рассмотренных задач. V. Итог. Давайте подведем итог нашей работы. Достигли ли мы поставленных перед нами задач? Скажите, пожалуйста, какие трудности вы испытывали при решении задач? Напишите, пожалуйста на листочках, чем вам сегодняшний урок понравился, чем не понравился. В заключении я хочу вернуться к словам, с которых мы начали урок ( на слайде слова Б. Шоу, Д. Пойа) |