Конспект урока алгебры (10 класс) по теме: "использование свойства ограниченности функций при решении уравнений" цель: познакомить учащихся с нестандартными методами решения уравнений
 Скачать 29.43 Kb. Скачать 29.43 Kb. |
| ПЛАН-КОНСПЕКТ Урока алгебры (10 класс) по теме: "ИСПОЛЬЗОВАНИЕ СВОЙСТВА ОГРАНИЧЕННОСТИ ФУНКЦИЙ ПРИ РЕШЕНИИ УРАВНЕНИЙ" ЦЕЛЬ: познакомить учащихся с нестандартными методами решения уравнений. ЗАДАЧИ:
ХОД УРОКА:
Найдите множество значений функции. Определите, является ли функция ограниченной?
На доске записываем уравнение: Задание: Как, используя свойство ограниченности функций, можно решить уравнение? Деятельность учащихся и учителя. Учащиеся делятся на группы и приступают к обсуждению методов решения. Когда большинство групп закончили микродискуссию, приступаем к обсуждению метода решения. В процессе обсуждения учащимися составляется план решения:
Оформление записи: 1) 2) 3) g(x) = h(x) при g(x) = 0 и h(x) = 0 4) g(-1) = 0, h(-1) = 0, следовательно, х = -1 – корень уравнения. Ответ: -1.
1. а) б) в) Ответ: нет решений. 2. а) б) в) г) Ответ: х =3. 3. 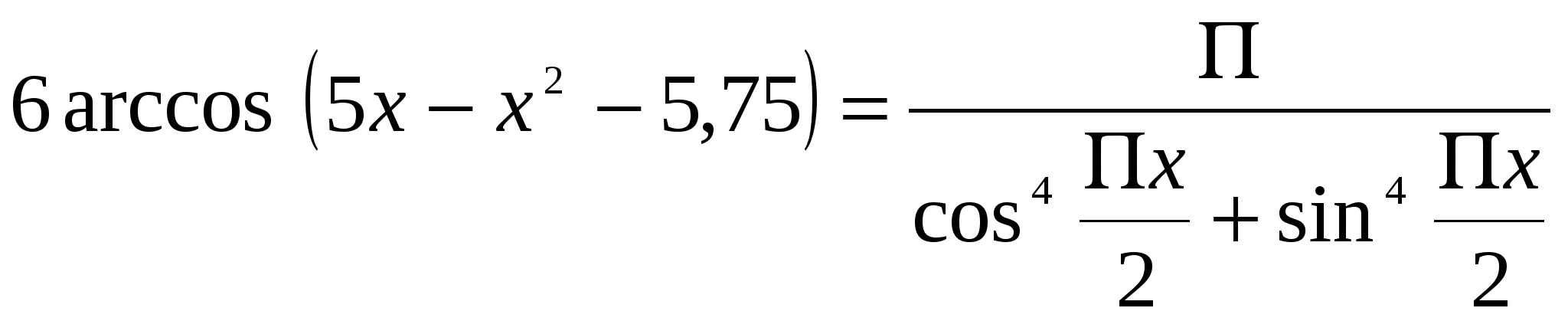 (обсуждение по группам) (обсуждение по группам)а) б) 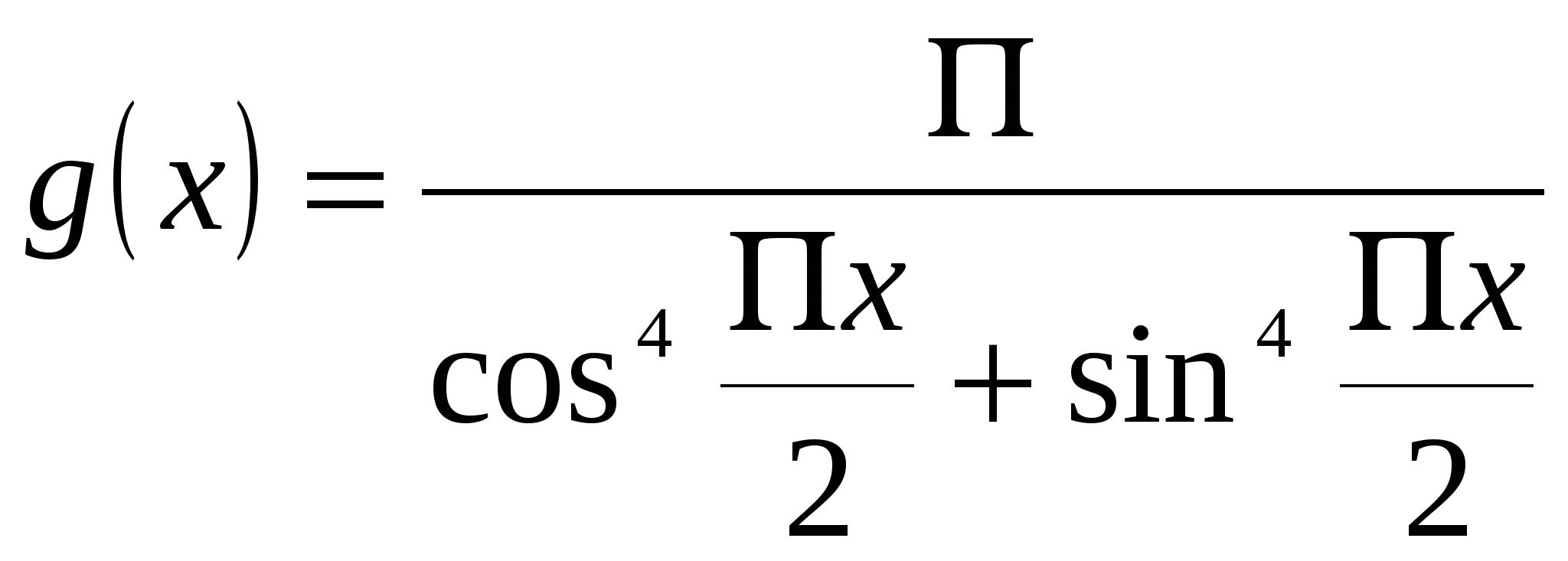 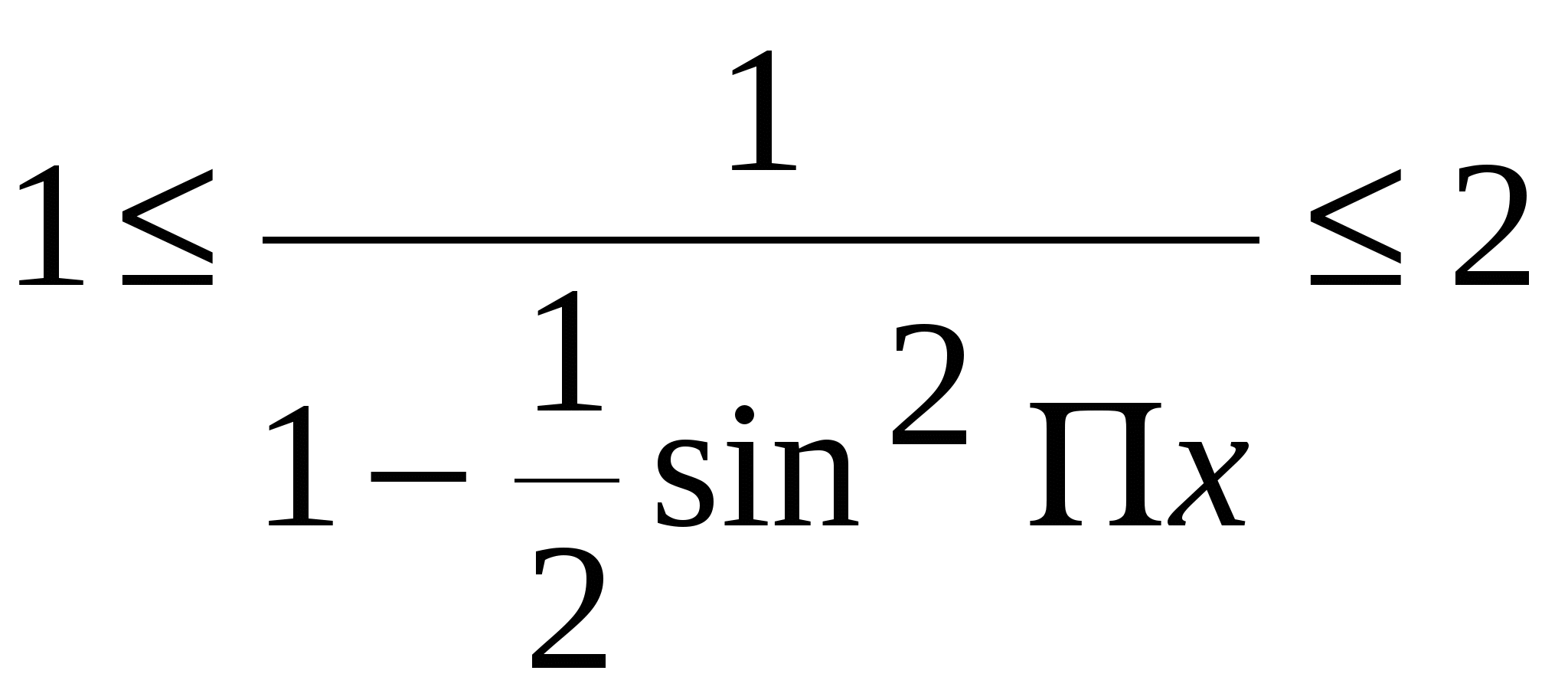 , , 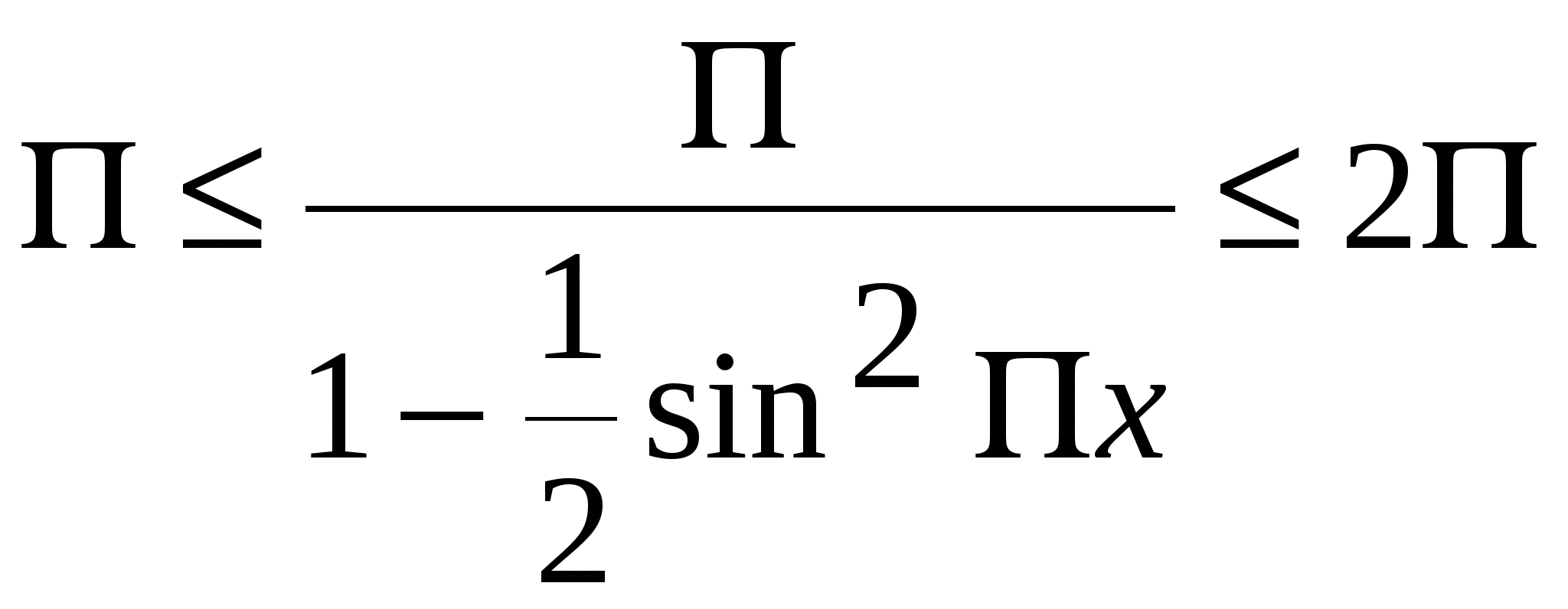 в) Найдем 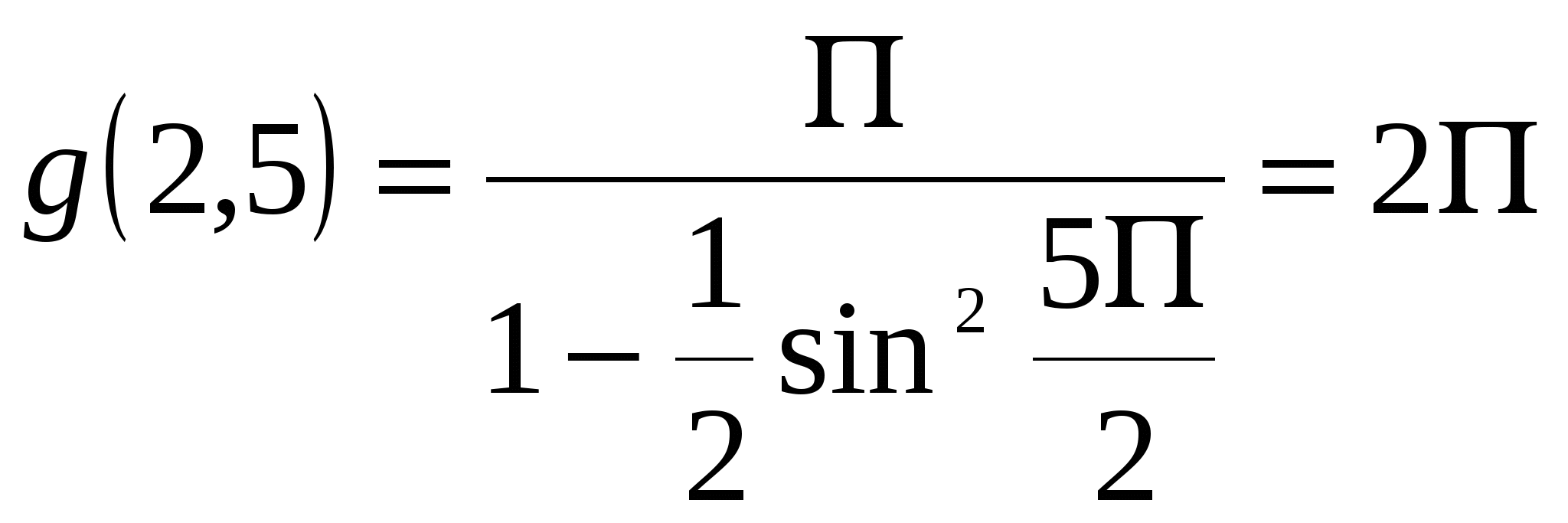 → x=2,5 – корень уравнения. → x=2,5 – корень уравнения.Ответ: 2,5
|