Исследования
 Скачать 352.86 Kb. Скачать 352.86 Kb.
|
| Особенности преподавания комбинаторики, теории вероятностей и статистики в основной школе Содержание Введение. Часть 1. Анализ учебно-методической литературы по теме исследования. 1. Анализ статей из журналов «Математика в школе». 2. Анализ вероятностно-статистической линии в учебной литературе. 3. Некоторые выводы содержательно-методического характера по реализации стохастической линии в основной школе. Часть 2. Методика изучения стохастики в основной школе (на примере 5-6 классов). 1. Методика реализации стохастической линии в 5 классе. 2. Методика реализации стохастической линии в 6 классе. Заключение. Список литературы. Приложение. Пособие для учителя «Комбинаторика в 5-6 классах». Введение В настоящее время никто не подвергает сомнению необходимость включения стохастической линии в школьный курс математики. О необходимости изучения в школе элементов теории вероятностей и статистики речь идет очень давно. Ведь именно изучение и осмысление теории вероятностей и статистических проблем особенно нужно в нашем перенасыщенном информацией мире. Но внедрение стохастической линии в школьный курс столкнулось с некоторыми трудностями, в первую очередь, это методическая неподготовленность учителей и отсутствие единой методики и школьных учебников. Современная концепция школьного математического образования ориентирована, прежде всего, на учет индивидуальности ребенка, его интересов и склонностей. Этим определяются критерии отбора содержания, разработка и внедрение новых, интерактивных методик преподавания, изменения в требованиях к математической подготовке ученика. И с этой точки зрения, когда речь идет не только об обучении математике, но и формировании личности с помощью математики, необходимость развития у всех школьников вероятностной интуиции и статистического мышления становится насущной задачей. Причем речь сегодня идет об изучении вероятностно-статистического материала в обязательном основном школьном курсе «математике для всех» в рамках самостоятельной содержательно-методической линии на протяжении всех лет обучения. Исследования психологов (Ж.Пиаже, Е.Фишбейн) показывают, что человек изначально плохо приспособлен к вероятностной оценке, к осознанию и верной интерпретации вероятностно-статистической информации. Работы психологов утверждают, что наиболее благоприятен для формирования вероятностных представлений возраст 10-13 лет (это 5-7 классы). Экспериментальная работа в 5 и 6 классах по пропедевтике вероятностных представлений, проведению экспериментов со случайными исходами и обсуждению на качественном уровне их результатов показало, что этот не закрепленный формальными «обязательными результатами» период дает хорошее развитие вероятностной интуиции и статистических представлений детей. Часть 1. Анализ учебно-методической литературы 1. Анализ статей из журналов «Математика в школе». Журналы «Математика в школе» содержат ряд статей, в которых рассматриваются различные вопросы по данной теме. О необходимости изучения в школе элементов теории вероятностей и статистики речь идет очень давно. И авторы многих статей говорят о необходимости введения стохастической линии в основную школу. 1. Социально-экономическая ситуация. «Нужно научить детей жить в вероятностной ситуации. То есть нужно научить их извлекать, анализировать и обрабатывать информацию, принимать обоснованные решения в разнообразных ситуациях со случайными исходами. Ориентация на многовариантность возможного развития реальных ситуаций и событий, на формирование личности, способной жить и работать в сложном, постоянно меняющемся мире, с неизбежностью требует развития вероятностно-статистического мышления у подрастающего поколения» (Бунимович). 2. Универсальность вероятностных законов. «Они стали основой описания научной картины мира. Современная физика, химия, биология, демография, социология, лингвистика, философия, весь комплекс социально-экономических наук построен и развивается на вероятностно-статистической базе. Подросток в своей жизни ежедневно сталкивается с вероятностными ситуациями. Игра и азарт составляют существенную часть жизни ребенка. Круг вопросов, связанных с соотношениями понятий «вероятность» и «достоверность», проблема выбора наилучшего из нескольких вариантов решения, оценка степени риска и шансов на успех, представление о справедливости и несправедливости в играх и в реальных жизненных коллизиях – все это, несомненно, находится в сфере реальных интересов подростка». 3. Развивающая роль стохастики. «Преподавание любого раздела математики благотворно сказывается на умственном развитии учащихся, поскольку прививает им навыки ясного логического мышления, оперирующего четко определенными понятиями. Все сказанное в полной мере относится и к преподаванию теории вероятностей, но обучение «законам случая» играет несколько большую роль и выходит за рамки обычного. Слушая курс теории вероятностей, учащийся познает, как применять приемы логического мышления в тех случаях, когда приходится иметь дело с неопределенностью (а такие случаи возникают на практике почти всегда)». 4. Прикладной характер законов теории вероятностей. «Выводы теории вероятностей находят применение в повседневной жизни, науке, технике и т.д. В повседневной жизни нам постоянно приходится сталкиваться со случайностью, и теория вероятностей учит нас, как действовать рационально с учетом риска, связанного с принятием отдельных решений. Хорошим примером применения теории вероятностей в повседневной жизни может служить выбор наиболее целесообразной формы страхования. При планировании, например, семейного бюджета зачастую приходится оценивать расходы, носящие в известной мере случайный характер. Знакомство на том или ином уровне с законами случая необходимо каждому. Применение теории вероятностей в науке, технике, экономике и т.д. приобретает все возрастающее значение. Именно поэтому у все большего числа людей в процессе работы возникает необходимость в изучении теории вероятностей. Современный образованный человек независимо от профессии и рода занятий должен быть знаком с простейшими понятиями теории вероятностей. В наши дни, когда прогноз погоды содержит сообщение о вероятности дождя на завтра, каждый должен знать что собственно это означает». 2. Анализ вероятностно-статистической линии в учебной литературе При введении любой новой темы, любого нового вопроса в основной курс школы встает проблема изложения данного вопроса в школьных учебниках. К реализации нового содержания в действующих учебниках авторы подошли по-разному. В одних учебниках элементы стохастики включены в основное содержание отдельными параграфами. Авторы же других учебников издают новое содержание в форме вкладышей – дополнительных глав к своим пособиям. Попытка построения вероятностно-статистической линии в базовом курсе математики основной школы предпринята в учебниках Под редакцией Г.В Дорофеева и И.Ф Шарыгина «Математика5», «Математика6», «Математика7», «Математика8» и «Математика 9». 5 класс начинается с комбинаторики, где на конкретных задачах и примерах рассматривается решение комбинаторных задач методом перебора возможных вариантов. Этот метод иллюстрируется с помощью построение дерева возможных вариантов. Примеры и задачи очень простые, позволяющие на этапе знакомства с комбинаторными задачами, усвоить принцип простого, упорядоченного перебора возможных вариантов. В пункте «Случайные события» рассматривается понятие случайное событие, достоверные, невозможные и равновероятные события. Тут же приводятся реальные, понятные примеры, позволяющие учащимся лучше усвоить эти понятия. В последней главе учебника рассматриваются таблицы и диаграммы (как способ представления информации). Учащихся учат пользоваться таблицей, извлекать из нее и анализировать необходимую информацию, также учат самих строить таблицы. В пятом классе рассматриваются столбчатые диаграммы, в одной из задач рассмотрена круговая диаграмма. Также рассматривается пункт «Опрос общественного мнения», где составление таблиц по данным опроса позволяет решить те или иные классные вопросы, возникающие в реальной жизни 6 класс начинаем с повторения таблиц и диаграмм. Повторяют уже изученные столбчатые диаграммы и более подробно рассматривают круговые (для представления соотношения между частями целого). Далее идут 2 параграфа по комбинаторике: логика перебора и правило умножения. Здесь рассматриваются задачи, которые решаются уже известным им способом перебора и предлагается упростить его, используя, так называемое кодирование. Также рассматривается новый способ решения комбинаторных задач с помощью правила умножения. Завершается учебник главой - «вероятность случайных событий». Учащимся предлагается провести ряд экспериментов, зафиксировав результаты в таблицах. После чего, используя полученные результаты, вводится понятие частота и вероятность случайных событий 7 класс начинается с рассмотрения основных статистических характеристик: среднее арифметическое, мода, размах, опять же с множеством примеров из жизни. В одном из параграфов снова обращаемся к решению комбинаторных задач, которые решаются с помощью рассуждений. Рассматриваются перестановки. И заключительная глава продолжает рассматривать вероятность и частоту случайных событий. В 8 классе сначала повторяются статистические характеристики, изученные в 7 классе, и вводится новая характеристика – медиана. Рассматриваются таблицы частот. Приводятся примеры, показывающие связь с практикой, описываются различные жизненные ситуации. В 8 классе вводится классическое определение вероятности, данное Лапласом. Рассматриваются геометрические вероятности. В учебнике 9 класса рассматриваются статистические исследования, вводится определение статистики. В главе рассматриваются доступные учащимся примеры статистических исследований, в ходе которых используются полученные ранее знания о случайных экспериментах, способах представления данных и статистических характеристиках. Вводятся новые понятия выборка, репрезентативность, генеральная совокупность, ранжирование, объем выборки. Рассматривается новый способ графического представления результатов – полигоны. Вводятся понятия выборочной дисперсии и среднее квадратичное отклонение. В учебнике рассматриваются 3 примера статистических исследований, это реальные примеры близкие школьнику. Это вопросы: «Как исследуют качество знаний школьников», «Удобно ли расположена школа?», «Куда пойти работать?». Учащийся видит применение знаний по статистике в реальных жизненных ситуациях. Изучив, данный комплект учебников, можно отметить несколько моментов. Во-первых, курс рассчитан на 5- 9 классы, в то время, как большинство других учебных пособий предлагает рассматривать эти вопросы лишь с 7 по 9 классы. Во-вторых, что тоже отличает предложенный в этих учебниках курс от других, это параллельное изложение линий. Зубарева И.И., Мордкович А.Г. «Математика 5», «Математика 6». В 5 классе последняя глава «введение в вероятность» содержит 2 параграфа. В одном параграфе рассматриваются достоверные, невозможные и случайные события. И даны задачи на определение характера события (достоверное, невозможное или случайное). Во втором параграфе рассматриваются комбинаторные задачи, решаемые методом перебора возможных вариантов. В 6 классе авторы знакомят с понятием вероятность. Даны упражнения на определение степени вероятности того или иного события, выполнять которые учащиеся должны с опорой на интуицию. В следующем пункте вводится классическое определение вероятности. Рассматриваются задачи, в которых для вычисления вероятности используют комбинаторное правило умножения. По-моему мнению, рассматриваемые комбинаторные задачи, решаемые методом перебора возможных вариантов, взяты не совсем удачно. Для первого знакомства с задачами на перебор возможных вариантов лучше взять более простые задачи. Еще одним недостатком, на мой взгляд, является то, что авторами вводится лишь классическое определение вероятности и абсолютно не рассматривается понятие частоты. А более логично и целесообразно вводить классическое определение на основе частотного. Некоторые учебные комплекты пополнились дополнительными учебными пособиями, содержащими материал по стохастике. Макарычев Ю.Н., Миндюк Н.Г. «Алгебра: элементы статистики и теории вероятностей». Под редакцией Теляковского С.А. Это учебное пособие предназначено для учащихся 7-9 классов, оно дополняет учебники: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. «Алгебра 7», «Алгебра 8», «Алгебра 9», под редакцией Теляковского С.А. Книга состоит из четырех параграфов. В каждом пункте содержатся теоретические сведения и соответствующие упражнения. В конце пункта приводятся упражнения для повторения. К каждому параграфу даются дополнительные упражнения более высокого уровня сложности по сравнению с основными упражнениями. В 7 классе (§1) материал объединен в параграф «статистические характеристики», который знакомит с простейшими статистическими характеристиками (среднее арифметическое, мода, медиана, размах). Упражнения к параграфу можно разделить на 2 группы. Первую группу составляют задания на отыскание рассматриваемых характеристик и истолкование их практического смысла. Ко второй группе относятся задания, которые требуют не только знания определений изучаемых статистических характеристик, но и умений проводить необходимые рассуждения, использовать ранее введенный алгебраический аппарат. Материал, изучаемый в 8 классе (§2) также объединен в один параграф «Статистические исследования», где рассматриваются вопросы организации статистических исследований и наглядного представления статистической информации (таблицы частот). Сначала повторяются основные статистические характеристики. Вводятся новые понятия: интервальный ряд, сплошное и выборочное исследования, выборка, генеральная совокупность, репрезентативность. Знакомство с новыми видами наглядной интерпретации результатов статистических исследований – полигонами и гистограммами Наибольший объем материала приходится на 9 класс. Здесь есть 2 параграфа. §3 «Элементы комбинаторики» содержит 4 пункта:
§4 «Начальные сведения из теории вероятностей». Изложение материала начинается с рассмотрения эксперимента, после чего вводят понятие «случайное событие» и «относительная частота случайного события». Вводится статистическое и классическое определение вероятности. Параграф завершается пунктом «сложение и умножение вероятностей». Рассматриваются теоремы сложения и умножения вероятностей, вводятся связанные с ними понятия несовместные, противоположные, независимые события. Этот материал рассчитан на учащихся, проявляющих интерес и склонности к математике, и может быть использован для индивидуальной работы или на внеклассных занятиях с учащимися. В данном пособии некоторые элементы вводятся таким же образом, как и в учебном комплекте Дорофеева. Но материал сокращен, за исключением комбинаторики, которая содержит больше и теории и практических упражнений. По моему мнению, комбинаторика и начальные сведения из теории вероятностей предлагается изучать слишком поздно. Как уже отмечалось выше, начинать обучать комбинаторике и формировать первые вероятностные представления лучше как можно раньше. 3. Некоторые выводы содержательно-методического характера по реализации стохастической линии в основной школе На основе всего рассмотренного и изученного материал по предложенной теме, можно сделать некоторые выводы и дать рекомендации по реализации стохастической линии в школе. Анализ учебной литературы по исследуемой теме показал, что разные авторы подошли к реализации нового содержания в учебниках по-разному. Опираясь на государственные стандарты образования, анализ учебной и методической литературы, можно выделить следующие моменты о содержании и последовательности изложения материала по данной линии. Во-первых, необходимо изучать этот материал на протяжении всего курса средней школы. Весь курс условно можно разбить на несколько этапов (5-6 классы (подготовительный); 7-8 классы; 9 класс), причем на каждом этапе формируются одни и те же виды деятельности, но на разных уровнях и различными средствами. На каждом этапе материал усложняется, дополняется, отрабатываются ранее усвоенные и формируются новые умения и навыки. Важным элементом стохастической линии является работа с данными: сбор данных, обработка, представление, анализ, практические выводы. Всем этим занимается наука, которая называется статистика. На первом (подготовительном) этапе обучения - это работа с таблицами и диаграммами. Необходимо обучать учащихся не только работе с уже готовыми данными, но и самостоятельно собирать информацию и представлять ее в различных формах. Ежедневно нам необходима разнообразная информация, которая может быть представлена в различной форме, и одним из самых распространенных способов представления информации являются таблицы. Учащиеся в своей жизни часто сталкиваются с различного рода таблицами – это расписание уроков, страница классного журнала, программа телепередач, турнирные таблицы и т.п. Учащиеся должны уметь анализировать данные, используя таблицы и диаграммы. Это позволяет в дальнейшем при изучении статистики не останавливаться на обучении учащихся работе с табличными данными и позволяет сконцентрировать внимание именно на обучении учащихся делать статистические и практические выводы. Можно показать практическую значимость таблиц, построенных по результатам опроса общественного мнения (в классной жизни такие таблицы могут быть использованы, например, для организации досуга). Для представления различных данных также очень удобно использовать диаграммы. Диаграмма является очень наглядным способом представления информации и различных данных и позволяет легче анализировать полученные результаты. Одним из направлений стохастической линии является теория вероятностей, где одной из важных задач на первом этапе является формирование понятия - вероятность случайного события. Сначала необходимо познакомить учащихся с понятием случайное событие, сформировать у них представление о том, какое событие называется достоверным, какое невозможным и какие события называются равновероятными. Все эти понятия нужно вводить, опираясь на понятные примеры, и просить детей самих приводить такие примеры. Учитель должен все время фиксировать внимание учащихся на случайных явлениях в быту, в природе и технике. Необходимо развить у учащихся понимание степени случайности различных явлений и событий. При этом учитель сам должен качественно оценивать ответ, так как часто ответ является субъективным. Перед введением самого понятия - вероятность случайного события полезно провести эксперименты со случайными исходами. После проведения экспериментов можно познакомить учащихся с результатами экспериментов, которые неоднократно проводились на протяжении нескольких столетий и сравнить c результатами, полученными учащимися. Сравнивая их, учащиеся с удивлением замечают, что результаты очень похожи. Проведение экспериментов должно возбудить у учащихся неподдельный интерес. Эксперимент является эмпирическим методом обучения, используемый в частности, в экспериментальных естественных науках, а математика не является экспериментальной. Поэтому этот метод в математике применяется редко, так как опыт не является достаточным основанием истинности того или иного предложения. Но опыт, эксперимент дает учащимся возможность извлечь из них очевидные закономерности, сделать какие то открытия, а теория вероятностей опирается именно на результаты многочисленных экспериментов. В ходе экспериментов, вводится понятие частоты (отношение количества благоприятных исходов испытаний к количеству всех проведенных испытаний) и вероятности данного события. При проведении опытов учащиеся могут убедиться в действии следующего закона: с увеличением числа подбрасываний значения статистической частоты, выбранного для наблюдения исхода, устойчиво сосредотачивается возле некоторого числа р, которое и называют вероятностью наблюдаемого исхода или события. То есть частота появления некоторого случайного события, при проведении эксперимента, позволяет вычислить статистическую вероятность этого события, на практике статистические испытания и наблюдения являются основным способом оценки вероятностей события. Но нужно отметить, что говорить о статистической вероятности мы можем лишь при проведении достаточно большого числа экспериментов. Поэтому всегда возникает вопрос о точности такой оценки вероятности, поскольку не всегда возможно проведение достаточно большого числа экспериментов. Оценку вероятности того или иного случайного события можно сделать, основываясь на результатах ранее проведенных экспериментов. Параллельно с вероятностной линией должна изучаться и комбинаторика. Оптимальный вариант, если работа по формированию комбинаторного мышления начнется уже с начальных классов. Начинать обучение комбинаторике целесообразно с решения простых комбинаторных задач методом непосредственного перебора. Операция перебора раскрывает идею комбинирования, служит основой для формирования комбинаторных понятий и хорошей подготовкой к выводу комбинаторных формул и закономерностей. Основными комбинаторными понятиями являются сочетания, перестановки и размещения. Но на первом этапе сами термины можно не вводить, главное, чтоб учащийся осознавал, наборы какого типа требуется составить в данной задаче (важен ли порядок и возможны ли повторения). После того как учащиеся научаться составлять наборы из элементов заданного множества по заданному свойству, на первый план выходит задача по подсчету количества возможных наборов. Такие комбинаторные задачи решаются с помощью рассуждений, раскрывая принцип умножения. Хорошей наглядной иллюстрацией правила умножения является дерево возможных вариантов. Очень важно показать его применение при решении комбинаторных задач. Первое знакомство со статистикой происходит при изучении основных статистических характеристик, их нахождение и использование для анализа и практических выводов. При изучении основных статистических характеристик важно понимать их практическую значимость, нужно уметь использовать их для анализа имеющейся информации и делать правильные выводы на их основе. В продолжении вероятностной линии следующим шагом идет введение классического определения вероятности. Необходимо, чтобы учащиеся понимали разницу между статистическим и классическим определениями вероятности. Чтобы они осознавали, что это не еще одно определение вероятности, а один из способов вычисления вероятности. Таким образом, сопоставляя определение классической вероятности и относительной частоты (статистическая вероятность), заключаем: определение классической вероятности не требует, чтобы испытания производились в действительности; определение же статистической вероятности предполагает, что испытания были произведены фактически. Другими словами, классическую вероятность вычисляют до опыта, относительную частоту – после опыта. После введения классического определения вероятности можно рассмотреть геометрическую вероятность. Геометрическая вероятность напоминает классическую, но при геометрическом подходе количество всех возможных и благоприятных исходов бесконечно. В этом случае рассматривается не количество возможных и благоприятных исходов, а отношение площади области, благоприятствующей появлению рассматриваемого случайного события, к площади всей области. То есть геометрическое определение вероятности является обобщением классического определения на случай, когда число равновозможных исходов бесконечно. На последующих этапах переходим к изучению непосредственно статистики, используя ранее полученные знания. Появляется много новых терминов, и учителю можно посоветовать следующее: во-первых, можно сделать таблицу аналогичную таблице приведенной в учебнике Мордковича, Семенова [23], во-вторых, очень полезно было бы завести всем учащимся словарики, куда бы они заносили новые понятия, по мере потребности, могли бы туда заглядывать. Статистические исследования являются завершающим фрагментом вероятностно-статистической линии курса. Здесь рассматриваются доступные учащимся примеры комплексных статистических исследований, в ходе которых используются полученные ранее знания. Также вводятся некоторые новые понятия. Изучение этого материала направлено на формирование умения понимать и интерпретировать статистические результаты. Часть 2. Методика изучения стохастики в основной школе. В данной главе на основе выводов, полученных в 1 части, предлагается методика по реализации стохастической линии в 5-6 классах. 1. Методика реализации стохастической линии в 5 классе Основными задачами на этом этапе являются:
Формирование комбинаторных навыков, как уже говорилось в 1 главе, нужно начинать как можно раньше. Желательно вести пропедевтическую работу уже в начальных классах. А в 5 классе предлагаются простейшие комбинаторные задачи, решая которые должна вестись либо работа по перебору возможных вариантов, либо по упорядочиванию, либо их объединение - перебор и упорядочивание вместе. В нашей жизни часто возникают такие задачи, которые имеют несколько различных решений, и перед нами встает проблема рассмотреть все возможные варианты решения. Для этого нам нужно найти удобный способ перебора, при котором будут рассмотрены всевозможные варианты, и они не повторялись бы. На первом месте перед учителем стоит задача по формированию навыков систематического перебора. Начинать нужно с простых задач, где не так много элементов, важна сама суть перебора всех вариантов. Три друга, Антон, Борис и Виктор, приобрели два билета на футбольный матч. Сколько существует различных вариантов похода на футбол? Здесь необходимо перебрать всевозможные пары мальчиков. После этого можно добавить условие, при котором, решая задачу, учитываем еще и место, на котором будет сидеть тот или иной мальчик, то есть учитывается порядок элементов в наборе. Три друга, Антон, Борис и Виктор, приобрели два билета на футбольный матч на 1-е и 2-е места первого ряда стадиона. Сколько существует способов занять эти два места на стадионе? Записать все эти варианты. Здесь мы можем использовать результаты предыдущей задачи. В ней мы не учитывали порядок, а теперь необходимо учитывать порядок, на каком месте будет сидеть тот или иной мальчик. Рассмотрим тот вариант, когда на матч пошли Антон и Борис, в этом случае возможно два варианта занять места на матче: 1-ое место – Антон, 2-ое место - Борис и наоборот 1-ое место Борис, а 2-ое Антон. То есть упорядочить два элемента мы можем двумя способами. Таким образом, решение предыдущей задачи дало нам два решения для этой задачи. Аналогично на каждый вариант предыдущей задачи мы получаем еще один вариант решения, итого 6 вариантов. Антону, Борису и Виктору повезло, они купили 3 билета на футбол на 1-е, 2-е и 3-е места первого ряда стадиона. Сколькими способами могут занять мальчики эти места? В данной задаче, как и в предыдущей важно на каких местах сидят мальчики, то есть нам нужно рассмотреть, сколько существует вариантов рассадить трех мальчиков на три разных места. Пусть на первом месте сидит Антон, тогда на оставшиеся два места двух оставшихся мальчиков мы можем усадить двумя способами, аналогично для случаев, когда на первом месте сидит Борис и Виктор. В результате получим 6 вариантов, то есть упорядочить 3 элемента мы можем шестью способами. В предыдущих задачах, не учитывая порядка перебора не сложно перечислить все возможные варианты, так как их не так много, но часто при переборе возможных вариантов их может быть столько, что сложно оценить все ли возможные решения мы учли и не пропустили ли хотя бы одно из них. В этом случае необходимо упорядочить процедуру перебора, то есть перебирать возможные варианты в некотором порядке, определенном заранее, который позволяет не допускать повторений решений и пропускать возможные решения. Сколько двузначных чисел можно составить, используя цифры 1,2,3. Выпишем возможные двузначные числа. Но мы не будем выписывать эти числа как попало, а договоримся выписывать их в порядке возрастания, что позволит нам не пропускать числа и не повторяться. В процессе решения этой задачи может возникнуть такой вопрос, а может ли одна и та же цифра повторяться в числе два раза? (если не возникнет, то учитель может сам обратить на это внимание). Так как в данной задаче это условие не оговорено, то решим ее для обоих случаев, и увидим, что в каждом из них число решений различно. Из чего делаем вывод, что данное условие при решении задач необходимо учитывать. В алфавите племени УАУА имеются только две буквы – «а» и «у». Сколько различных слов по три буквы в каждом можно составить, используя алфавит этого племени? В этой задаче одна и та же буква может встречаться в слове как один, так два или три раза. И нужно рассмотреть все варианты. Заметим, что очень удобно процесс перебора осуществлять путем построения специальной схемы, которая называется дерево возможных вариантов. Рассмотрим построение дерева возможных вариантов для данной задачи: сначала нужно выбрать первую букву – это могут быть буквы «а» или «у», поэтому в «дереве» из корня проведем две веточки с буквами «а» и «у» на концах. Вторая буква может быть опять как «а» так и «у», поэтому из каждой веточки выходит еще по две веточки и т.д. 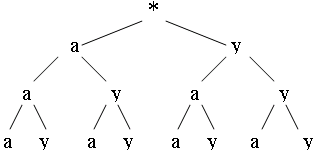 Теперь, проходя по веточкам дерева, по порядку выписываем нужные нам сочетания букв - «слова»: ааа; аау; ауа; ауу; уаа; уау; ууа; ууу. Дерево помогает увидеть путь решения, учесть все варианты и избежать повторений. Нужно обратить внимание, что дерево возможных вариантов позволяет нам подсчитывать упорядоченные наборы В 5 классе начинается работа по формированию вероятностных представлений у учащихся. Сначала рассмотрим понятие случайное событие. Часто в жизни мы употребляем такие слова, как «возможно», «это невероятно», «это маловероятно» и т.д. Подобные выражения мы используем, когда говорим о событии, которое в одних условиях может произойти, а может и не произойти. Такие события называют случайными. События, которые при данных условиях обязательно происходит, называют достоверным. События, которые при данных условиях не могут произойти, называют невозможными. Для отработки данных понятий можно рассмотреть упражнения, в которых нужно определить является событие достоверным, невозможным или случайным. Оцените, какие из перечисленных событий являются достоверными, какие невозможными, а какие случайными и почему вы так считаете: А) при бросании кубика вы получите шестерку; Б) при бросании кубика вы получите число больше 6; В) при бросании кубика вы получите четное число; Г) при бросании кубика вы получите число, которое делится на 7 Д) при бросании кубика вы получите число больше 1; Е) при бросании кубика вы получите нечетное число; Ж) кубик, упав, останется на ребре. В мешке лежит 10 шаров: 3 синих, 3 белых и 4 красных. Какие из следующих событий являются случайными, достоверными и невозможными и почему вы так считаете: А) из мешка вынули 4 шара и все они синие; Б) из мешка вынули 4 шара и все они красные; В) из мешка вынули 4 шара, и все они оказались разного цвета; Г) из мешка вынули 4 шара, и среди них не оказалось шара черного цвета; Ученик задумал натуральное число. Какие из следующих событий будут достоверными, невозможными и случайными и почему вы так считаете. А) Задумано четное число; Б) Задумано число, не являющееся ни четным, ни нечетным; В) Задумано нечетное число; Г) задумано число, являющееся четным или не четным. События А и В являются случайными, так как может быть загадано как четное, так и нечетное число. Возникает вопрос, какое из событий более вероятно: задумано четное число или задумано нечетное число. Так как чисел четных и нечетных одинаковое количество, то оба эти события имеют равные шансы. Такие события называются равновероятными. Также о некоторых случайных событиях мы можем сказать, что оно «маловероятно» или «очень вероятно». Укажите, какие из следующих событий – невозможные, достоверные, случайные, а о каких мы можем сказать, что оно «маловероятно» или «очень вероятно»:
Важно уже в 5 классе давать учащимся задачи следующего плана: Данила и Наташа заспорили, кто из них будет первым читать интересную книгу. Тогда Наташа предложила сыграть в игру и книгу отдать победителю. Они взяли вертушку, которая изображена на рис.1, 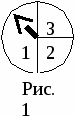 и установили следующие правила игры: каждый из них поочередно крутит вертушку; если стрелка останавливается в области 1, то 1 очко получает Наташа, а если – в области 2, то 1 очко получает Данила. Если стрелка попадает в область 3, то никто из ребят не получает очков. Кто первым наберет 20 очков, тот считается победителем и получает книгу. Как вы думаете, при таких правилах игра будет справедливой? и установили следующие правила игры: каждый из них поочередно крутит вертушку; если стрелка останавливается в области 1, то 1 очко получает Наташа, а если – в области 2, то 1 очко получает Данила. Если стрелка попадает в область 3, то никто из ребят не получает очков. Кто первым наберет 20 очков, тот считается победителем и получает книгу. Как вы думаете, при таких правилах игра будет справедливой? Учащиеся еще не знакомы с понятием вероятность и при ответе на вопрос должны опираться на свою интуицию. Они должны понимать, что у Наташи больше шансов выиграть, чем у Данилы, так как область 1 в два раза больше, чем область 2, и больше вероятности, что вертушка остановится в области 2. Очень важным элементом стохастики является анализ данных и начальным этапом анализа данных является работа с таблицами и диаграммами, которую необходимо начинать в 5 классе. Начинать рассмотрение таблиц нужно с рассмотрения уже известных учащимся таблиц, в частности: страница классного журнала, расписание уроков и т.п. С такими таблицами учащиеся чаще всего уже уметь работать и извлекать из нее всю необходимую им информацию. Часто в таблице для анализа информации необходимо бывает просуммировать содержащиеся в ней данные. Поэтому часто в таблицу включен столбик или строка «Всего» или «Итого», которые содержат полученные суммы. В таблице№1 представлены результаты наблюдений за погодой в течение четырех месяцев. Таблица №1.
Заполните последний столбец. Используя таблицу, ответьте на следующие вопросы:
Здесь и работа со строками и со столбцами, и подсчет суммы нескольких ячеек. Рассмотрим пример, показывающий практическую ценность сбора и анализа статистических данных. Вы решили в свободное время собраться классом и организовать некоторое классное мероприятие, но еще не решили, что именно. Было бы целесообразным учесть мнение большинства учащихся класса, а для этого нужно провести опрос: «Как бы вы хотели провести свободное время классом?» и предложить варианты ответов. Результаты нужно занести в таблицу. Например, получили следующие результаты: Таблица №2.
Рассматривая эту таблицу, мы делаем вывод, что лучше всего будет сходить в поход, так как большинством учащихся класса был выбран именно этот вариант. Таблица является одним из способов представления информации, но более наглядным является графическое представление данных. Это различные диаграммы: линейные, столбчатые и круговые. Построим столбчатую диаграмму по нашей таблице: 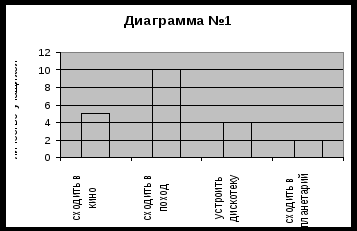 По диаграмме мы сразу видим, что большинство учащихся хочет сходить в поход. И лишь два человека желают посетить планетарий. Для представления соотношения между частями некоторого единого целого, удобно пользоваться круговыми диаграммами. Для нашего примера она будет выглядеть следующим образом:  2. Методика реализации стохастической линии в 6 классе Основные задачи:
В 6 классе в теме комбинаторика продолжаем рассматривать комбинаторные задачи, на первый план выходят задачи по подсчету числа возможных вариантов. Существует несколько подходов к преподаванию комбинаторики: теоретико-множественный, лексико-графический и теоретико-вероятностный. В школе преимущество отдается теоретико-множественному подходу, но будет полезным частично обратиться и к лексико-графическому подходу. При таком подходе все определения опираются на представление об алфавите, словах, длине слов и др. Решая задачи, иногда очень удобно использовать кодирование, то есть обращение к лексико-графическому подходу. Рассмотрим следующую задачу: несколько стран решили использовать для своего государственного флага символику в виде трех горизонтальных полос одинаковой ширины разных цветов – белого, синего, красного. Сколько стран могут использовать такую символику при условии, что у каждой страны – свой флаг. Мы можем записывать наше решение следующим образом : «1 вариант: первая полоса – красная, вторая – синяя, третья – белая.» и т.д. Но это очень долго и не удобно, записывая так, сложно сориентироваться все ли варианты мы записали, и не повторились ли мы где-нибудь. Поэтому очень удобно ввести кодирование, т.е. некоторое условное обозначение перебираемых в задаче объектов. В нашем случае мы заменим первой буквой каждый цвет полосы. Белый соответственно – «Б», красный – «К» и синий – «С». Введя кодирование, запись решения задачи очень упрощается. Мы имеем множество из трех элементов {Б, К, С}. Нужно составить различные комбинации из трех элементов, при этом порядок элементов учитывается. Например, запись «БКС» будет обозначать, что первая полоса флага – белая, вторая – красная, третья – синяя. Подобные задачи мы уже решали методом непосредственного перебора и построением дерева возможных вариантов. При встрече 8 приятелей обменялись рукопожатиями. Сколько всего было сделано рукопожатий? Данную задачу можно решать методом непосредственного перебора, и уже в самом начале заметим, что довольно сложно перебирать все возможные варианты и не запутаться, не говоря уже о записи решения этой задачи. Но, введя определенные обозначения - кодирование, решение будет очень легко представить Каждому приятелю даем номер от 1 до 8, а рукопожатия закодируем следующим образом: например число 24 означает что 2-ой приятель пожал руку 4-му. При чем число 35 и 53 означают одно и тоже рукопожатие, и брать будем меньшее из них. Коды рукопожатий мы можем оформить следующей таблицей: 12, 13, 14, 15, 16, 17, 18, 23, 24, 25, 26, 27, 28, 34, 35, 36, 37, 38, 45, 46, 47, 48, 56, 57, 58, 67, 68, 78. Таким образом, у нас получилось 1+2+3+4+5+6+7=28 рукопожатий. После того как учащиеся научились составлять всевозможные наборы, на первый план выдвигается задача подсчета числа возможных вариантов. Группа туристов планирует осуществить поход по маршруту Антоново – Борисово – Власово – Грибово. Из Антоново в Борисово можно сплавиться по реке или дойти пешком. Из Борисово во Власово можно пройти пешком или доехать на велосипедах. Из Власово в Грибово можно доплыть по реке, доехать на велосипедах или пройти пешком. Сколько всего вариантов похода могут выбрать туристы? Сколько вариантов похода могут выбрать туристы при условии, что хотя бы на одном из участков маршрута они должны использовать велосипеды? Построим для этой задачи дерево возможных вариантов: Пусть у нас «П»-обозначает путь пешком «Р» - сплавиться по реке «В» - доехать на велосипедах. 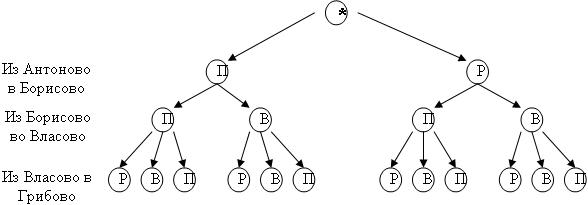 Ответ на второй вопрос также хорошо просматривается по дереву возможных вариантов. Но эту задачу можно решить по-другому, с помощью рассуждений. Из Антоново в Борисово у нас 2 варианта каким образом продолжать путь, из Борисово во Власово тоже 2 варианта, т.е. на каждый вариант первого участка пути у нас есть по 2 варианта второго участка пути и того на данном этапе у нас будет 2*2=4 варианта выбора способа передвижения. На каждый из этих 4 вариантов существует по 3 варианта способа передвижения по третьему участку пути из Власово в Грибово, т.е. 4*3=12. Ответ в этой задаче мы получили умножением. Еще одним способом подсчета комбинаторных наборов является использование правила суммы. Из класса нужно выделить одного дежурного, мальчика или девочку. Сколько существует способов для выбора дежурного, если в классе 22 девочки и 18 мальчиков? Выбрать одну девочку из 22 мы можем 22-мя способами, а одного мальчика из 18 можно 18-тью способами. Тогда выбрать одного дежурного мальчика или девочку можно (18+22) способами. Для подсчета вариантов мы использовали здесь правило суммы, которое можно сформулировать так: если два действия взаимно исключают друг друга, причем одно из них можно выполнить п способами, а другое – m способами, то какое-либо одно из них можно выполнить n+m способами. В нашем примере действия исключают друг друга, так как мы должны выбрать либо мальчика из одного множества, либо девочку из другого. В 6 классе продолжаем вероятностную линию. Начинаем с повторения, что такое случайное событие, определение его достоверности (невозможное, достоверное, маловероятное). Новой задачей становится формирование умения оценивать вероятности двух и более событий (более или менее вероятно). Полезно рассматривать задачи, в которых при ответе на вопросы необходимо опираться на свою интуицию. Можно рассматривать реальные жизненные ситуации, чтоб учащиеся видели непосредственную связь изучаемого с действительностью. Вы купили в магазине телевизор, на который фирма-производитель дает два года гарантии. Какие из следующих событий невозможные, случайные, достоверные: А) телевизор не сломается в течении года. Б) телевизор не сломается в течении двух лет. В) в течение двух лет вам не придется платить за ремонт телевизора. Г) телевизор сломается на третий год. Здесь нужно обратить внимание учащихся, что первые два события случайные, так как, во-первых, гарантия фирмы производителя вовсе не обозначает, что в течение двух лет телевизор будет работать идеально, а во-вторых, можно рассмотреть и тот случай, когда телевизор может сломаться по вине покупателя. Событие Г также является случайным, так как нельзя говорить, что телевизор обязательно сломается после того, как закончится срок гарантии. В 6 классе учащимся предлагается качественно новая деятельность для урока математики – проведение экспериментов. Это могут быть эксперименты с подбрасыванием кубика, монеты или кнопки. Все результаты экспериментов необходимо оформлять в виде таблиц, которые заполняются по ходу эксперимента. Для проведения экспериментов учащихся лучше разбить группы по 2-3 человека, один из которых будет фиксировать результаты эксперимента, а остальные проводить его. Могут быть предложены следующие задания-эксперименты. Задание №1. 100 раз подбросить монету и зафиксировать количество выпадений «орла» и «решки». Задание №2. 100 раз подбросить кнопку и зафиксировать количество раз, когда кнопка упала острием вниз и количество раз, когда кнопка упала острием вверх. Задание №3. Выберите какой-нибудь текст, содержащий 150 слов. Подсчитайте число слов, составленных из 6 букв. Задание №4. Выберите 7 строк произвольного текста (можно несколько различных текстов). Подсчитайте сколько раз встречаются в тексте буквы о, е, а, ю. Результатом должны быть таблицы примерно такого плана: Таблица №1. «Эксперимент по подбрасыванию монеты».
После проведения эксперимента, введем понятие частота и вероятность случайного события. Кроме экспериментов, рассматриваются задачи с уже известными данными о появлении некоторого события, и требуется вычислить вероятность этого события. Известно, что на 100 батареек попадаются 3 бракованные. Какова вероятность купить бракованную батарейку. В этой задаче необходимо вычислить вероятность события А: «купить бракованную батарейку», зная, что из ста случаев, это событие произошло 3 раза. Таким образом, получаем, что Р(А) = 0,03. Составляя таблицы с результатами, проведенных экспериментов, учащиеся приобретают навыки работы со статистическими данными (представление статистических данных и некоторые выводы из них). Кроме этого в 6 классе рассматриваются задачи непосредственно направленные на работу с таблицами (чтение и составление). Некоторые таблицы бывают очень простые (с ними мы работали в 5 классе), но бывают таблицы и по сложнее. Например, турнирные таблицы, в которых записывается ход соревнования и его результаты. Рассмотрим турнирную таблицу, в которой представлены итоги шахматного турнира с четырьмя участниками:
За победу участник получает 1 очко, за проигрыш – 0, а за ничью -1/2. По данной таблице могут быть заданы следующие вопросы: 1) сколько партий сыграл каждый участник 2) как сыграл Поликарпов с каждым из участников 3) заполнить последний столбец, сосчитав, сколько очков набрал каждый участник. 4) определить, используя данные в столбце «Очки», как распределились места между участниками. Заключение В данной дипломной работе была сделана попытка проанализировать возможность реализации стохастической линии в основной школе. Была проанализирована различная учебно-методическая литература по этой теме и на основе этого анализа сделаны конкретные выводы, с краткими методическими рекомендациями. На основе этих выводов разработана методика реализации стохастической линии в 5-6 классах, в каждом из которых рассматривается ведение всех направлений. Данная методическая разработка лишь один из вариантов реализации стохастической линии в курсе основной школы. По данной теме сейчас активно ведется работа по всем направлениям, так как на данный момент осталось еще не мало нерешенных проблем связанных с реализацией этой линии в основной школе. Данная работа может быть рекомендована для практического использования студентами-практикантами математического факультета и учителям математики. Этот материал может использоваться как на уроках, так и на факультативных и кружковых занятиях. Список литературы
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


