Конкурс научно-исследовательских работ «Академические чтения»
 Скачать 163.65 Kb. Скачать 163.65 Kb.
|
| Республиканский конкурс научно-исследовательских работ «Академические чтения» Секция математики им. Н.Г. Четаева Исследовательская работа Геометрические фракталы Уразова Диляра Зуфаровна, 7 класс Направляющая организация: МБОУ«Высокогорская средняя общеобразовательная школа № 2» Научный руководитель: учитель математики I категории Аксанова Ильсияр Исмагиловна Казань 2013 Содержание Введение………………………………………………………….…….3 Глава 1 § 1. Фракталы и их применение…………………………………….…4 § 2. Классификация фракталов…………………………………….…..7 Глава 2 § 1. Геометрический метод построения фракталов…………….…….9 § 2. Построение кривой Серпинского…………………………….…13 § 3. Построение фрактала «журавлиный клин»………………….….14 Глава 3 § 1. Метод построения фракталов с помощью L-кодов…………..…15 § 2. Примеры построения некоторых фрактальных кривых…….…16 §3. Построение кривой с помощью L-кодов…………………….…..19 Заключение…………………………………………………………….20 Список литературы…………………………………………………....20 Введение До недавнего времени геометрические модели различных природных конструкций традиционно строились на основе сравнительно простых геометрических фигур: прямых, многоугольников, окружностей, многогранников, сфер. Однако, очевидно, что этот классический набор, вполне достаточный для описания элементарных структур, становится плохо применимым для характеристики таких сложных объектов, как очертание береговых линий материков, поле скоростей в турбулентном потоке жидкости, разряд молнии в воздухе, пористые материалы, форма облаков, снежинки, пламя костра, контуры дерева, кровеносно-сосудистая система человека, поверхность клеточной мембраны и др. Для описания этих и им подобных образований ученые все чаще используют новые геометрические понятия. Одним из таких понятий, изменившим многие традиционные представления о геометрии, явилось понятие фрактала. Оно было введено в обращение замечательным французским математиком Бенуа Мандельбротом в 1975 году. Важную роль в широком распространении идей фрактальной геометрии сыграла замечательная книга Б.Мандельброта “Фрактальная геометрия природы”. Основой фрактальной геометрии является идея самоподобия. Она выражает собой тот факт, что иерархический принцип организации фрактальных структур не претерпевает значительных изменений при рассмотрении их через микроскоп с различным увеличением. В результате эти структуры на малых масштабах выглядят в среднем также как и на больших. История развития идей фрактальной геометрии тесно связана с именами таких известных математиков, как Вейерштрасс, Кантор, Пеано, Хаусдорф, Безикович, Кох, Серпинский и др. Хаусдорф в 1919 г. ввел понятие о дробной (фрактальной) размерности множеств и привел первые примеры таких множеств. Среди них были канторовское множество, кривая Коха и другие экзотические объекты, мало в то время известные за пределами чистой математики. Цели данной исследовательской работы:
В данной исследовательской работе нами были изучены понятие фрактала, примеры фракталов, их классификация и применение в различных областях науки и жизни. Изучены геометрический метод построения геометрических фракталов и метод построения с помощью L-кодов. Геометрическим методом были построены кривая Серпинского и фрактал «журавлиный клин». С помощью метода L-кодов были построены фрактал «прямоугольник» и фрактал «солнышко». Глава 1. § 1. Фракталы и их применение Фракталами называются геометрические объекты: линии, поверхности, пространственные тела, имеющие сильно изрезанную форму и обладающие свойством самоподобия. Слово фрактал произошло от латинского слова fractus и переводится как дробный, ломаный. Самоподобие как основная характеристика фрактала означает, что он более или менее единообразно устроен в широком диапазоне масштабов. Так, при увеличении маленькие фрагменты фрактала получаются очень похожими на большие. В идеальном случае такое самоподобие приводит к тому, что фрактальный объект не изменяет основных своих геометрических особенностей при изменении масштаба. Фракталы находят все большее и большее применение в науке. Основная причина заключается в том, что они описывают реальный мир иногда даже лучше, чем традиционная физика или математика. Мы можем наблюдать фракталы в природе: модель горного хребта, крона дерева, листья папоротника, река и ее притоки, языки пламени, система кровообращения, дыхательная система и легкие, почки, каскадные водопады, гроза, облака, тучи, турбулентные процессы. 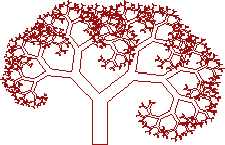    Приведем несколько примеров применения фракталов. Компьютерные системы. Наиболее полезным использованием фракталов в компьютерной науке является фрактальное сжатие данных. В основе этого вида сжатия лежит тот факт, что реальный мир хорошо описывается фрактальной геометрией. При этом, картинки сжимаются гораздо лучше, чем это делается обычными методами (такими как jpeg или gif). Другое преимущество фрактального сжатия в том, что при увеличении картинки, не наблюдается эффекта пикселизации (увеличения размеров точек до размеров, искажающих изображение). При фрактальном же сжатии, после увеличения, картинка часто выглядит даже лучше, чем до него. Механика жидкостей. Изучение турбулентности в потоках очень хорошо подстраивается под фракталы. Турбулентные потоки хаотичны и поэтому их сложно точно смоделировать. И здесь помогает переход к их фрактальному представлению, что сильно облегчает работу инженерам и физикам, позволяя им лучше понять динамику сложных потоков. При помощи фракталов также можно смоделировать языки пламени. Пористые материалы хорошо представляются в фрактальной форме в связи с тем, что они имеют очень сложную геометрию. Это используется в нефтяной науке. Текоммуникации. Для передачи данных на расстояния используются антенны, имеющие фрактальные формы, что сильно уменьшает их размеры и вес. Физика поверхностей. Фракталы используются для описания кривизны поверхностей. Неровная поверхность характеризуется комбинацией из двух разных фракталов. Медицина. Биосенсорные взаимодействия, биения сердца, нервная и кровеносная системы млекопитающих Биология. Моделирование хаотических процессов, в частности при описании моделей популяций. Литература. Среди литературных произведений находят такие, которые обладают текстуальной, структурной или семантической фрактальной природой. В текстуальных фракталах потенциально бесконечно повторяются элементы текста: неразветвляющееся бесконечное дерево, тождественное самой себе с любой итерацией («У попа была собака…», «Притча о философе, которому снится, что он бабочка, которой снится, что она философ, которому снится…», «Ложно утверждение, что истинно утверждение, что ложно утверждение…») Язык фрактальной геометрии необходим, например, при изучении поглощения или рассеяния излучения в пористых средах, для характеристики сильно развитой турбулентности, при моделировании свойств поверхности твердых тел, для описания молнии, при анализе процессов усталостного разрушения материалов, при исследовании различных стадий роста вещества за счет диффузии и последующей агрегации, в квантовой механике. Удивительно то, что сходные геометрические формы встречаются в совершенно различных областях науки: в астрономии при описании процессов образования галактик во Вселенной, в картографии при изучении форм береговых линий и разветвленной сети речных русел и, например, в биологии, при анализе строения кровеносной системы или рассмотрении сложных поверхностей клеточных мембран. Мир фракталов многообразен. Для того чтобы представить все многообразие фракталов удобно прибегнуть к их общепринятой классификации. § 2. Классификация фракталов Все разнообразие фракталов можно разделить на три больших класса:
Геометрические фракталы.Первыми были открыты так называемые детерминированные фракталы. Их отличительной чертой является свойство самоподобия, обусловленное особенностями метода их генерации. Некоторые предпочитают называть эти фракталы классическими, геометрическими фракталами или линейными фракталами.Фракталы этого класса самые наглядные. Эти фракталы обычно формируются, начиная с инициатора — фигуры, к которой применяется определенный основной рисунок. Во всех геометрических фракталах самоподобие проявляется на всех уровнях то есть независимо от того насколько вы приближаете фрактал, вы увидите все тот же узор. Для сложных фракталов, которые будут рассмотрены позже, это не так. Ниже находятся примеры некоторых геометрических фракталов.   Снежинка Коха Шестиугольник Серпинского   Квадратный ковер Серпинского Губка Менгера Алгебраические фракталы Это самая крупная группа фракталов. Получают их с помощью нелинейных процессов в n-мерных пространствах. Наиболее изучены двумерные процессы. Интерпретируя нелинейный итерационный процесс, как дискретную динамическую систему, можно пользоваться терминологией теории этих систем: фазовый портрет, установившийся процесс, аттрактор и т.д.  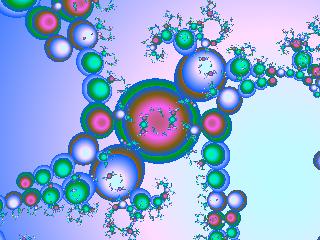 Стохастические фракталы Еще одним известным классом фракталов являются стохастические фракталы, которые получаются в том случае, если в итерационном процессе случайным образом менять какие-либо его параметры. При этом возникают объекты очень похожие на природные – несимметрические деревья, изрезанные береговые линии и т.д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря. Существуют и другие классификации фракталов, например деление фракталов на детерминированные (алгебраические и геометрические) и недетерминированные (стохастические).  Глава 2. §1. Геометрический метод построения фракталов История фракталов началась с геометрических фракталов, которые исследовались математиками еще в XIX веке. Многие называют эти фракталы классическими или линейными. Фракталы этого класса — самые наглядные, потому что в них сразу видно самоподобие. Эти фракталы обычно формируются, начиная с инициатора — фигуры, к которой применяется определенный основной рисунок. Во всех геометрических фракталах самоподобие проявляется на всех уровнях. Это значит, что независимо от того, насколько вы приближаете фрактал, узор будет тем же. Геометрические фракталы образуются в процессе, называемом итерацией, которая применяет основной рисунок к инициатору, после чего применяет его к результату и так далее. Большинство людей итерируют геометрические фракталы 5-7 раз, чтобы получить четкую красивую картинку. Для сложных фракталов это не так. Одномерные геометрические фракталы линейны, так как при каждой итерации что-то убирается, либо прибавляется в форме прямых линий. Такие фракталы можно получить, задав некоторую ломаную (или поверхность в трехмерном случае), называемую генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор в соответствующем масштабе. В результате бесконечного повторения этой процедуры получается геометрический фрактал. Рассмотрим несколько примеров построения геометрических фракталов. Пример 1.Построение кривой Коха. Для построения этой кривой выполняем следующие действия (рис.1): 1. Единичный отрезок делим на три равные части. 2. Отбрасываем среднюю часть. 3. На месте средней части строим как на основании, равносторонний треугольник. 4. Повторяем процедуру с каждым из построенных отрезков. 5. Выполняем любое конечное число итераций. Мы в своей работе построили пять итераций кривой Коха. 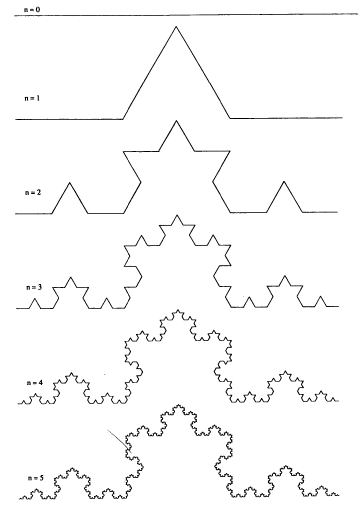 Рис.1. Построение кривой Коха. Если в качестве исходного объекта выбрать не единичный отрезок прямой, а равносторонний треугольник со сторонами единичной длины, то с помощью той же процедуры возникает симметричная, похожая на снежинку, бесконечно изломанная кривая, которая представляет собой самоподобное множество, называемое снежинкой Коха (рис.2). Она была так названа в честь шведского математика Helge von Koch, который впервые описал ее в 1904 году. Отличительной ее особенностью является то, что она, будучи замкнутой, тем не менее нигде себя не пересекает, поскольку достраиваемые треугольники каждый раз достаточно малы и никогда не «сталкиваются» друг с другом. В качестве нулевой итерации рассматривается равносторонний треугольник: 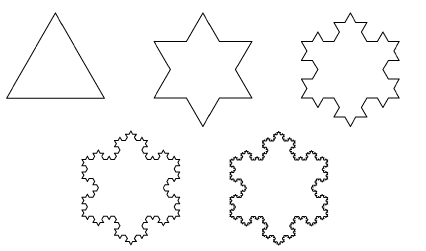 Рис.2. Построение снежинки Коха Пример 2. Построение ковра Серпинского. Геометрический фрактал, называемый ковром Серпинского, получается последовательным вырезанием центральных равносторонних треугольников следующим образом (рис.3): 1. Берем равносторонний треугольник со сторонами единичной длины 2. Проводим прямые, соединяющие попарно середины сторон 4. Получим 4 треугольника. Отбросим центральный треугольник 5. С каждым из 3-х оставшихся треугольников проделаем те же операции. После бесконечного повторения итераций мы получим предельное множество, которое называется ковром Серпинского .  Рис.3. Построение ковра Серпинского. § 2. Построение кривой Серпинского. Можно построить непрерывную линию, геометрически эквивалентную ковру Серпинского. Инициирующим элементом для такого построения берется отрезок единичной длины, который потом заменяется на конструкцию, называемую генератором, состоящую из трех отрезков длиной 1/2 , расположенных под углом 120 градусов друг к другу. Затем каждый из этих отрезков заменяется, в свою очередь, на генератор в два раза меньшего размера так, как показано на рис.4.
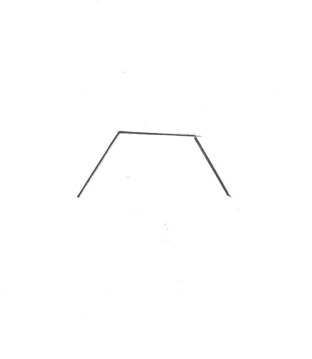
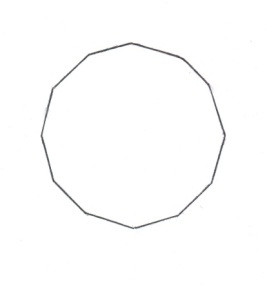
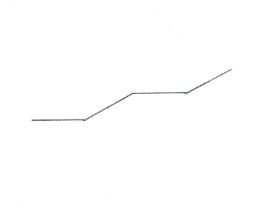
Рис.4. Построение кривой Серпинского. Контуры будущего ковра Серпинского отчетливо проступают на следующих двух этапах (рис.5). Эта процедура повторяется до бесконечности. Легко видеть, что каждое следующее изображение может быть получено из предыдущего путем склеивания трех уменьшенных в два раза его копий, две из которых повернуты на угол в 120 и -120 градусов относительно оригинала. 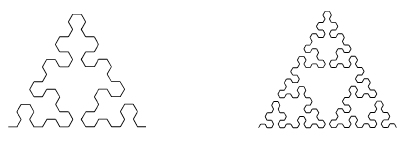 Рис.5. Следующие два шага в построении кривой Серпинского. § 3. Построение фрактала «журавлиный клин» Алгоритм построения фрактала «журавлиный клин»: 1. Берем квадрат со стороной единичной длины 2. Делим исходный квадрат на 16 равных квадратов со стороной ¼ 3. Отбросим не закрашенные 9 квадратов 4. С каждым из оставшихся 7 закрашенных квадратов проделываем ту же процедуру Процедуру повторяем сколько угодно раз. На рис.6. представлено 5 итераций. 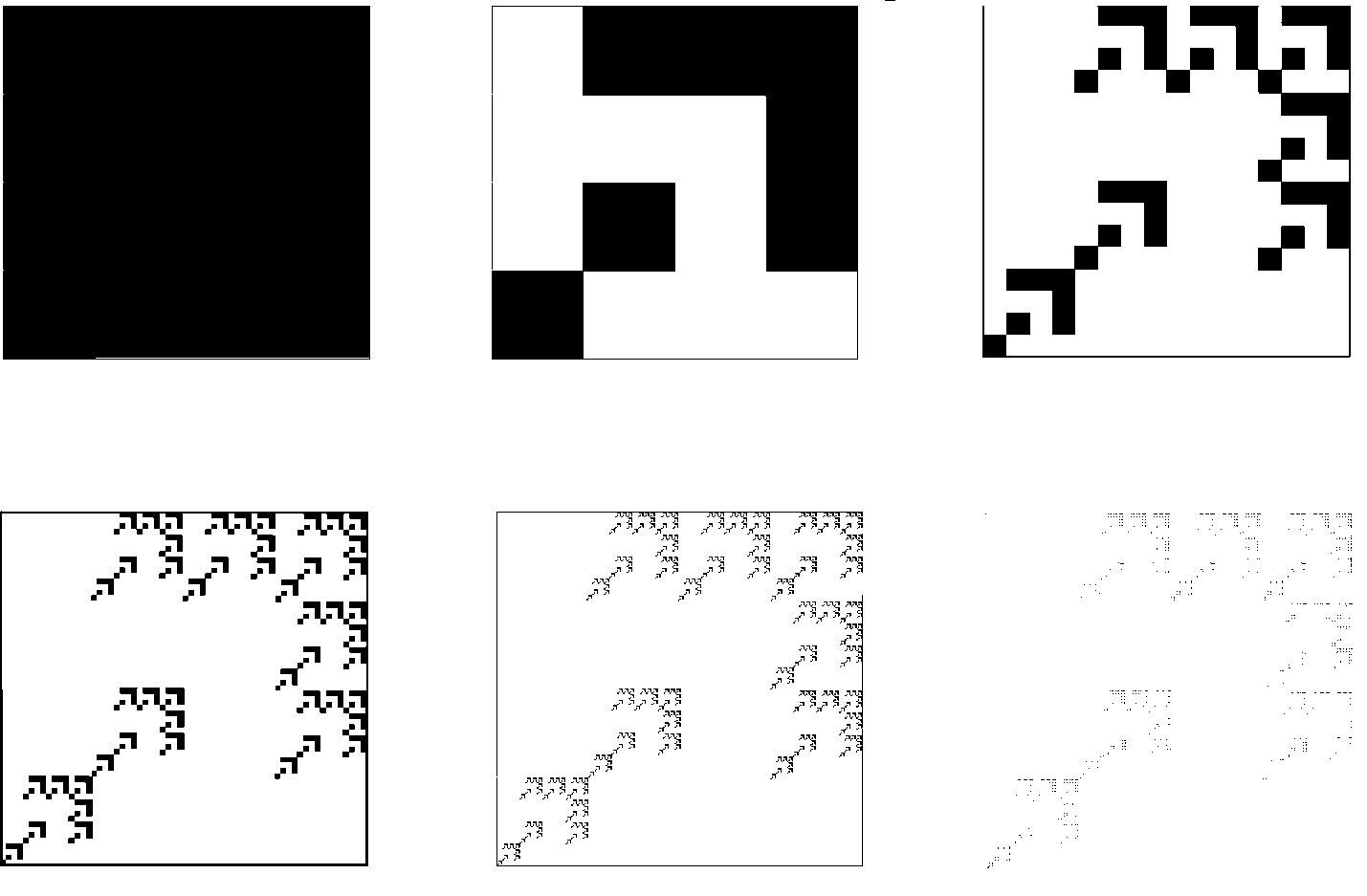 Рис.6. Построение фрактала «журавлиный клин» Глава 3. § 1. Метод построения фракталов с помощью L-кодов. Напомним, что фрактальной кривой называется кривая, состоящая из частей, каждая из которых представляет уменьшенную копию целого. В самом простом случае небольшая часть фрактальной кривой содержит информацию о всей кривой. Большинство фрактальных кривых имеет интересную и сложную структуру. Для построения таких кривых существуют различные способы, одним из которых является метод L-кодов. Это наиболее простой способ построения геометрических фракталов, разработанный в 1968 году Аристидом Линденмайером. Он был биологом по образованию и изначально рассматривал L-системы, как формальный способ описания развития биологических объектов, но позже L-системы нашли применение в компьютерной графике. Оказалось, что с их помощью очень удобно рисовать фракталы и различные природные объекты с самоподобной структурой. Метод построения графических объектов с помощью L-кодов ещё называют "черепашьей графикой" (turtle geometry). В алгоритме построения фрактальных кривых используется код для описания кривой. Простейший код состоит из буквы Е и знаков + и - . Кроме этого, задаются два угла φ и φ0. Буква Е означает, что мы чертим отрезок длины l в нужном нам направлении. Знак + означает, что следующий отрезок мы будем чертить в направлении на угол φ против часовой стрелки, и знак - означает, что поворот происходит на угол φ по часовой стрелке. Угол φ0 задает начальное направление. Если дана координатная система XOY, то φ0 – начальный угол между осью OX и первым отрезком Е. Угол φ0 откладывается от положительного направления оси OX против часовой стрелки. §2. Примеры построения некоторых фрактальных кривых методом L-кодов. Пример1. На рис.7. а). Простой код Е, состоящий только из одной буквы Е и угла φ0 = 0, задает отрезок, параллельный оси OX. б). Простой код Е, состоящий из одной буквы Е и угла φ0 = π/2, задает отрезок, параллельный оси OY. в). Код Е-Е с углами φ0 =0 и φ = π/2 задает ломаную линию. Сначала откладываем отрезок длины l в положительном направлении оси OX, потом поворачиваем по часовой стрелке на φ = π/2 и откладываем отрезок длины l в отрицательном направлении оси OY. 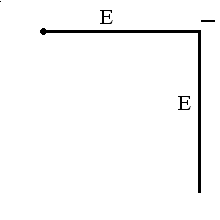 Рис.7 Пример 2. Возьмем φ0 = 0 и φ = π/2 и построим кривую с помощью кода Е+Е+Е+Е. Мы начинаем двигаться в положительном направлении оси OX. Первая буква Е означает, что мы передвигаемся на l единиц в этом направлении. Знак + после Е означает, что мы изменяем направление на π/2 так, что оно совпадает с положительным направлением оси OY. Третий знак кода, буква Е, означает, что мы передвигаемся вверх на l единиц. Четвертый знак кода + означает, что мы снова поворачиваем на угол π/2, и направление изменяется на отрицательное направление оси OX. Пятый знак кода, буква Е, означает, что мы передвигаемся на l единиц в этом направлении. Следующий знак + меняет данное направление на отрицательное направление оси OY, и последняя буква Е в коде означает, что мы двигаемся вниз на l единиц. В итоге мы придем в ту же самую точку, откуда начали построение. Таким образом, мы построили заданную L-кодом кривую, и в результате получился квадрат (рис.8). 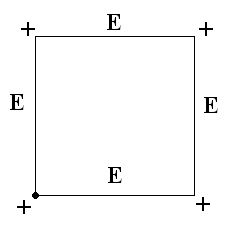 Рис.8 Пример 4. Построение кривой Коха с помощью L-кода. Рассмотрим кривую, порожденную кодом Е+Е- -Е+Е, где углы φ0 = 0 и φ = π/3. Сначала мы перемещаемся вправо на l единиц, затем изменяем направление на угол π/3 против часовой стрелки и снова передвигаемся на l единиц. Два знака - означают, что теперь мы меняем направление на отрицательный угол -2π/3 и получаем направление, образованное углом -π/3 и положительным направлением оси ох. Мы передвигаемся на l единиц, и последний знак + означает, что мы меняем данное направление на положительное направление оси ох, и передвигаемся на l единиц в конец кривой (рис.9). Заметим, что конечная точка находится на расстоянии 3l вправо от начальной точки. 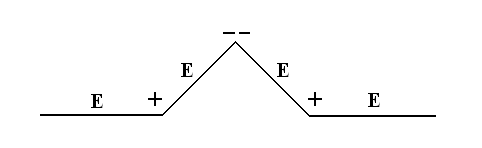 Рис.9 Кривые, представленные в примерах 1-4, не являются очень сложными. Для получения более сложных кривых используем правило подстановки. Для этого букву Е будем заменять на заданную последовательность кода в любом месте, где она встретится в этой последовательности. Повторяя эту замену много раз, мы будем получать все более сложные кривые, и в предельном случае получим действительно сложную фрактальную кривую. Заметим, что начальный код кривой и код подстановки могут не совпадать. В процессе выполнения этой замены мы видим, что начальная точка кривой после подстановки остается той же, что и у первоначальной кривой (аналогично и для конечной точки) Таким образом, мы изменяем длину l в значении буквы Е на каждом шаге замены. Пример 5. Пусть кривая порождается простым кодом Е и φ0 =0 и φ = π/3. Возьмем замену кода Е+Е- -Е+Е. На первом этапе мы получим только одну линию, а после первой замены - кривую из примера 4. После второй замены мы получим код Е+Е- -Е+Е + Е+Е- -Е+Е - - Е+Е- - Е+Е + Е+Е- -Е+Е. Изображая соответствующую кривую, мы заменим любой отрезок в кривой из примера 4 на копию, которая будет в три раза меньше исходной кривой (рис.10). 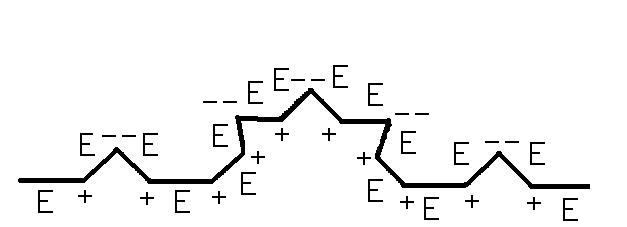 Рис.10 Повторяя эту процедуру, мы в предельном варианте получим кривую Коха. Если изменить простой начальный код в примере 5 на Е- -Е- -Е и взять те же углы и ту же замену кода, то таким образом мы получим снежинку Коха (рис.11).  Рис.11 § 3. Построение кривой с помощью L-кодов Задача 1. Возьмем кривую, полученную с помощью кода ЕЕ+Е+ЕЕ+Е, где углы φ0 = 0 и φ = π/2. Отличие от кривой в примере 2 состоит в том, что мы теперь перемещаемся на 2l единиц в направлении, параллельном оси OX, и кривая будет прямоугольником, горизонтальные стороны которого в два раза больше вертикальных сторон (рис.12). 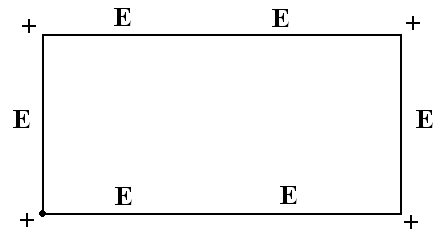 Рис.12 Задача 2. Построить кривую с начальным кодом Е-Е-Е-Е-Е-Е-Е-Е-Е-Е-Е-Е-Е, где φ0 = 0 и φ = π/6 и заменой Е+Е-Е+Е. Сначала строим кривую по начальному коду и получаем правильный 12-ти угольник. Затем строим кривую замены. Делаем замену и получаем первую итерацию фрактала «солнышко» (рис. 13)
Рис.13. Построение фрактала «солнышко» Заключение В представленной исследовательской работе мы познакомились с увлекательнейшим и многообразным миром фракталов. В работе нами изучены понятие фрактала, описана классификация фракталов, применение фракталов в различных областях прикладных наук. Рассмотрены и изучены два способа построения фракталов: геометрический и способ построения с помощью L-кодов. Приведенные в работе примеры дают достаточно четкое понимание алгоритма построения фракталов. Геометрическим методом были построены кривая Серпинского и фрактал «журавлиный клин». С помощью метода L-кодов были построены фрактал «прямоугольник» и фрактал «солнышко». В заключение хочется сказать, что тема эта меня очень увлекла, и я думаю, в дальнейшем буду продолжать изучение фракталов и еще один способ построения геометрических фракталов с помощью систем итерируемых функций. Список литературы.
|