|
Элективный курс для 9 класса Автор программы: Малахова А. А. учитель математики 2010 2011 учебный год, с. Юрловка
Юрловский филиал
МОУ «Никифоровская СОШ №2»
Избранные вопросы
математики
элективный курс для 9 класса
Автор программы:
Малахова А.А.
учитель математики
2010 – 2011 учебный год,
с. Юрловка
Аннотация
В связи с введением в 9 классе государственной итоговой аттестации в новой форме возникла необходимость в обеспечении интенсивного повторения школьного курса математики и подготовки учащихся к продолжению образования.
Умение решать задачи на проценты, линейные и квадратные уравнения и неравенства, иррациональные уравнения определенного уровня сложности, системы уравнений и неравенств, прогрессии является обязательным требованием, предъявляемым к выпускникам основной школы.
Цель элективного курса состоит в повышении уровня математической культуры и компетентностей учащихся, в развитии логичности и конструктивности мышления.
Основные задачи элективного курса:
развитие математического интереса, интеллектуальное и творческое развитие учащихся;
формирование математической грамотности;
обеспечить условия для самостоятельной творческой работы.
Содержание программы курса
№
|
Тема
|
Краткое содержание
|
1.
|
Преобразование рациональных выражений
|
Повторить определение рациональных выражений, сформулировать основные правила преобразования рациональных выражений. Закрепить полученные навыки.
|
2.
|
Способы решения алгебраических уравнений.
|
Рассмотреть способы решения алгебраических уравнений. Закрепить полученные навыки при решении уравнений.
|
3.
|
Решение алгебраических неравенств.
|
Рассмотреть простейшие решения неравенств. Закрепить полученные навыки при решении неравенств.
|
4.
|
Иррациональные уравнения
|
Рассмотреть уравнения вида 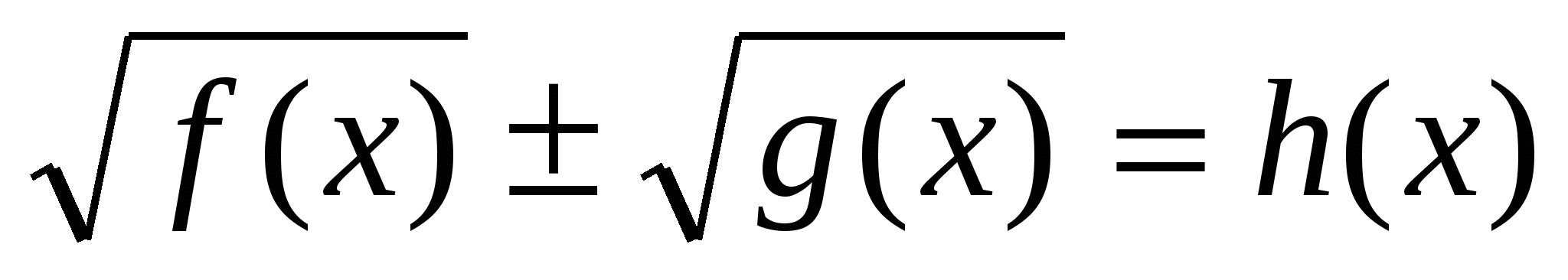 и способы их решения. Закрепить полученные навыки при решении уравнений. и способы их решения. Закрепить полученные навыки при решении уравнений.
|
5.
|
Методы решения систем уравнений и неравенств
|
Рассмотреть способы решения систем уравнений и неравенств. Закрепить полученные навыки при решении
|
6.
|
Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины.
|
Рассмотреть приемы раскрытия знака модуля. Рассмотреть уравнения вида 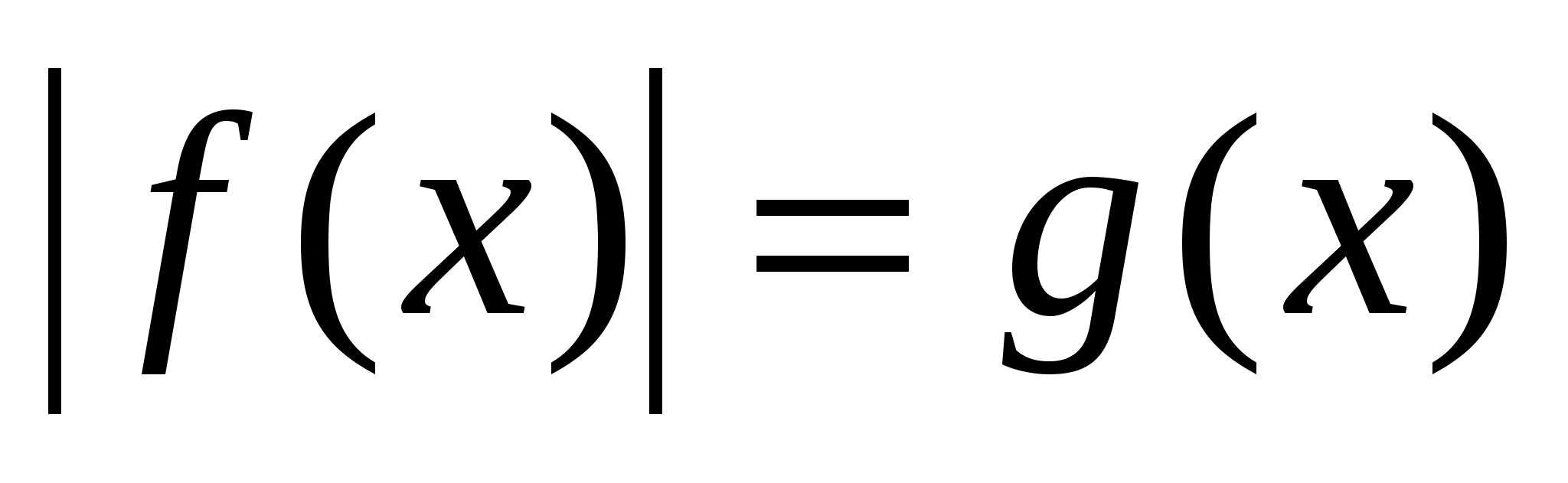 , , 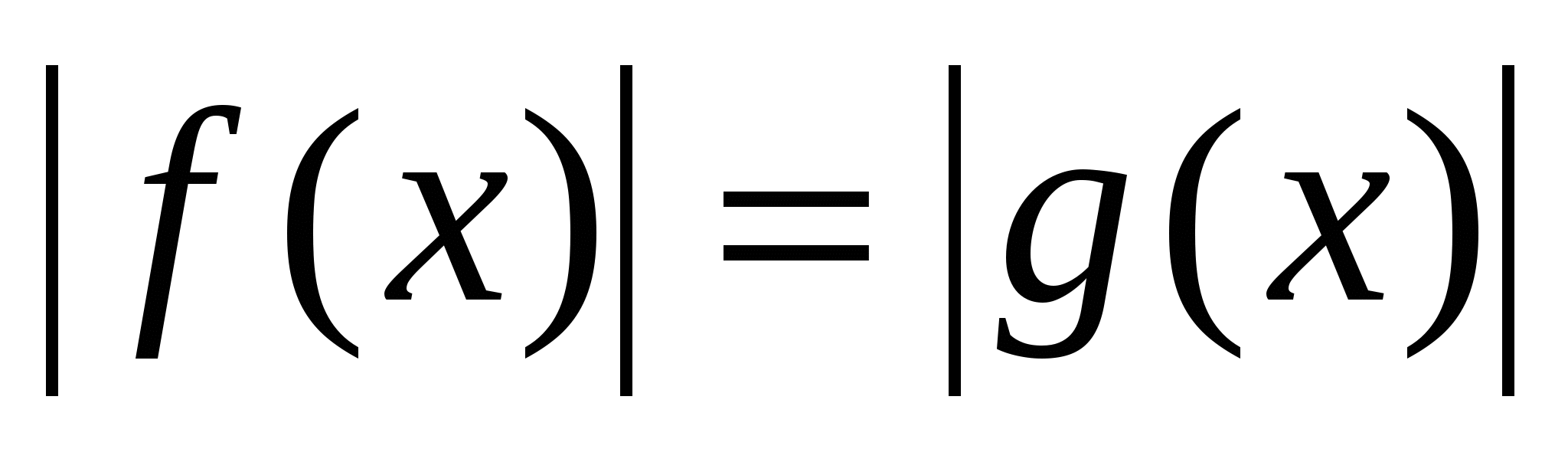 неравенства вида неравенства вида 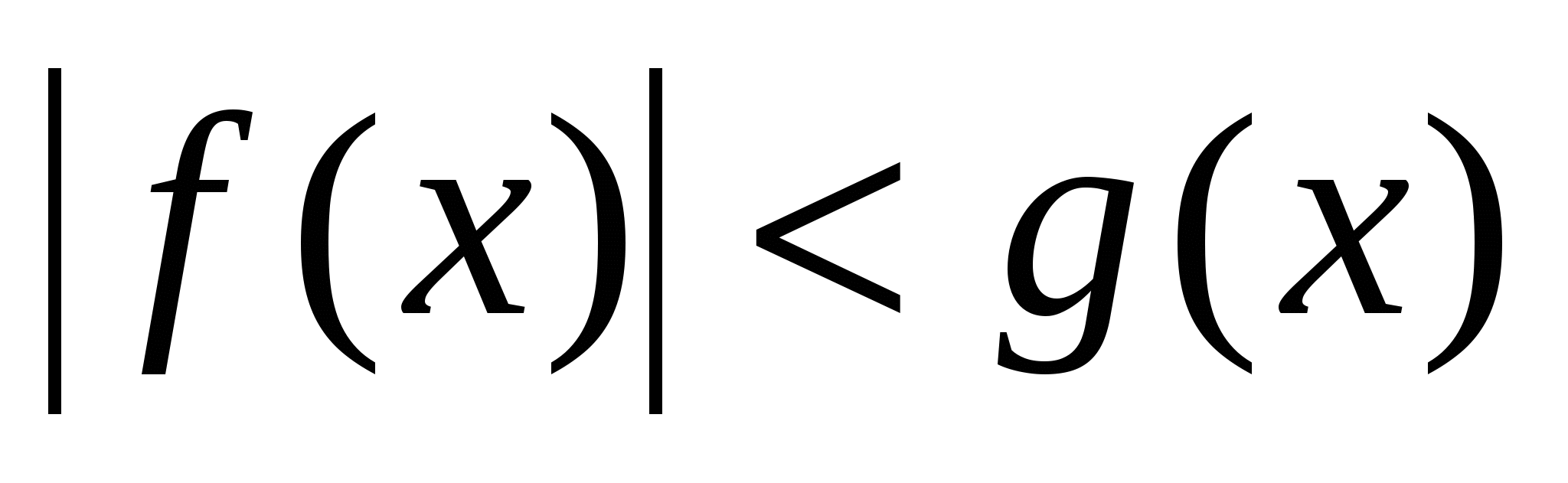 , , 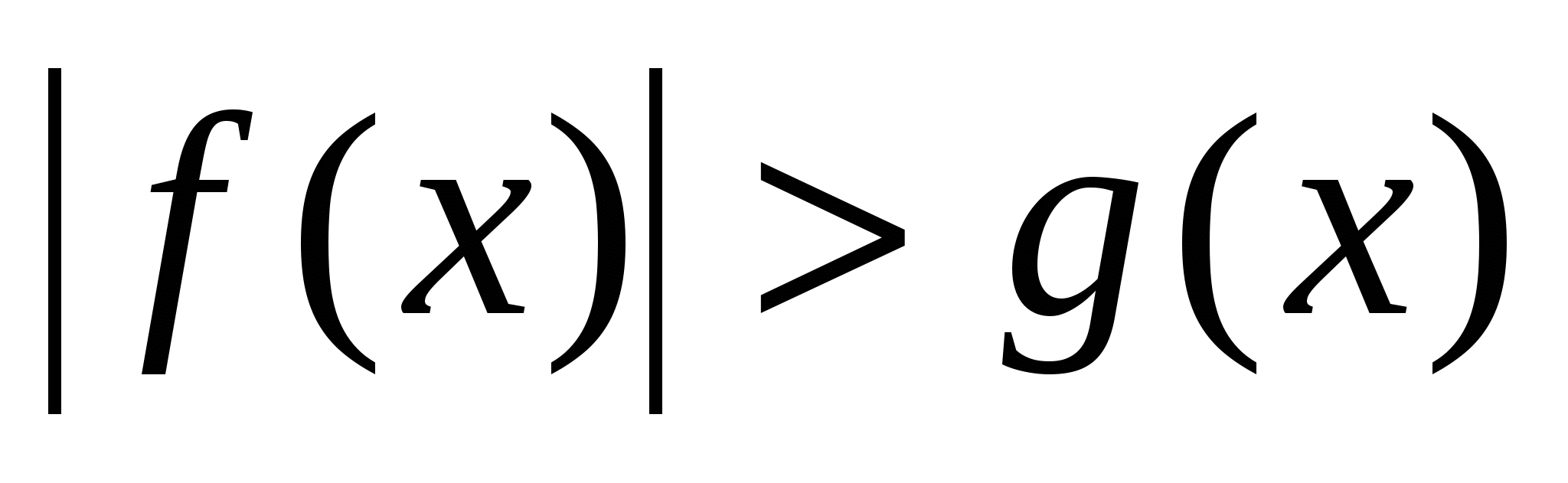 , , 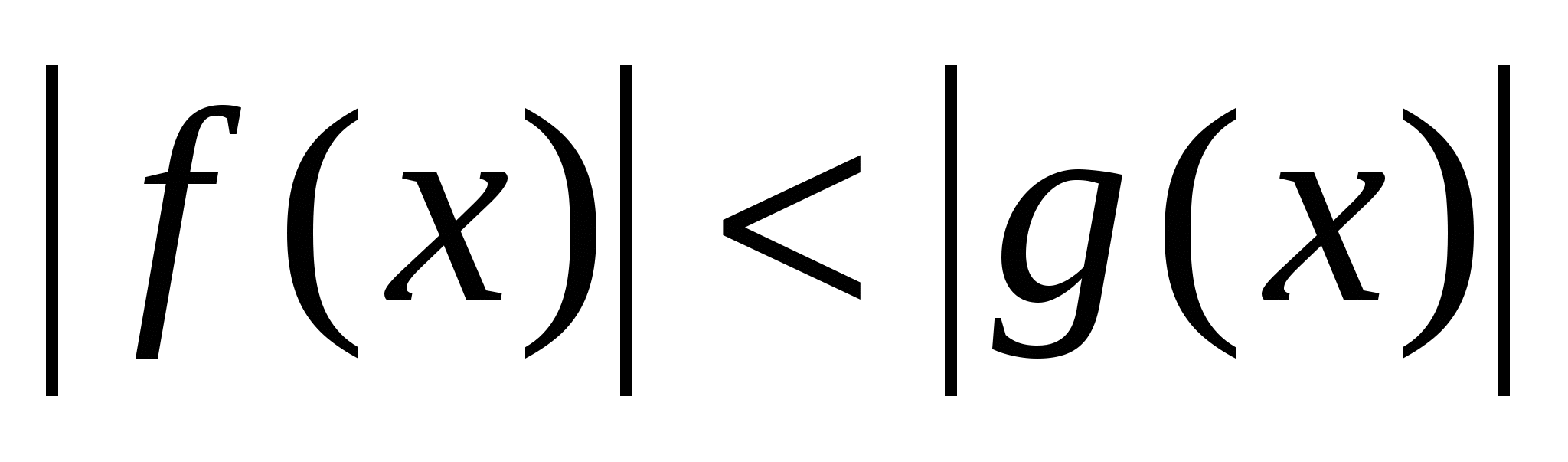 , , 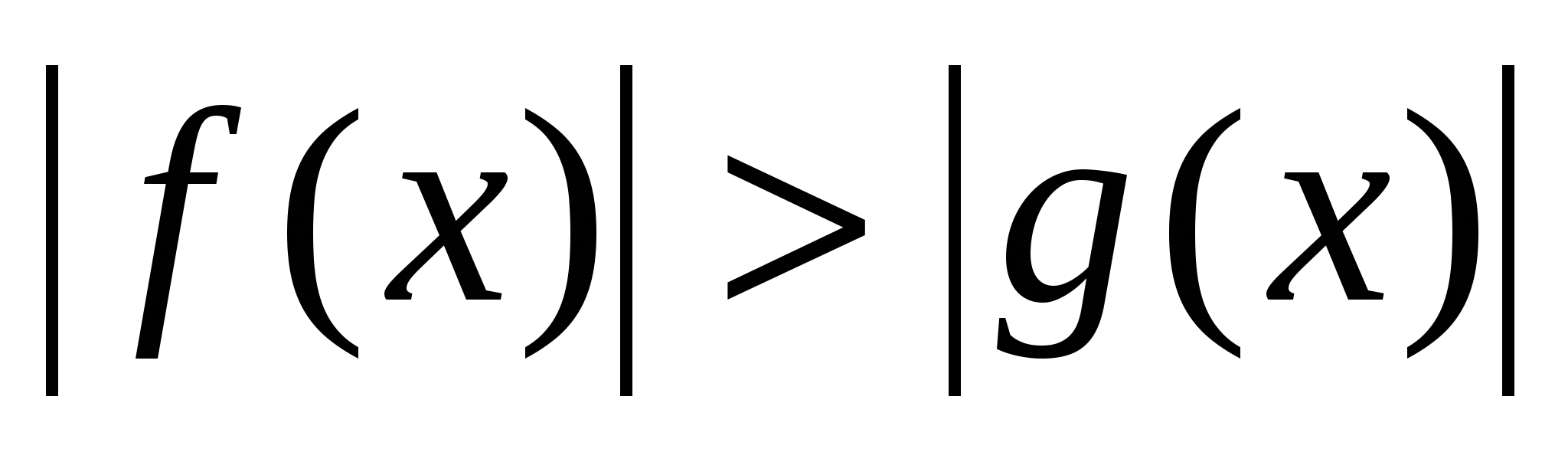 и способы их решения. Закрепить полученные навыки при решении уравнений и неравенств. и способы их решения. Закрепить полученные навыки при решении уравнений и неравенств.
|
7.
|
Прогрессии.
|
Ввести математическую модель – числовая последовательность. Дать определение прогрессии, формул п-го члена, характеристического свойства и формул суммы п членов. Закрепить полученные навыки при решении задач.
|
8.
|
Решение текстовых задач.
|
Рассмотреть приемы решений задач на движение, смеси и сплавы, совместную работу, проценты. Закрепить полученные навыки при решении задач.
|
Учебно-тематическое планирование:
№
|
Тема занятия
|
Количество часов
|
Форма контроля
|
Всего
|
Лекция
|
Практикум
|
1.
|
Преобразование рациональных выражений
|
4
|
1
|
3
|
Домашняя контр. р.
|
2.
|
Способы решения алгебраических уравнений.
|
5
|
1
|
4
|
Самоконтроль по готовому решению, домашняя контр. работа.
|
3.
|
Решение алгебраических неравенств.
|
5
|
1
|
4
|
Самоконтроль по готовому решению, домашняя контр. работа.
|
4.
|
Иррациональные уравнения
|
2
|
1
|
1
|
Самоконтроль по готовому решению.
|
5.
|
Методы решения систем уравнений и неравенств
|
5
|
1
|
4
|
Взаимоконтроль по готовому решению, домашняя контр. работа.
|
6.
|
Уравнения и неравенства, содержащие неизвестную под знаком абсолютной величины.
|
3
|
1
|
2
|
Домашняя контр. р.
|
7.
|
Прогрессии.
|
4
|
1
|
3
|
Самостоятельная работа.
|
8.
|
Решение текстовых задач.
|
6
|
2
|
4
|
Самоконтроль по готовому решению, домашняя контр. работа.
|
Итого:
|
34
|
9
|
25
|
| Методические рекомендации
Занятия рекомендуется проводить в форме лекций и практикумов с использованием активных методов обучения (поисковых, исследовательских, игровых). Основная часть времени на каждом практическом занятии должна отводиться самостоятельной работе учащихся по индивидуальным карточкам с последующей проверкой правильности выполнения заданий, осуществляемой как путем самоконтроля по карточкам с ответами, так и со стороны учителя. Возможна так же комбинация индивидуальной работы и парной. Парный вид деятельности можно рекомендовать на этапе проверки правильности выполнения заданий, в ходе которого учащиеся обмениваются выполненными работами для их проверки друг у друга, после чего получают карточки с верными ответами для самоконтроля.
Данный курс предполагает использование тестовых домашних заданий для учащихся, желающих совершенствовать свои знания и умения.
В ходе практических занятий учитель руководит деятельностью учащихся, оказывает им помощь в случае необходимости, консультирует.
Требования к уровню подготовки учащихся
знать правила и уметь выполнять действия с целыми числами, дробями, квадратными корнями;
уметь применять формулы сокращённого умножения;
решать основные задачи на дроби, проценты;
выполнять действия со степенями с натуральными, целым и рациональными множителями;
уметь преобразовывать буквенные выражения;
уметь решать линейные и квадратные уравнения, несложные дробно-рациональные уравнения, применять в простейших случаях замену переменной;
уметь решать системы уравнений с двумя переменными (линейные и системы, в которых одно уравнение второй степени);
решать линейные неравенства с одной переменной и их системы, квадратные и сводимые к ним дробно-рациональные неравенства с одной переменной;
решать основные задачи на движение или, работу, задачи на проценты, концентрацию, части, доли, смеси;
уметь решать задачи на арифметическую и геометрическую прогрессии с применением формул nго члена прогрессии, либо формулы суммы n-первых членов прогрессии;
строить графики изученных функций, и отвечать на вопросы, связанные с их исследованием;
решать задачи геометрического содержания на координатной плоскости с использованием алгебраического метода и с опорой на графические представления;
знать определение модуля числа, свойства и уметь применять их при решении простейших задач;
уметь решать простейшие линейные и квадратные уравнения и неравенства, их системы с параметром.
Список литературы
Кузнецова Л.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра: сб. заданий для подготовки к итоговой аттестации в 9 кл. – М.: Просвещение, 2010.
Ковалева Г.И., Дюмина Т.Ю. Математика. 9 класс: сб. заданий с ответами – Волгоград: Учитель, 2010.
Минаева С.С., Колесникова Т.В. Математика. 9 класс. Государственная итоговая аттестация (по новой форме). Типовые тестовые задания. – М.: Экзамен, 2010.
Справочник по алгебре для школьников и абитуриентов. – М.: ООО «Агенство «КРПА Олимп»: ООО «Издательство «Астрель»: ООО «Издательство АСТ», 2002.
Гусев В.А., Мордкович А.Г. Математика: Алгебра: Геометрия: Прил.: Справ. материалы: Учебное пособие для учащихся. – М.: Просвещение, 1986.
Олехник С. Н., Потапов М. К., Пасиченко П. И. Уравнения и неравенства. Нестандартные методы решения. – М.: Дрофа, 2001.
Олехник С.Н., Потапов М.К., Пасиченко П.И. Уравнения и неравенства. Нестандартные методы решения. – М.: Дрофа, 2001.
Мордовина Е.Е. Исследование корней трехчлена второй степени с параметром. Учебное пособие. – Тамбов, 2002.
Интернет-ресурсы:
www.resolventa.ru - Учебно-методическое пособие для подготовки к ЕГЭ и ГИА
www.alekslarin.narod.ru – Диагностические и тренировочные работы, демоверсии ГИА
https://alleng.ru - Книги по подготовке к ЕГЭ и ГИА по различным предметам
http://www.kokch.kts.ru/cdo/ - Тестирование online: 5 - 11 классы
https://eqworld.ipmnet.ru - Мир математических уравнений
https://video-repetitor.ru/index.php/2009-12-15-13-44-17 - видеорепетитор
 |
|
|
 Скачать 87.6 Kb.
Скачать 87.6 Kb.