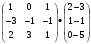Вопросы к экзамену по дисциплине «Элементы высшей математики»
 Скачать 42.25 Kb. Скачать 42.25 Kb.
|
| Вопросы к экзамену по дисциплине «Элементы высшей математики» 1.Матрицы, действия над матрицами. 2.Виды матриц. 3.Элементарные преобразования матриц. 4. Определитель. Его свойства. 5. Определитель. Вычисление определителя. 6.Обратная матрица. Алгоритм нахождения обратной матрицы. 7.Ранг матрицы. Алгоритм вычисления ранга матрицы с помощью элементарных преобразований. 8.Система линейных уравнений. Метод обратной матрицы. Формулы Крамера. Метод Гаусса. 9. Определение комплексного числа в алгебраической форме. Действия над комплексными числами в алгебраической форме. 10. Определение комплексного числа в тригонометрической форме. Действия над комплексными числами в тригонометрической форме. 11. Определение комплексного числа в показательной форме. Представление комплексного числа на плоскости. 12.Предел функции в точке. Основные теоремы о пределах. 13.Предел функции при х стремящемся к бесконечности. Замечательные пределы. Число е. 14.Непрерывность функции в точке и на промежутке. Точки разрыва функции. 15.Приращение аргумента. Приращение функции. Производная функции. Дифференциал функции. Геометрический смысл производной. Механический смысл производной. 16.Таблица производных. Понятие сложной функции. Производная сложной функции. 17.Производные высших порядков. Физический смысл второй производной. 18.Первообразная. Неопределенный интеграл. Основные свойства неопределенного интеграла. 19.Таблица неопределенных интегралов. 20.Методы интегрирования: метод непосредственного интегрирования; метод замены переменной (метод подстановки); метод интегрирования по частям. 21.Определенный интеграл. Понятие интегральной суммы. Достаточное условие существования определенного интеграла (интегрируемости функции). 22.Основные свойства определенного интеграла. Геометрический смысл определенного интеграла. 23.Методы вычисления определенных интегралов. Формула Ньютона-Лейбница. 24.Геометрические и физические приложения определенного интеграла. 25.Понятие дифференциального уравнения. Общее и частное решение дифференциального уравнения. Интегральные кривые. Задача Коши. 26. Размещения. Перестановки. Сочетания. 27. Классическое определение вероятности. Теоремы сложения и умножения вероятности. 28. ДСВ. Вычисление числовых характеристик ДСВ. 29. НСВ. Функция и плотность распределения НСВ. Задания экзамена 1. Найдите производные следующих функций а) 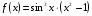 ; б) ; б) 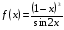 ; ; 2. Вычислите производную второго порядка: а) 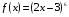 б) б) 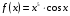 3. Решите уравнение 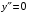 а) 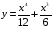 б) б) 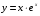 4. Вычислите неопределенный интеграл, используя непосредственное интегрирование: а)  ; б) ; б)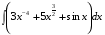 ; ;5. Вычислите неопределенный интеграл, используя метод замены переменной: а)  ; б) ; б) 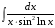 . .6. Вычислите неопределенный интеграл, используя метод интегрирования по частям: а)  ; ; 7. Вычислите: а)  ; б) ; б) 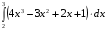 ; в) ; в) 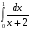 . .8. Найдите площадь фигуры, ограниченной линиями: а) 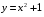 , , 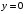 , , 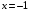 , , 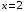 . . 9. Найдите объем тела, образованного вращением фигуры, ограниченной линиями:  , ,  , ,  , , 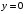 вокруг оси вокруг оси 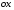 . .10. Найдите площадь фигуры, ограниченной линиями: а) 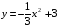 , , 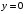 , , 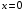 , , 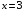 . . 11. Найдите объем тела, образованного вращением фигуры, ограниченной линиями: 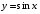 , , 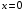 , , 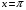 , , 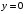 . .12.Проверьте подстановкой, что дифференциальное уравнение 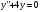 , имеет общим решением , имеет общим решением  . .13.Найдите общее решение уравнения: а) 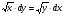 б) б) 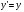
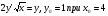 15.Найдите общее решение уравнения: 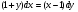 16. Найдите общее решение дифференциального уравнения: а) 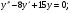 б) б) 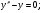 17. Найдите частное решение уравнения: а)    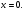 18.Выполните действия: 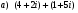 ; ;  ; ;  ; ; 19.Вычислите: 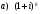 ; ; 20. Вычислите предел функции а) 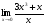 , д) , д) 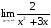 21. Вычислите предел функции с помощью правила Лопиталя. 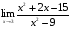 . .22. Вычислите предел функции а)  , , б) 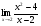 , ,в) 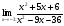 , ,23. Вычислите предел функции а)  , б) , б) 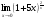 . .24. В партии из 24 деталей пять бракованных. Из партии выбирают наугад 6 деталей. Найти вероятность того, что среди этих 6 деталей окажутся 2 бракованных (событие 25. Дана интегральная функция F(x) распределения непрерывной случайной величины: 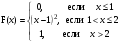 . . Требуется: 1) убедиться, что заданная функция F(x) является функцией распределения, проверив свойства функции; 2) найти плотность данного распределения f(x); 3) построить графики интегральной и дифференциальной функций распределения.
|
 .
.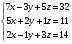 .
.