Урок геометрии в 7 классе по теме «Сумма углов треугольника»
 Скачать 80.5 Kb. Скачать 80.5 Kb.
|
| Урок геометрии в 7 классе по теме «Сумма углов треугольника» Учитель математики МБОУ Краснорогская ООШ Выгоничского района Курносова Наталья Николаевна. «Я слышу – я забываю, я вижу – я запоминаю, я делаю – я усваиваю» Китайская мудрость Как известно, в основе нынешней модернизации российского образования лежат идеи личностно-ориентированного развивающего обучения. Сегодня одна из важнейших задач общеобразовательной школы состоит уже не в том, чтобы «снабдить» учащихся багажом знаний, а в том, чтобы привить умения, позволяющие им самостоятельно добывать информацию и активно включаться в творческую, исследовательскую деятельность. В связи с этим актуальным становится внедрение в процесс обучения таких технологий, которые способствовали бы формированию и развитию у учащихся умения учиться, учиться творчески и самостоятельно. Основу концепции деятельностного подхода к обучению составляет положение: усвоение содержания обучения и развитие ученика происходит в процессе его собственной деятельности. Давно доказано психологами, что люди лучше усваивают то, что обсуждают с другими, а лучше всего помнят то, что объясняют другим. Тип урока: изучение нового материала. Цели урока: Образовательные:
Развивающие:
Воспитательные:
ход урока.
Приветствие. Проверка готовности учащихся к уроку. На доске тема урока и высказывание: …Как для смертных истина ясна, Что в треугольник двум тупым не влиться. Данте А.
Ребята, как вы думаете, о какой фигуре пойдет речь на этом уроке? Какие задачи урока? “открыть” и доказать теорему о сумме углов треугольника; научить решать задачи, применяя полученные знания.
Сформулируйте определение треугольника. (Треугольник это геометрическая фигура, образования тремя точками, не лежащими на одной прямой, и отрезками, попарно соединяющими эти точки.) Назовите элементы треугольника. (Углы, стороны, вершины.) Дайте названия треугольников по сторонам. (Равносторонний, равнобедренный, разносторонний.) Один из учащихся выбирает и показывает классу треугольники, заготовленные и лежащие на столе у учителя. 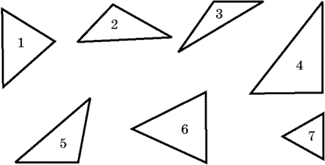 Треугольники различаются и по углам. Попробуем назвать треугольники по углам. (Другой учащийся выбирает: остроугольный, тупоугольный и прямоугольный треугольники.) Давайте ответим на ряд вопросов: Может ли треугольник иметь:
К доске вызывается один ученик и выполняет следующие рисунки: 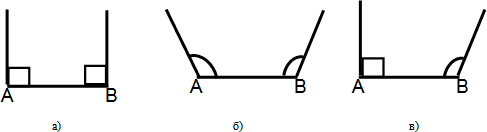 Далее идет «коллективное обсуждение». Построенные лучи не пересекаются, значит, треугольник не получится. Сумма односторонних углов в первом случае равна 180°, во втором и третьем случае больше, чем 180°. В первом случае прямые параллельны, а во втором и третьем случае прямые расходятся. Делаем вывод: треугольники не могут иметь два прямых, два тупых. А также в треугольнике не может быть одновременно один тупой и один прямой углы. Практическая работа (способствует актуализации знаний и навыков самопознания). У каждого из вас есть на парте по одному треугольнику разных цветов. Ребята, мы с вами измеряли углы и с помощью транспортира и находили их сумму еще в 5 классе. Сумма углов у всех получалась разная (так может получаться потому, что неточно приложили транспортир, небрежно выполнили подсчет и т.д.). Я предлагаю найти сумму углов треугольника двумя другими способами: возьмите треугольники, которые лежат у вас на парте. Они желтого или розового цвета. Обозначьте углы треугольника числами 1, 2, 3. Учащиеся с желтыми треугольниками: оторвите два угла треугольника и приложите их к сторонам третьего угла так, чтобы все вершины были в одной точке. Замечаем, что все углы треугольника в сумме образуют развернутый угол. Учащиеся с розовыми треугольниками: сложите углы во внутрь треугольника. Заметим, что перегибать треугольник надо по прямой параллельной к стороне, того угла который мы будем сгибать первым, а данный угол должен касаться данной стороны. Замечаем, что все углы треугольника в сумме образуют развернутый угол. Чему равна градусная мера развернутого угла? К какому выводу мы пришли? Сумма углов треугольника равна 180 градусов. Выполнив практическую работу, мы установили, что сумма углов треугольника равна 180 градусов. В математике практическая работа дает возможность лишь сделать какое-то утверждение, но его нужно доказать. Утверждение, справедливость которого устанавливается путем доказательства, называется теоремой. Какую теорему нам нужно доказать? Сумма углов треугольника равна 180 градусов.
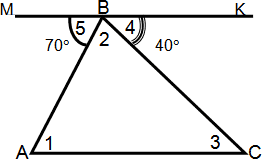
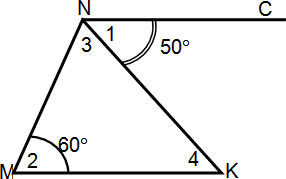
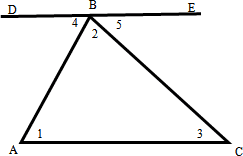
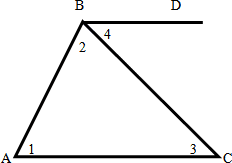
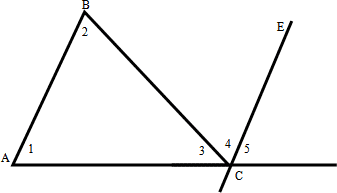
Прежде, чем доказать эту теорему решим две задачи устно они помогут нам при доказательстве теоремы:
VII. Закрепление изученного материала.Теперь, пользуясь теоремой, можно обосновать, почему в треугольнике не может быть двух прямых углов, двух тупых углов, двух углов, один из которых тупой, а другой прямой. Следствие из теоремы о сумме углов треугольника (выводится учащимися самостоятельно; это способствует развитию умения формулировать собственную точку зрения, высказывать и аргументировать ее). В любом треугольнике либо все углы острые, либо два острых угла, а третий тупой или прямой. Если в треугольнике все углы острые, то он называется остроугольным. Если один из углов треугольника тупой, то он называется тупоугольным. Если один из углов треугольника прямой, то он называется прямоугольным. Устная работа: (планшеты) Слайд 15. 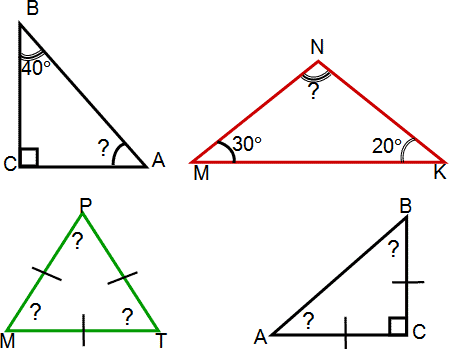 Графический диктант
Самопроверка Итак, ребята этот урок пополнил ваши знания о треугольнике, но это еще не предел. На следующих уроках мы продолжим изучение треугольников, и вы узнаете еще много интересного и познавательного об этой геометрической фигуре. IIX. Задание на дом.Пункт 30. № 223 (б), № 228 (а). IX. Итог урока.Рефлексия: Продолжите фразу:
|